用牛顿法求解代价函数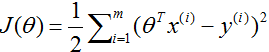
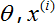
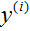
解 牛顿法（
详细点此）迭代公式为
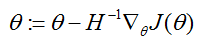
这里，
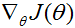
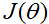
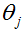
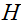
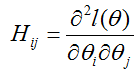
先求
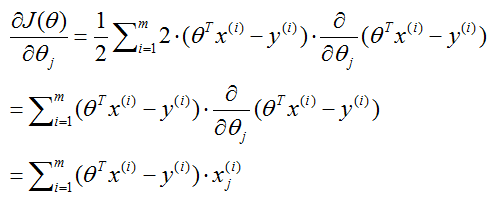
上式即为向量
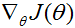
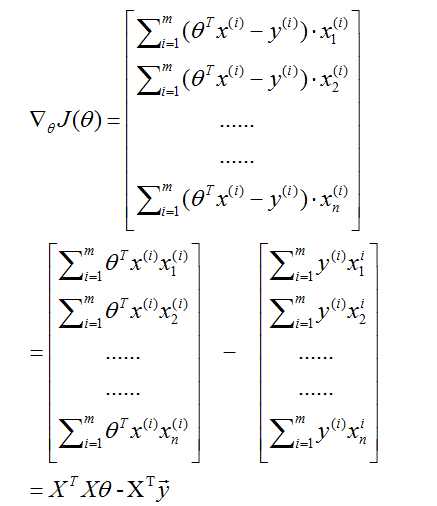
其中，
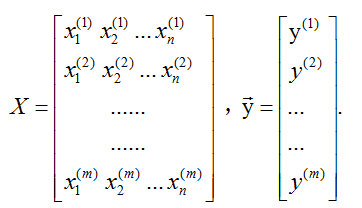
然后求解海森矩阵，
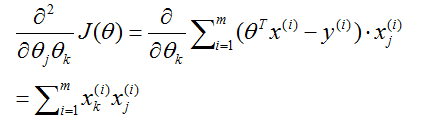
所以，
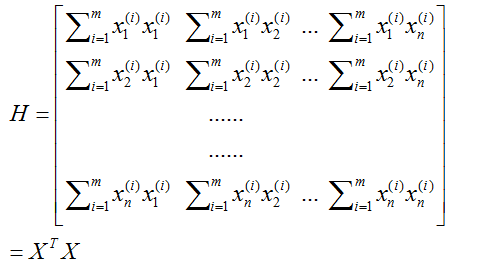
从而选择随机初始值
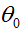
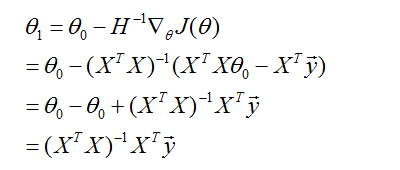
我们发现无论
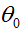
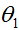
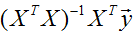
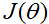
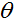
因此，牛顿法经过一步迭代，即可求解最小二乘问题。
最后
以上就是谨慎汽车最近收集整理的关于牛顿法求解最小二乘问题（线性回归）的全部内容，更多相关牛顿法求解最小二乘问题（线性回归）内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![[机器学习入门] 李宏毅机器学习笔记-3 （Gradient Descent ；梯度下降）Review梯度下降的三个小贴士](https://file2.kaopuke.com:8081/files_image/reation/bcimg9.png)
发表评论 取消回复