俯视机器学习

数学有多伤人，就有多销魂！

第9章 神经网络

1. 简介

模型术语：

• 神经元
• 输入（训练数据）
• 输出
• 激活函数
• 损失函数（交叉熵、平方误差）
• 权重（训练参数）

优化术语：

• 优化方法（优化器）：梯度下降法
• 学习步长

训练术语：

• batch size
• iteration
• epoch

模型特点：多个局部最小值

直观理解为什么 work。

2. 矩阵求导

逐元素函数：

如果 $\sigma (X)$ 是一个逐元素函数，则
$$\mathrm{d}\sigma (X)={\sigma }^{\prime }(X)\odot \mathrm{d}X$$
其中 $X$ 可以为向量或矩阵，${\sigma }^{\prime }$ 同样为逐元素函数，$\odot$ 代表逐元素相乘。例如
$$\sigma (h)=\frac{1}{1+e^{-h}}$$
其中 $\sigma$ 是一个逐元素函数，$h\in R^d$ 是一个 $d$ 维向量。则返回的 $\sigma (h)$ 也是一个 $n$ 维向量，且有 $\sigma (h{)}_i=\frac{1}{1+e^{-h_i}},i=1,\cdots ,d$ 。则
$$\mathrm{d}\sigma (h)=(\frac{1}{1+e^{-h}}{)}^{\prime }\mathrm{d}h=\frac{e^{-h}}{(1+e^{-h}{)}^2}\mathrm{d}h$$
注意区分逐元素函数与普通函数区别。逐元素函数可以把输入向量或矩阵的单独元素输入，返回一个值。而普通函数把向量或矩阵当作一个整体进行运算。

另外，$\sigma (x)=sigmoid(x)$ 函数有一个很好的性质，即：
$${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$$

3. 全连接神经网络公式推导

推导2层全连接前馈神经网络。输如 $x\in R^d$ ，两个隐藏层权重为 $W_1$ 、$W_2$ 。第1层和第2层输出分别为 $h_1$ 和 $h_2$ 。中间用 $sigmoid$ 函数，损失函数采用平方误差和，则
$$\begin{array}{rl}{h}_1& =W_{1}x\\ s_1& =\sigma (h_1)\\ h_2& =W_2{s}_1\\ l& =\frac{1}{2}\Vert h_2-y{\Vert }_2^2=\frac{1}{2}(h_2-y{)}^T(h_2-y)\end{array}$$

整个推导想要的结果为：
$$\frac{\partial l}{\partial W_1},\frac{\partial l}{\partial W_2}$$

(1)
$$\begin{array}{rl}dl& =d{h}_2^T(h_2-y)+(h_2-y{)}^{T}d{h}_2\\ tr(dl)& =tr((h_2-y{)}^{T}d{h}_2)\\ \frac{\partial l}{\partial h_2}& =h_2-y\end{array}$$
(2)
$$\begin{array}{rl}dl& =tr({\frac{\partial l}{\partial h_2}}^{T}d{h}_2)\\ & =tr\left({\frac{\partial l}{\partial h_2}}^{T}d(W_2{s}_1)\right)\\ & =tr\left({\frac{\partial l}{\partial h_2}}^{T}d{W}_2{s}_1\right)+tr\left({\frac{\partial l}{\partial h_2}}^T{W}_{2}d{s}_1\right)\\ \frac{\partial l}{\partial W_2}& =\frac{\partial l}{\partial h_2}{s}_1^T\\ \frac{\partial l}{\partial s_1}& =W_2^T\frac{\partial l}{\partial h_2}\end{array}$$

(3)
$$\begin{array}{rl}tr\left({\frac{\partial l}{\partial s_1}}^{T}d{s}_1\right)& =tr\left({\frac{\partial l}{\partial s_1}}^{T}d\sigma (h_1)\right)\\ & =tr\left({\frac{\partial l}{\partial s_1}}^T[{\sigma }^{\prime }(h_1)\odot d{h}_1]\right)\\ & =tr\left([\frac{\partial l}{\partial s_1}\odot {\sigma }^{\prime }(h_1){]}^{T}d{h}_1\right)\\ \frac{\partial l}{\partial h_1}& =\frac{\partial l}{\partial s_1}\odot {\sigma }^{\prime }(h_1)=\frac{\partial l}{\partial s_1}\odot [\sigma (h_1)\odot (1-\sigma (h_1))]\end{array}$$

(4)
$$\begin{array}{rl}dl& =tr({\frac{\partial l}{\partial h_1}}^{T}d{h}_1)\\ & =tr\left({\frac{\partial l}{\partial h_1}}^{T}d(W_{1}x)\right)\\ & =tr\left({\frac{\partial l}{\partial h_1}}^{T}d{W}_{1}x\right)\\ \frac{\partial l}{\partial W_1}& =\frac{\partial l}{\partial h_1}{x}^T\end{array}$$

如果损失函数取交叉熵,参考此处，则
$$l=-y^T\log \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(h_2)$$
其中 $\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}$ 函数的定义为对向量 $z\in R^n$
$$[\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(z){]}_i=\frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}$$
最终获得的结果也为一个 $n$ 维向量。

则
$$\frac{\partial l}{\partial h_2}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(h_2)-y$$

4. 实战：手写数字识别（2层全连接网络）

数据集介绍：

• 数据来源：E. Alpaydin, C. Kaynak
• 5000+图片，每张大小为 $8\times 8$ ，拉成一维列表，故得 64 个特征。本次实战只采用 100 个数字，0-9 每个数字 10 个。
• 目标：根据输入的图片，对数字进行分类。

import numpy as np
import pandas as pd
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1./(1 + np.exp(-x))

def softmax(x):
    return np.exp(x) / np.exp(x).sum()

def onehot(y, n):
    yy = np.zeros(n)
    yy[y] = 1.
    return yy.reshape(-1, 1)


X, y = load_digits(return_X_y=True)
X = X[:100]  # 只取前面100个数字测试，0-9每个数字10个
y = y[:100]

N = 128
nClass = 10
eta = 1e-3
epoch = 4

W1 = np.random.randn(N, X.shape[1])
W2 = np.random.randn(nClass, N)

loss = []
for e in range(20):
    lss = []
    for _ in range(1000):
        i = np.random.choice(np.arange(len(X)))
        x = X[i, :].reshape(-1, 1)     # 变成列向量
        yi = onehot(y[i], nClass)      # 变成列向量
        # 正向计算
        h1 = (W1 @ x).reshape(-1, 1)
        s1 = sigmoid(h1)
        h2 = (W2 @ s1).reshape(-1, 1)
        ls = -yi.T @ np.log(softmax(h2))
        lss.append(ls[0,0])
        # 反向传播
        plph2 = h2 - yi
        plpW2 = plph2 * s1.T 
        plps1 = W2.T @ plph2 
        plph1 = plps1 * (sigmoid(h1) * (1 - sigmoid(h1)))
        plpW1 = plph1 @ x.T
        # 更新权重
        W1 -= eta * plpW1
        W2 -= eta * plpW2
    loss.append(np.mean(lss))   
    eta *= 0.6

# 准确率
H1 = (W1 @ X.T)
S1 = sigmoid(H1)
H2 = (W2 @ S1)
# acc
acc = np.sum(H2.argmax(axis=0) == y) / len(y)
print(f'Accurancy = {acc}')

# 绘图
plt.plot(loss)
plt.show()

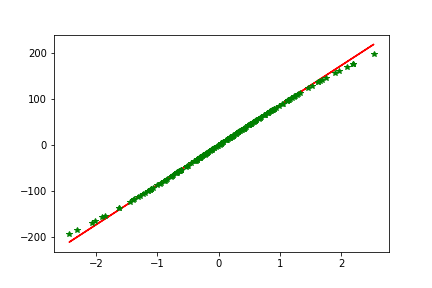
5. 实战：神经网络回归问题

X, y = make_regression(n_samples=200, n_features=1, random_state=1)

N = 128
eta = 0.003
epoch = 200

W1 = np.random.randn(N, X.shape[1])
W2 = np.random.randn(1, N)

loss = []
for e in range(epoch):
    lss = []
    for i in range(len(X)):
        x = X[i, :].reshape(-1, 1) # 变成列向量
        yi = np.array([y[i]])      # 变成列向量
        # 正向计算
        h1 = (W1 @ x).reshape(-1, 1)
        s1 = sigmoid(h1)
        h2 = (W2 @ s1).reshape(-1, 1)
        
        ls = np.linalg.norm(h2.ravel() - yi)
        lss.append(ls)
        # 反向传播
        plph2 = h2 - yi
        plpW2 = plph2 * s1.T #+ 0.0001 * W2
        plps1 = W2.T @ plph2        
        plph1 = plps1 * (sigmoid(h1) * (1 - sigmoid(h1)))
        plpW1 = plph1 @ x.T  #+ 0.0001 * W1
        # 更新权重
        W1 -= eta * plpW1
        W2 -= eta * plpW2
    
    loss.append(np.mean(lss))
#     if e % 10 == 0:
#         print(np.linalg.norm(W1, 'fro'))


H1 = (W1 @ X.T)
S1 = sigmoid(H1)
H2 = (W2 @ S1)
# 绘图
plt.plot(X.ravel(), y, 'r', X.ravel(), H2.ravel(), 'g*')
plt.show()

6. Sklearn 中的神经网络

class sklearn.neural_network.MLPRegressor(hidden_layer_sizes=(100, ), activation=’relu’, *, solver=’adam’, alpha=0.0001,batch_size=’auto’, learning_rate=’constant’, learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True,early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)

• 参数
  • hidden_layer_sizes [tuple, length = n_layers - 2, default=(100,)] 隐藏层
  • activation [{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, default=’relu’] 激活函数
  • batch_size [int, default=’auto’] 批处理数据量
  • learning_rate [{‘constant’, ‘invscaling’, ‘adaptive’}, default=’constant’] 学习率
  • learning_rate_init [double, default=0.001] 学习率初始值
  • max_iter [int, default=200] 最大迭代次数
  • shuffle [bool, default=True] 是否打乱每次迭代的样本顺序
• 属性
  • loss_ [float] 损失
  • coefs_ [list, length n_layers - 1] 系数
  • intercepts_ [list, length n_layers - 1] 截距
• 方法
  • fit(X, y)
  • predict(X)
  • score(X, y[, sample_weight])

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits, make_regression
from sklearn.neural_network import MLPClassifier, MLPRegressor

# 分类
X, y = load_digits(return_X_y=True)
X = X[:100]  # 只取前面100个数字测试，0-9每个数字10个
y = y[:100]

clf = MLPClassifier((128,)).fit(X, y)
clf.score(X, y)

# 回归
X, y = make_regression(n_samples=200, n_features=1, random_state=1)
print(X.shape)

clf = MLPRegressor((128,), max_iter=200, learning_rate_init=0.2).fit(X, y)
ypred = clf.predict(X)

plt.plot(X.ravel(), y, 'r', X.ravel(), ypred, 'g*')
plt.show()

版权申明：本教程版权归创作人所有，未经许可，谢绝转载！

交流讨论QQ群：784117704

部分视频观看地址：b站搜索“火力教育”

课件下载地址：QQ群文件（有最新更新） or 百度网盘PDF课件及代码

链接：https://pan.baidu.com/s/1lc8c7yDc30KY1L_ehJAfDg
提取码：u3ls

最后

以上就是聪慧吐司为你收集整理的第9章 BP神经网络（算法原理+手编实现+库调用） 俯视机器学习 第9章 神经网络的全部内容，希望文章能够帮你解决第9章 BP神经网络（算法原理+手编实现+库调用） 俯视机器学习 第9章 神经网络所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。