用python处理时间序列数据,检验平稳性跟纯随机性
from statsmodels.tsa.stattools import adfuller as adf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import pandas as pd
import numpy as np
!pip install statsmodels
Requirement already satisfied: statsmodels in c:programdataanaconda3libsite-packages (0.11.0)
Requirement already satisfied: numpy>=1.14 in c:programdataanaconda3libsite-packages (from statsmodels) (1.18.1)
Requirement already satisfied: scipy>=1.0 in c:programdataanaconda3libsite-packages (from statsmodels) (1.4.1)
Requirement already satisfied: pandas>=0.21 in c:programdataanaconda3libsite-packages (from statsmodels) (1.0.1)
Requirement already satisfied: patsy>=0.5 in c:programdataanaconda3libsite-packages (from statsmodels) (0.5.1)
Requirement already satisfied: pytz>=2017.2 in c:programdataanaconda3libsite-packages (from pandas>=0.21->statsmodels) (2019.3)
Requirement already satisfied: python-dateutil>=2.6.1 in c:programdataanaconda3libsite-packages (from pandas>=0.21->statsmodels) (2.8.1)
Requirement already satisfied: six in c:programdataanaconda3libsite-packages (from patsy>=0.5->statsmodels) (1.14.0)
data=pd.read_excel('./data.xls',encoding='utf-8')
data
| time | wc(误差随机项) | xt1 | xt2 | xt3 | |
|---|---|---|---|---|---|
| 0 | 1 | 1.74 | 1.000000 | 1.000 | 1.000 |
| 1 | 2 | -0.70 | 0.800000 | 0.800 | 0.800 |
| 2 | 3 | -1.28 | 2.650000 | 1.440 | 1.430 |
| 3 | 4 | 0.43 | 7.440000 | 5.094 | 4.060 |
| 4 | 5 | 0.24 | 13.804000 | 10.204 | 5.645 |
| ... | ... | ... | ... | ... | ... |
| 95 | 96 | 1.55 | 739.086685 | 6908.698 | 146.490 |
| 96 | 97 | 0.07 | 748.322011 | 7056.498 | 147.345 |
| 97 | 98 | -0.73 | 756.383207 | 7205.072 | 148.140 |
| 98 | 99 | 0.66 | 765.129924 | 7356.450 | 150.725 |
| 99 | 100 | -0.44 | 773.187954 | 7508.420 | 151.515 |
100 rows × 5 columns
对X1做平稳性检验
xt1=data.xt1
dftest=adf(xt1)
pd.Series(dftest[0:4],index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
#p值高达0.9几
Test Statistic 0.678947
p-value 0.989408
#Lags Used 1.000000
Number of Observations Used 98.000000
dtype: float64
xt1.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x238faff6208>
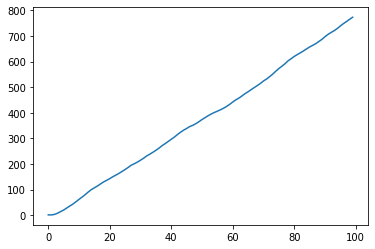
[output_6_1.png)]
#一阶差分
xt1_1 = xt1.diff(1)
xt1_1.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x238fa6a5048>
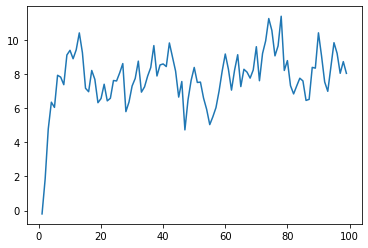
[(output_7_1.png)]
#一阶差分的单位根检验
dftest_1 = adf(xt1_1.dropna())
pd.Series(dftest_1[0:4],index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
#一阶差分后p值小于0.05,拒绝原假设(即不存在单位根,认为其已经平稳)
Test Statistic -6.056515e+00
p-value 1.241430e-07
#Lags Used 0.000000e+00
Number of Observations Used 9.800000e+01
dtype: float64
dftest_1[1]-0.05
-0.049999875856979056
#画一阶差分之后的自相关图跟偏自相关图
plot_acf(xt1_1.dropna())
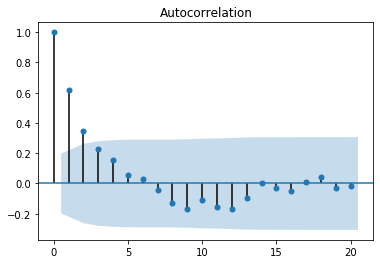
[(output_10_0.png)]
plot_pacf(xt1_1.dropna())
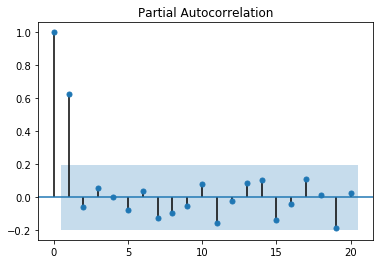
[(output_11_0.png)]
X2做平稳性检验
data.xt2.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x238fe204d88>
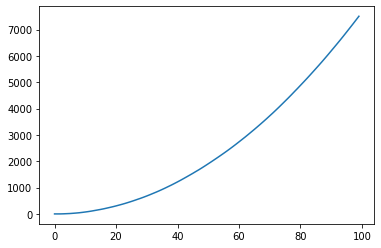
(output_13_1.png)]
#做二阶差分
x2_2=data.Xt2一阶差分.diff(1)
x2_2.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x238fc1d7a48>
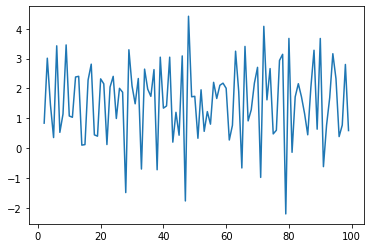
[output_14_1.png)]
#对二阶差分后的Xt2做单位根检验
adf(x2_2.dropna())
#故拒绝原假设,该序列平稳
(-7.1910449486700525,
2.5032477359463947e-10,
4,
93,
{'1%': -3.502704609582561,
'5%': -2.8931578098779522,
'10%': -2.583636712914788},
260.6359245108364)
#画二阶差分后的Xt2的自相关图跟偏自相关图
plot_acf(x2_2.dropna())
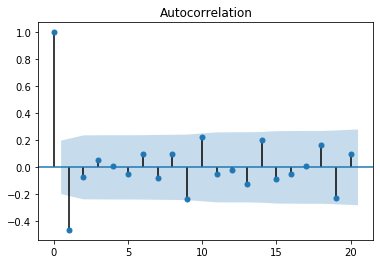
(output_16_0.png)]
plot_pacf(x2_2.dropna())
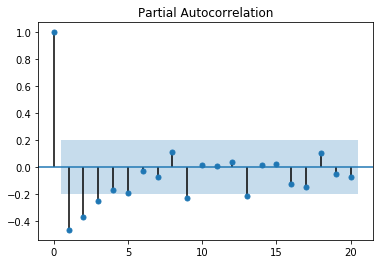
(output_17_1.png)]
对X3做平稳性检验
data.xt3.plot()
<matplotlib.axes._subplots.AxesSubplot at 0x238fd5efc08>
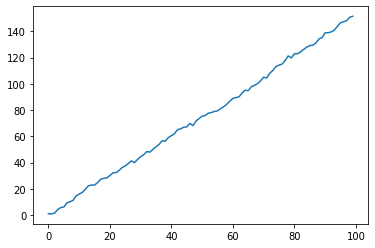
(output_19_1.png)]
#做一阶差分
data.xt3.diff(1).plot()
<matplotlib.axes._subplots.AxesSubplot at 0x238ff5dac88>
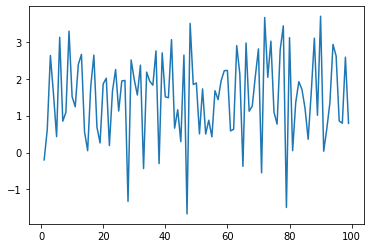
(output_20_1.png)]
#对一阶差分后的序列做单位根检验
adf(data.xt3.diff(1).dropna())
(-10.661639595719135,
4.391819453885797e-19,
1,
97,
{'1%': -3.4996365338407074,
'5%': -2.8918307730370025,
'10%': -2.5829283377617176},
257.9188344687909)
adf(data.xt3.diff(1).dropna())[1]-0.05
#故拒绝原假设,该序列平稳
-0.05
#对一阶差分后的Xt3画出自相关图跟偏自相关图
plot_acf(data.xt3.diff(1).dropna())
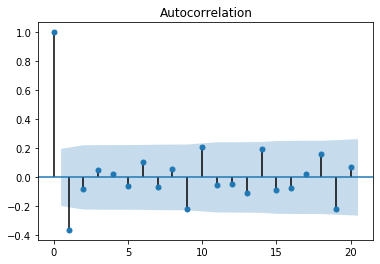
(output_23_1.png)]
plot_pacf(data.xt3.diff(1).dropna())
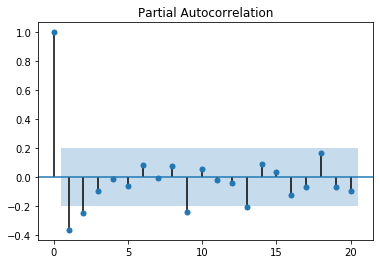
(output_24_1.png)]
最后
以上就是冷傲薯片最近收集整理的关于用python处理时间序列数据,检验平稳性跟纯随机性的全部内容,更多相关用python处理时间序列数据内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复