突变点检测：Mann-Kendall突变点检测（python）

不废话，直接上python代码

# Mann-Kendall突变点检测
# 数据序列y
# 结果序列UF，UB
#--------------------------------------------


import numpy as np
import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号


def Kendall_change_point_detection(inputdata):
    inputdata = np.array(inputdata)
    n=inputdata.shape[0]
    # 正序列计算---------------------------------
    # 定义累计量序列Sk，初始值=0
    Sk             = [0]
    # 定义统计量UFk，初始值 =0
    UFk            = [0]
    # 定义Sk序列元素s，初始值 =0
    s              =  0
    Exp_value      = [0]
    Var_value      = [0]
    # i从1开始，因为根据统计量UFk公式，i=0时，Sk(0)、E(0)、Var(0)均为0
    # 此时UFk无意义，因此公式中，令UFk(0)=0
    for i in range(1,n):
        for j in range(i):
            if inputdata[i] > inputdata[j]:
                s = s+1
            else:
                s = s+0
        Sk.append(s)
        Exp_value.append((i+1)*(i+2)/4 )                     # Sk[i]的均值
        Var_value.append((i+1)*i*(2*(i+1)+5)/72 )            # Sk[i]的方差
        UFk.append((Sk[i]-Exp_value[i])/np.sqrt(Var_value[i]))
    # ------------------------------正序列计算
    # 逆序列计算---------------------------------
    # 定义逆序累计量序列Sk2，长度与inputdata一致，初始值=0
    Sk2             = [0]
    # 定义逆序统计量UBk，长度与inputdata一致，初始值=0
    UBk             = [0]
    UBk2            = [0]
    # s归0
    s2              =  0
    Exp_value2      = [0]
    Var_value2      = [0]
    # 按时间序列逆转样本y
    inputdataT = list(reversed(inputdata))
    # i从2开始，因为根据统计量UBk公式，i=1时，Sk2(1)、E(1)、Var(1)均为0
    # 此时UBk无意义，因此公式中，令UBk(1)=0
    for i in range(1,n):
        for j in range(i):
            if inputdataT[i] > inputdataT[j]:
                s2 = s2+1
            else:
                s2 = s2+0
        Sk2.append(s2)
        Exp_value2.append((i+1)*(i+2)/4 )                     # Sk[i]的均值
        Var_value2.append((i+1)*i*(2*(i+1)+5)/72 )            # Sk[i]的方差
        UBk.append((Sk2[i]-Exp_value2[i])/np.sqrt(Var_value2[i]))
        UBk2.append(-UBk[i])
    # 由于对逆序序列的累计量Sk2的构建中，依然用的是累加法，即后者大于前者时s加1，
    # 则s的大小表征了一种上升的趋势的大小，而序列逆序以后，应当表现出与原序列相反
    # 的趋势表现，因此，用累加法统计Sk2序列，统计量公式(S(i)-E(i))/sqrt(Var(i))
    #也不应改变，但统计量UBk应取相反数以表征正确的逆序序列的趋势
    #  UBk(i)=0-(Sk2(i)-E)/sqrt(Var)
    # ------------------------------逆序列计算
    # 此时上一步的到UBk表现的是逆序列在逆序时间上的趋势统计量
    # 与UFk做图寻找突变点时，2条曲线应具有同样的时间轴，因此
    # 再按时间序列逆转结果统计量UBk，得到时间正序的UBkT，
    UBkT = list(reversed(UBk2))
    diff = np.array(UFk) - np.array(UBkT)
    K    = list()
    # 找出交叉点
    for k in range(1,n):
        if diff[k-1]*diff[k]<0:
            K.append(k)
    # 做突变检测图时，使用UFk和UBkT
    plt.figure(figsize=(10,5))
    plt.plot(range(1,n+1) ,UFk  ,label='UFk') # UFk
    plt.plot(range(1,n+1) ,UBkT ,label='UBk') # UBk
    plt.ylabel('UFk-UBk')
    x_lim = plt.xlim()
    plt.plot(x_lim,[-1.96,-1.96],'m--',color='r')
    plt.plot(x_lim,[  0  ,  0  ],'m--')
    plt.plot(x_lim,[+1.96,+1.96],'m--',color='r')
    plt.legend(loc=2) # 图例
    plt.show()
    return K

测试(下面对照了其他突变方法，下文讲)：

dt = [15.4,14.6,15.8,14.8,15.0,15.1,15.1,15.0,15.2,15.4,
      14.8,15.0,15.1,14.7,16.0,15.7,15.4,14.5,15.1,15.3,
      15.5,15.1,15.6,15.1,15.1,14.9,15.5,15.3,15.3,15.4,
      15.7,15.2,15.5,15.5,15.6,15.1,15.1,16.0,16.0,16.8,
      16.2,16.2,16.0,15.6,15.9,16.2,16.7,15.8,16.2,15.9,
      15.8,15.5,15.9,16.8,15.5,15.8,15.0,14.9,15.3,16.0,
      16.1,16.5,15.5,15.6,16.1,15.6,16.0,15.4,15.5,15.2,
      15.4,15.6,15.1,15.8,15.5,16.0,15.2,15.8,16.2,16.2,
      15.2,15.7,16.0,16.0,15.7,15.9,15.7,16.7,15.3,16.1,16.2]
plt.plot(dt)
plt.plot([0,35],[np.mean(dt[0:36]),np.mean(dt[0:36])],'m--',color='r')
plt.plot([37,90],[np.mean(dt[37:]),np.mean(dt[37:])],'m--',color='r')

plt.plot([0,32],[np.mean(dt[0:33]),np.mean(dt[0:33])],'o--',color='orange')
plt.plot([34,68],[np.mean(dt[34:69]),np.mean(dt[34:69])],'o--',color='orange')
plt.plot([70,90],[np.mean(dt[70:]),np.mean(dt[70:])],'o--',color='orange')
print("Mann-Kendall:",Kendall_change_point_detection(dt))
print("Pettitt:",Pettitt_change_point_detection(dt))
print("Buishand U Test:",Buishand_U_change_point_detection(dt))
print("Standard Normal Homogeneity Test (SNHT):",SNHT_change_point_detection(dt))

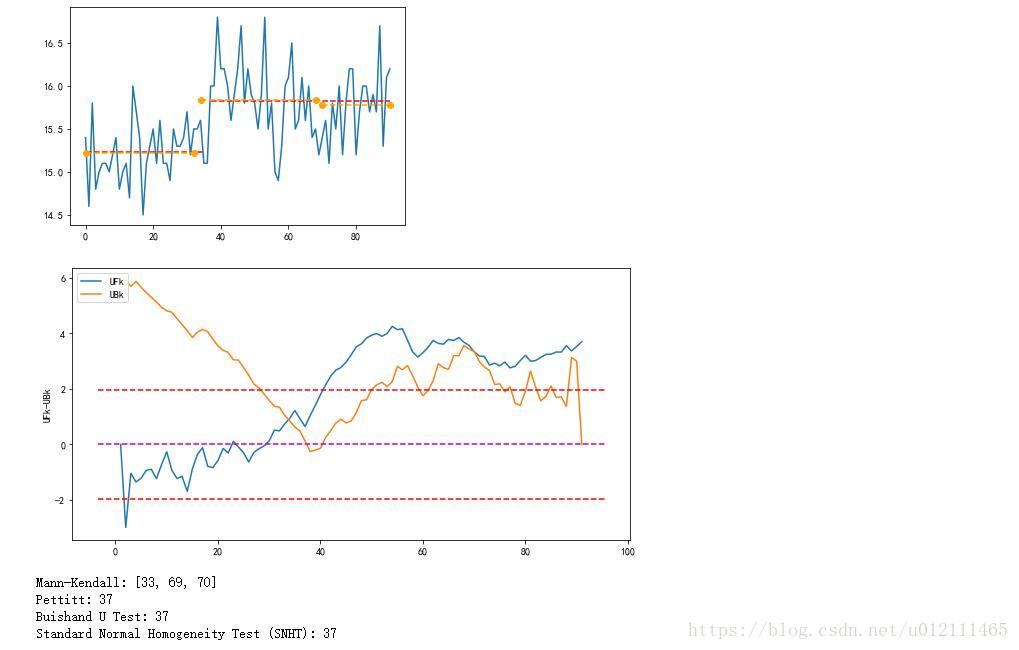
最后

以上就是标致小丸子为你收集整理的突变点检测：Mann-Kendall突变点检测（python）的全部内容，希望文章能够帮你解决突变点检测：Mann-Kendall突变点检测（python）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。