发现一个参数方程

157 阅读 0 评论 104 点赞

我是靠谱客的博主难过冷风，这篇文章主要介绍发现一个参数方程，现在分享给大家，希望可以做个参考。

犹豫了很久，只是出于好奇的目的，还是把它公布出来吧。

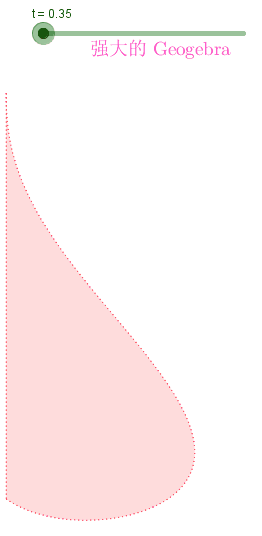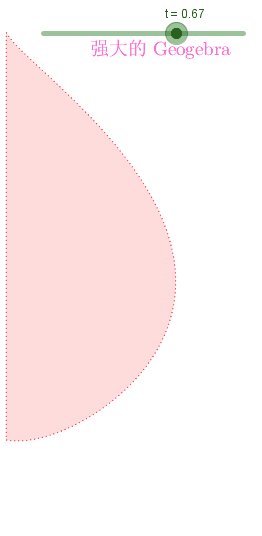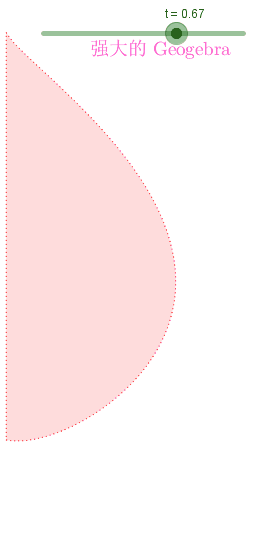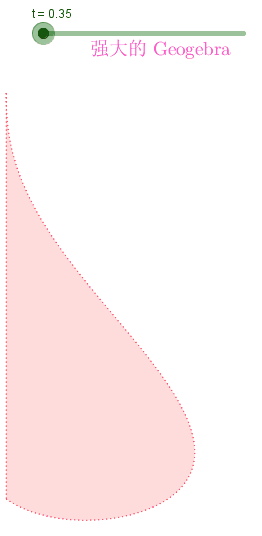
⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ x y = = 2.10526 (0.5275 - 0.15 t) cos s \cdot sin s \cdot ln | s | t - 0.2375 3 - | s | t cos s - - - - \sqrt

其中 s∈[−1,0] 是曲线长度相关的参数； t∈[0.35,0.82] 是表达曲线形状变化的时间参数的变量。

从而可以动态表示为：

lb=0.35;ub=0.825;α=0.85;
list=Table[ParametricPlot[{((ub-α lb-(1-α)b)/(ub-lb))Sin@t Cos@t Log@Abs@t ,(b-(ub-lb)/2)/3-(Abs@t)^b Sqrt[Cos@t]},{t,-1,0},Axes->None,Frame->None,PlotPoints->150,PlotRange->{{0,0.35},{-0.81,(ub-lb)/2.65}},ImageSize->300,AspectRatio->2.3]/.Line[l_List]:>{Directive[EdgeForm[Opacity[1,Red]],Opacity[0.2,Red]],Polygon[l]},{b,lb,ub,(ub-lb)/14}];
ListAnimate[#,DefaultDuration->1]&@Join[list[[1;;-2]],Reverse@list]