

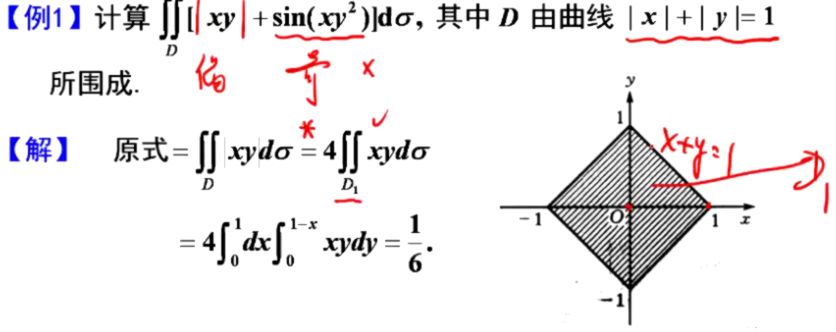
1.直角坐标求二重积分
2.极坐标求二重积分
可利用对称性加快解题速度
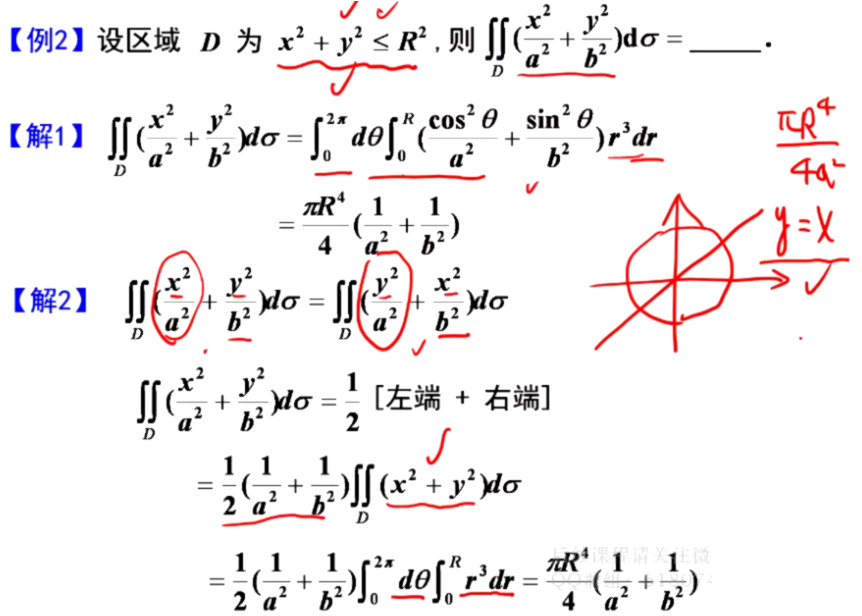
技巧:排除法,将参数取一个特殊值,进行带入计算。

利用函数奇偶性,可以判断函数的区域积分是否为0,减少计算量

利用平移巧做积分

2007年真题

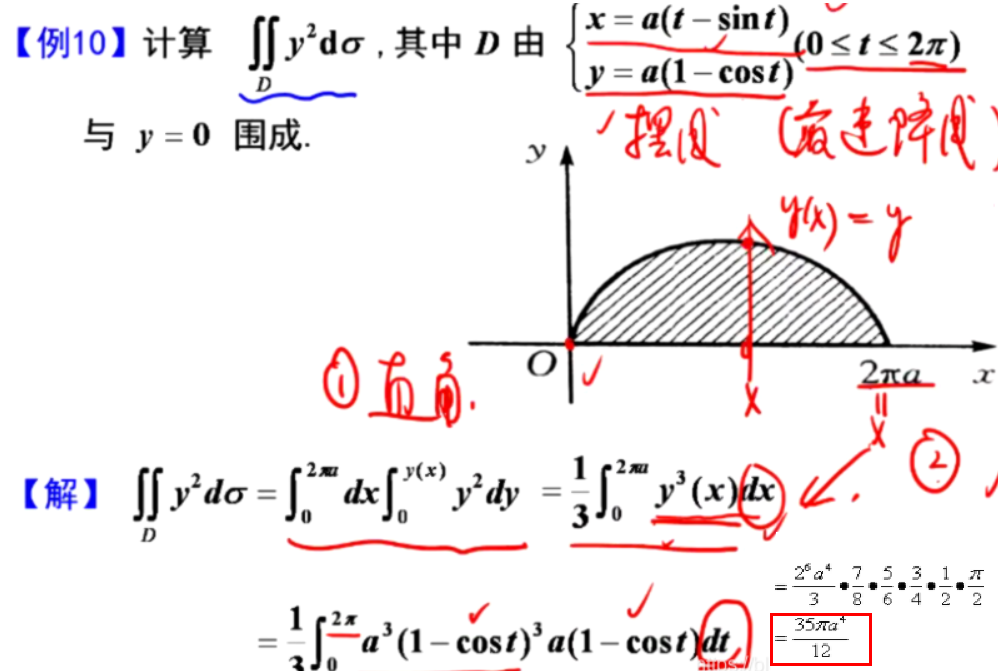
参数方程问题
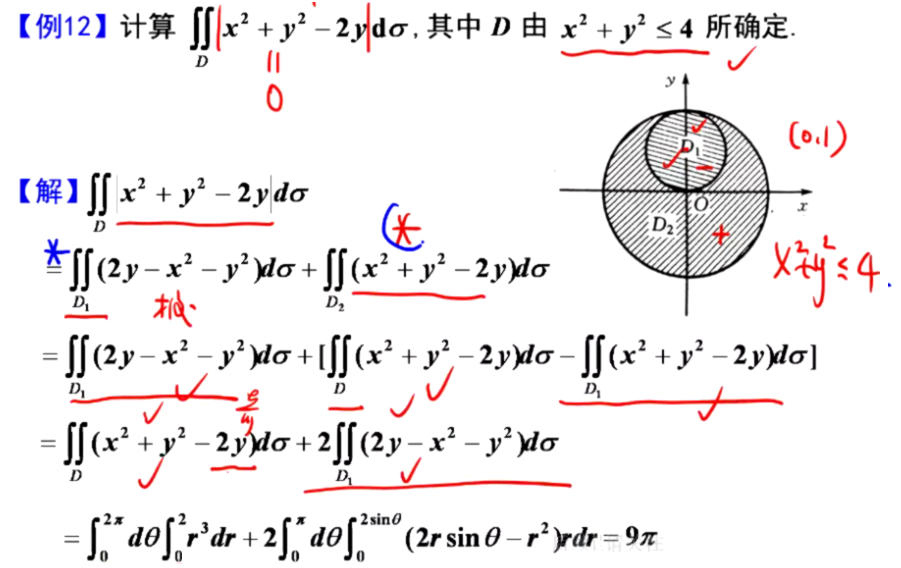
确定被积函数的正负号
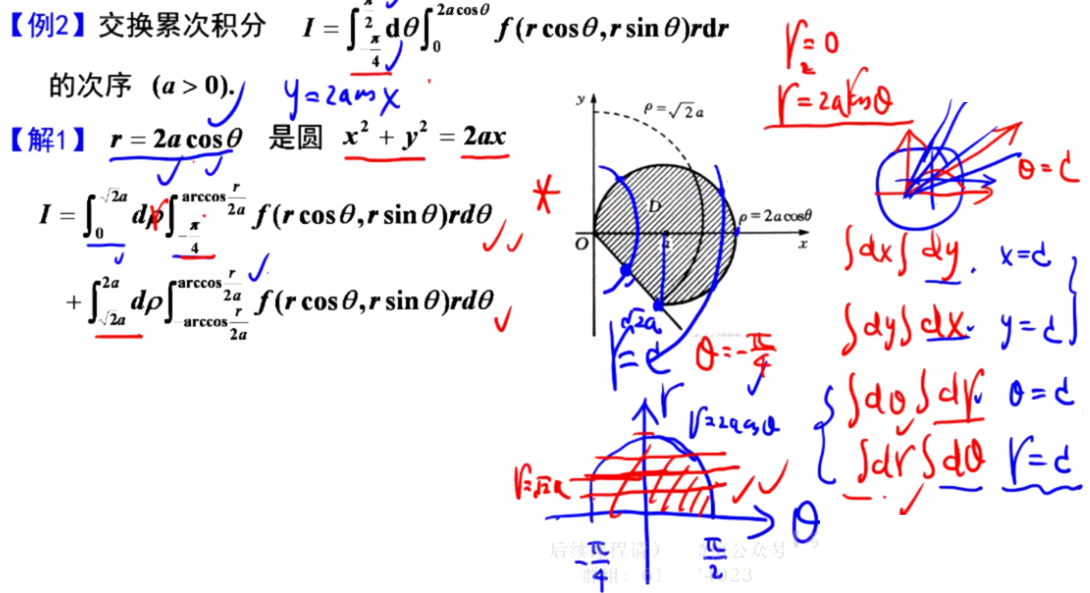
3.直角坐标交换积分次序
注意有的时候要变号

4.极坐标交换次序
将直角坐标和极坐标的方法联系起来。
证明题
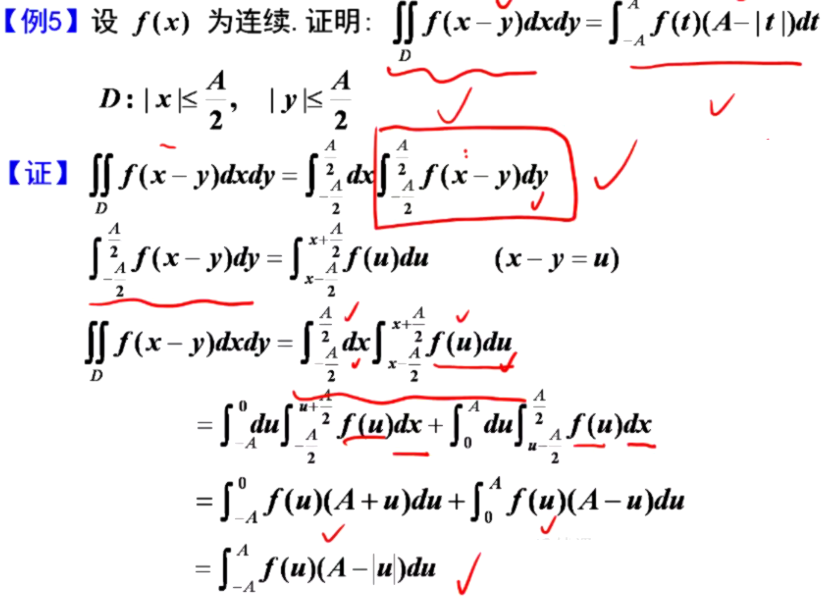
5.二重积分和微分方程综合题

6.二重积分与求极限综合
一般解法:变换积分次序,然后洛必达,积分中值定理
特殊解法:二重积分中值定理
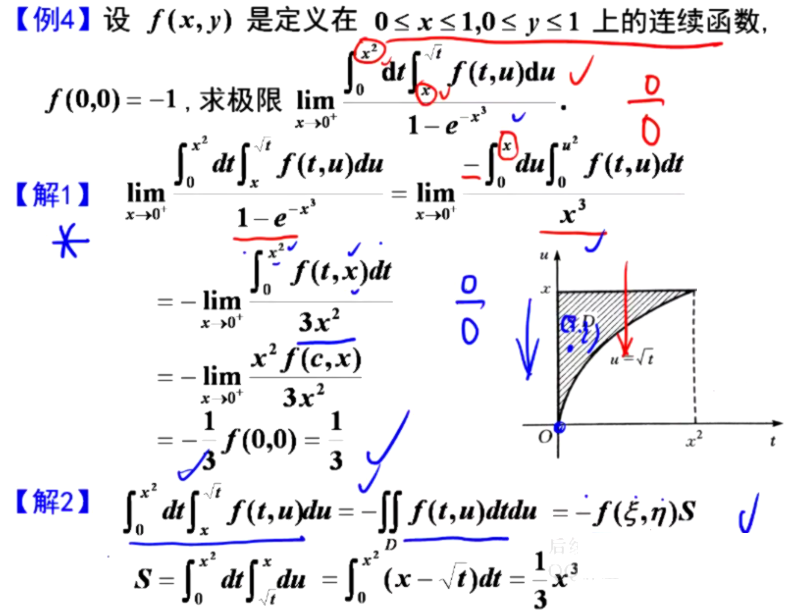
微分、重积分、中值定理综合题

7.二重积分复杂证明题
证1:利用分部积分思想,凑出二阶偏导
证2:利用微分思想,拉格朗日中值定理

8.二重积分比大小
被积函数一样,比较区域大小。
区域一样,比较被积函数大小。
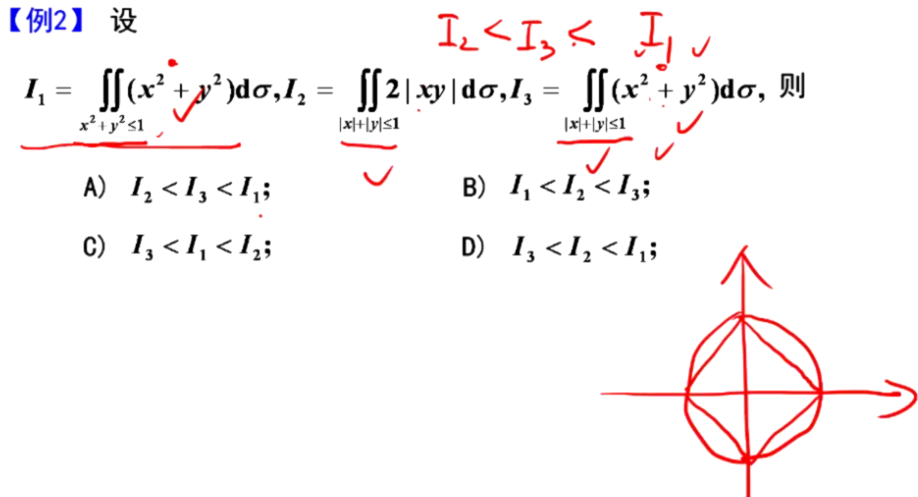
不等式证明,遇到乘积要考虑将一元积分变为二重积分
也可以用柯西积分不等式解题:
∫
f
2
(
x
)
d
x
∫
g
2
(
x
)
d
x
≥
(
∫
f
(
x
)
g
(
x
)
d
x
)
2
int f^2(x)dxint g^2(x)dxge (int f(x)g(x)dx)^2
∫f2(x)dx∫g2(x)dx≥(∫f(x)g(x)dx)2

遇到乘积,考虑化一重为二重积分

最后
以上就是哭泣白开水最近收集整理的关于高等数学强化6:二重积分的全部内容,更多相关高等数学强化6内容请搜索靠谱客的其他文章。








发表评论 取消回复