多元积分
0、preface
多元积分的主要内容包含了三点:
1、基本概念
2、计算
3、应用
整体内容相当于将一元积分进行了维度的推广——从二维空间推广到更高维度。多元积分成功地将一元函数的一重积分推广到二重三重,此外还添加了曲线曲面积分。曲线曲面积分又可以分别分为第一类和第二类。
从定义上来讲,一元积分和多元积分没有什么区别,都是和式的极限。从计算上来看,除了将多元积分转换成重积分之外,更重要的思想是进行各种变换——极坐标、参数方程、柱坐标、球坐标等。这样的转换有着显著的特征,可以在看到题目时根据题目特征进行合适的转换。此外,在进行曲线曲面积分时,格林公式、高斯公式和斯托克斯公式这三大公式可以带来简便。基于多元函数的定义,可以利用此函数对一些几何量(平面的面积、曲面的面积、空间几何体的体积、曲线的弧长)和物理量(质量、质心、形心、功、转动惯量、引力、流量)进行建模计算。
1、基本概念
1.1、基本概念综述
多元积分大致可以分为重积分和曲线曲面积分两种。根据下方的思维导图的分析,大致可以窥知一二。
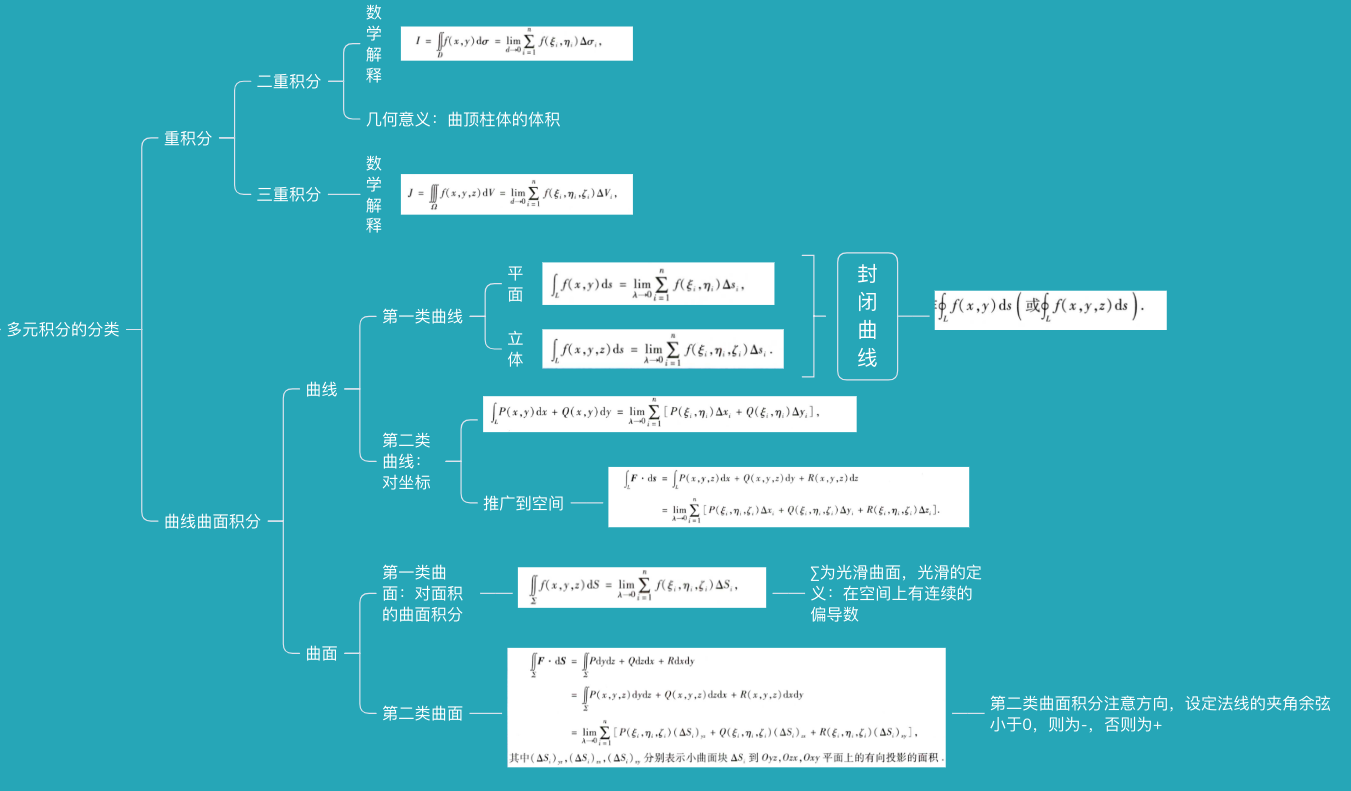
上述各种积分的意义大致一样,即积分区域被划分成无穷多个小区域之后再累积求极限。不同的是划分区域的方法。第二类曲面曲线积分的区域皆为投影所得,二第一类曲面曲线和二重三重积分的小区域皆为实际存在的空间划分。
1.2、多元(二重)积分的性质
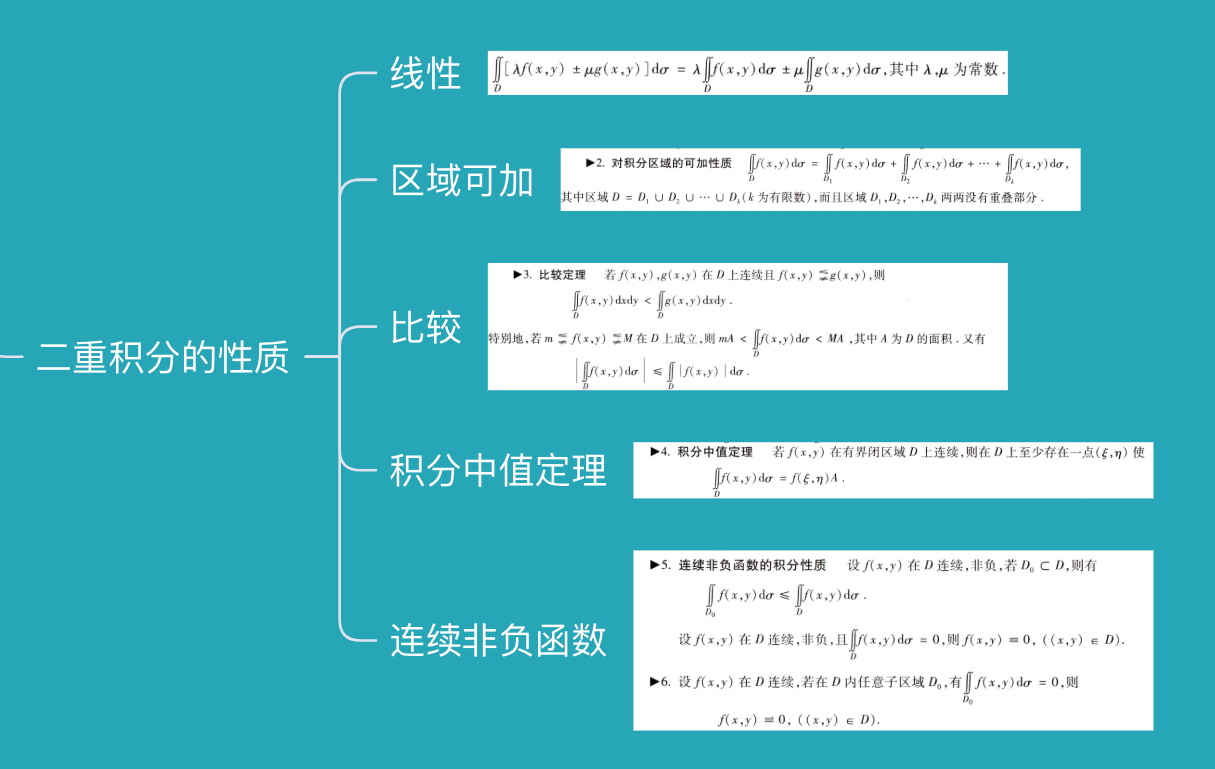
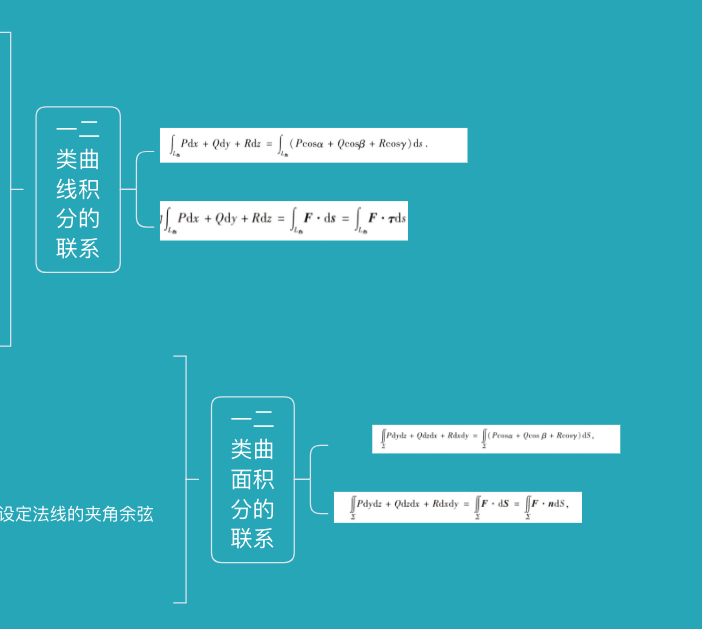
注意第二类曲线曲面积分存在方向的关系,即第二类需要考虑曲线方向/投影方向的正负关系。

由于第二类曲线曲面积分本质上是求投影在某个面/线上的值,以下特殊情况在具体计算中可以用到,即凑出积分值为0的第二类曲线曲面积分的情况:

2、计算
计算是二重积分的的大头,具体的计算方法分为按照概念计算、按照几何意义计算、按照特殊公式计算等。
2.1 按照概念计算
2.1.1 曲线积分化为定积分
(1)基于参数方程,第一类曲线积分的求法:
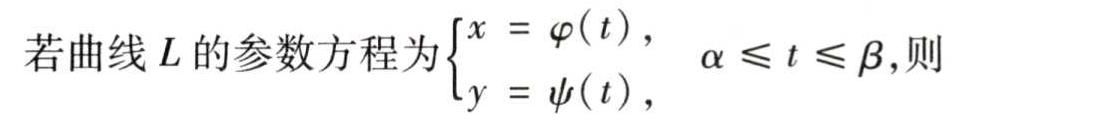
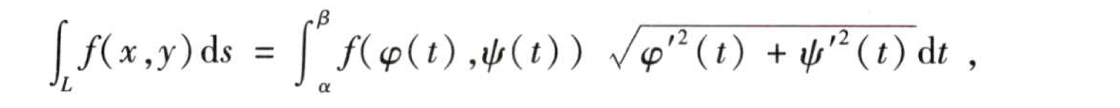
若是函数可以用y=y(x)表示,且x的表示范围为[a,b],则上式可以转换成:
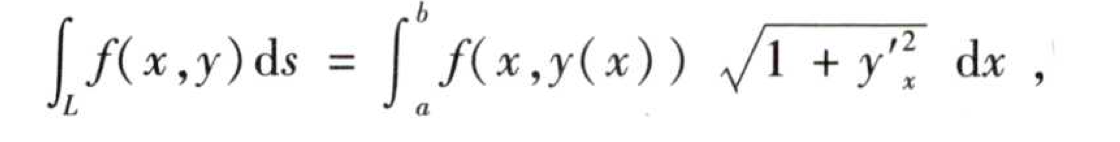
若是函数用极坐标r=r(θ)(θ范围为[a,b])表示,则可以表示为:
![]()
(2)对应地,第二类曲线积分为:

2.1.2 曲面积分化为二重积分
曲面积分转换的关键在于投影。
(1)第一类曲面积分

其中关于9.13中对于根号下方内容的推导过程如下:

(2)第二类曲面积分

此公式中的偏微分的来源是:

基于法向量的求法,可以求得9.15中偏微分的式子。从本质上来看,对于第二类曲面积分的计算的过程大致为:第二类????第一类????重积分,由此将计算过程转为便于计算的方式。
2.1.3 二重积分化为累次积分
二重化为累次的重要核心在于确定函数的积分域,确定这样的区域的核心在于画出示意图(对于几何图形需要有基本的认识)。转化为累次积分的方法有两种:先x后y和先y后x。如下图所示,前者适合先x后y,后者适合先y后x。
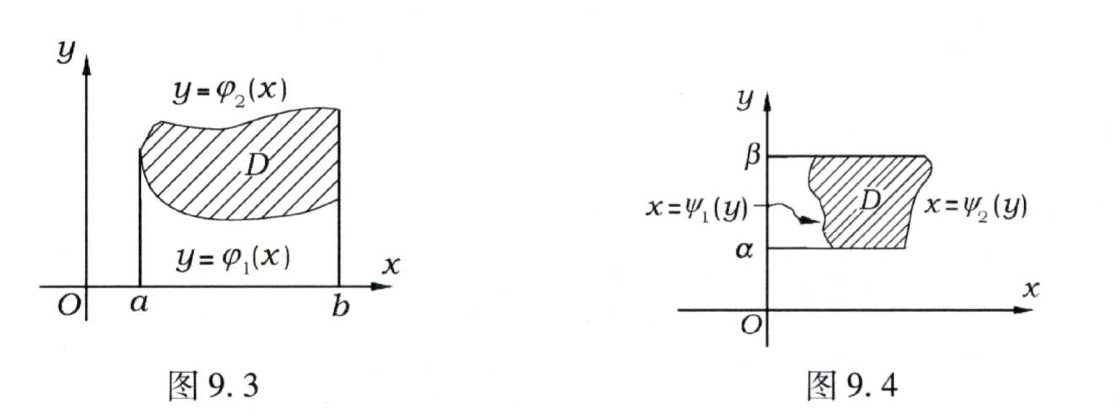
在确定过程中的一个技巧是分别作平行于x轴和y轴的直线,看这两条直线分别穿过区域后和区域边界的交点数量。若哪个方向上交点数量为2,则先积分哪个方向。
当积分区域为矩形时,属于特殊情况,这种情况下有如下特殊性质:
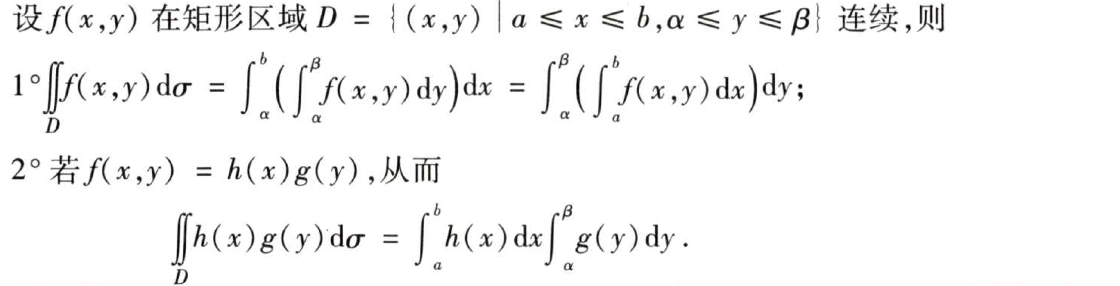
2.1.4三重积分化为累次积分
三重积分化为累次积分的情形也是分两种:先一后二和先二后一。
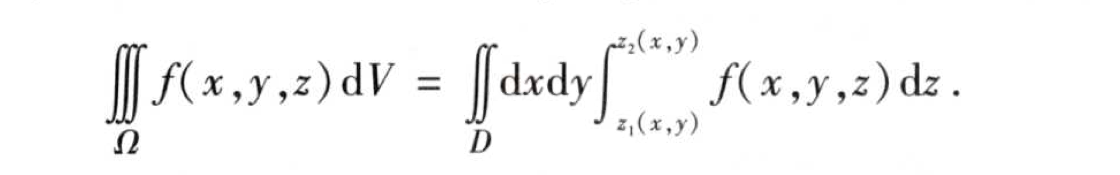
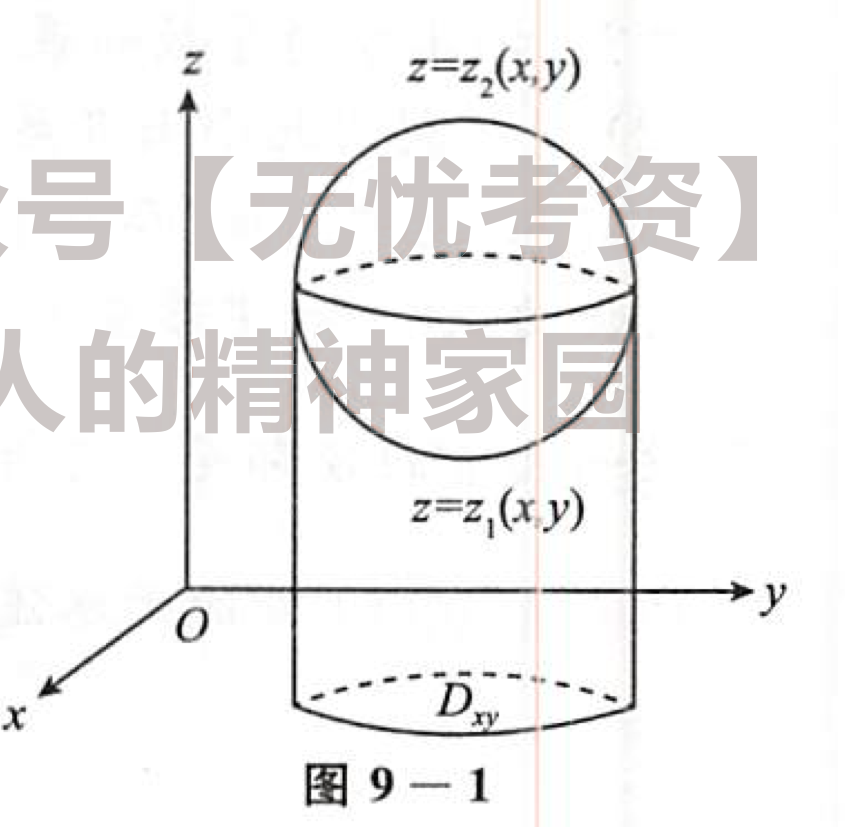
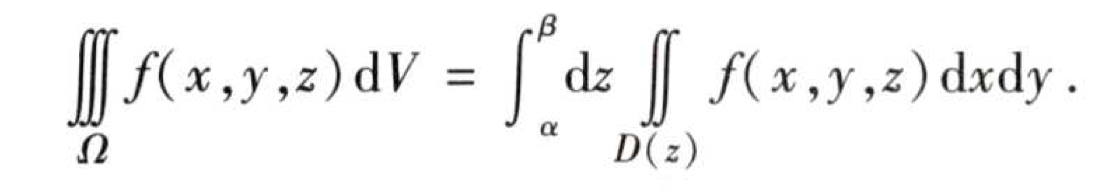
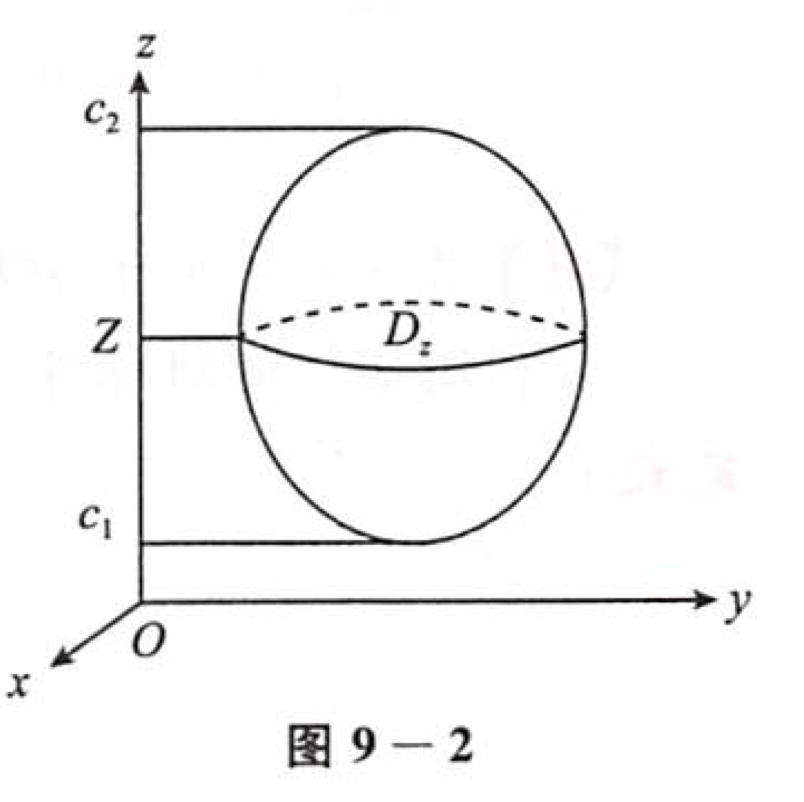
判断的方法也是很简单:若是截面易求,则先二后一(先求一次二重积分再求定积分),否则先一后二(先求定积分再求二重积分)。
2.2 按照几何意义计算
2.2.1 积分区域的平移
平移过程中保证面积/体积和形状不变,目的在于平移之后可以利用对称性和奇偶性。
(1)二元平面情形
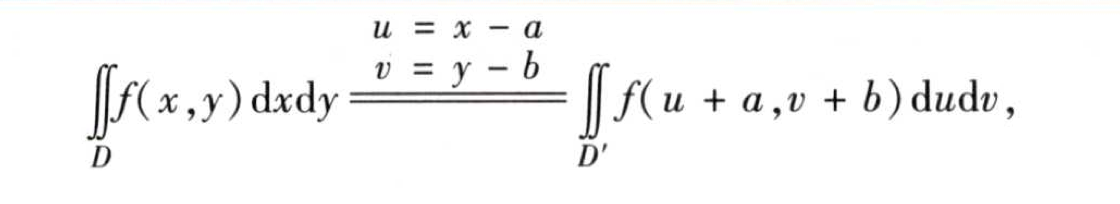
(2)三元空间情形
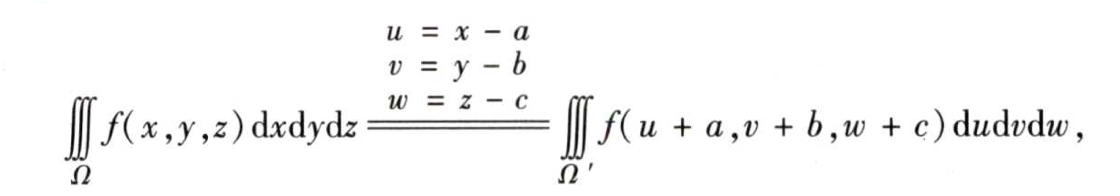
2.2.2 积分坐标的变换
2.2.2.1 二重积分的极坐标变换
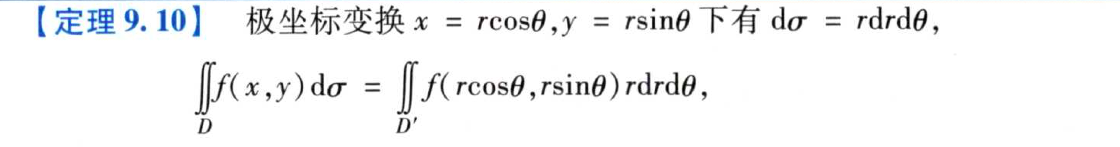
变换的过程的难点不在于将xy换成θ的形式,而在于确定二重积分各自的上下限。正元将上下限的确定分成了四种情形,大致如下:
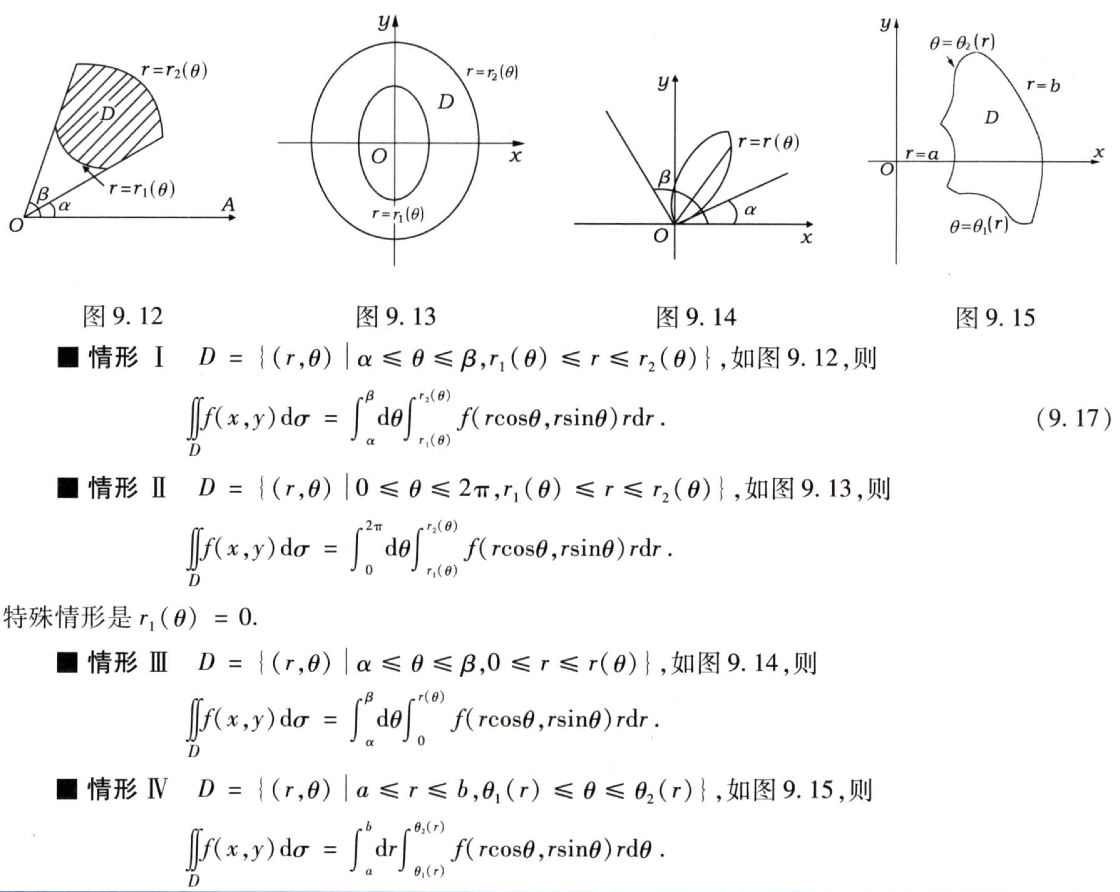
确定r的上下限范围的关键在于做一条从原点射出的射线,看这条射线和区域边界的交点是从哪里到哪里,由此推测出这样的上下限是多少。r的范围时从近到远,θ的范围是绕着逆时针从小到大。
2.2.2.2 三重积分的柱坐标变换
柱坐标是什么?看完下图同济教材的解析,应该可以有一定的了解。在这个坐标中,z坐标上为线性变换的量,而x轴和y轴则是在平面上进行变换。
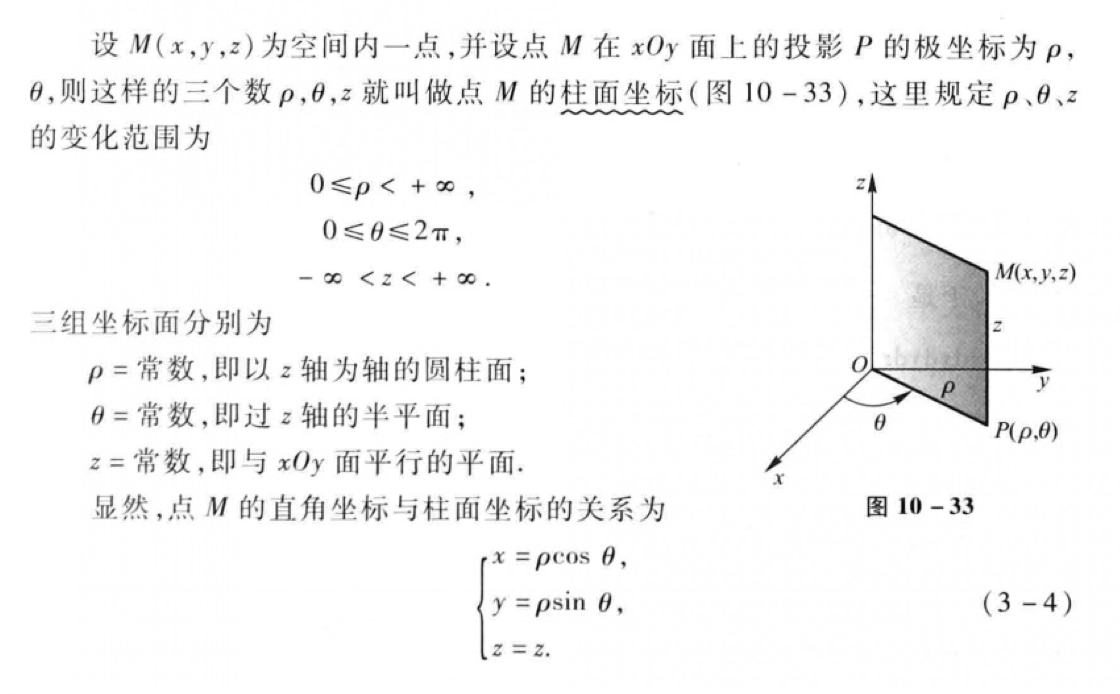
具体地变换中,将x和y分别进行参数的替换,计算公式如下:
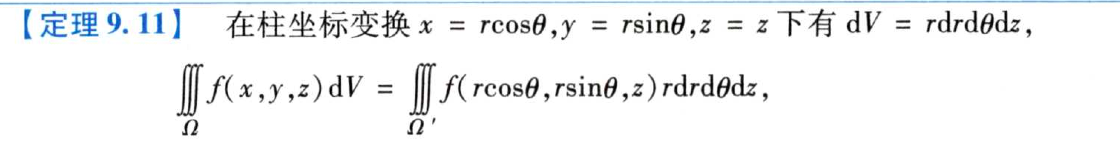
确定完上下限之后积分式可以表达为:
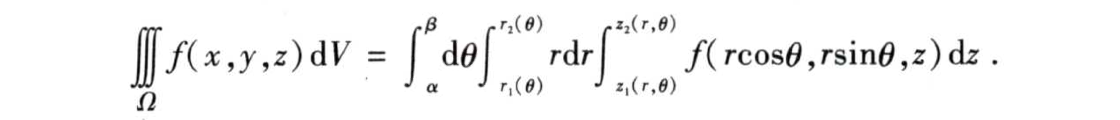
2.2.2.3 三重积分的球坐标变换
球坐标和柱坐标不同的是,球坐标将z轴方向上的变量也进行了参数的变换。
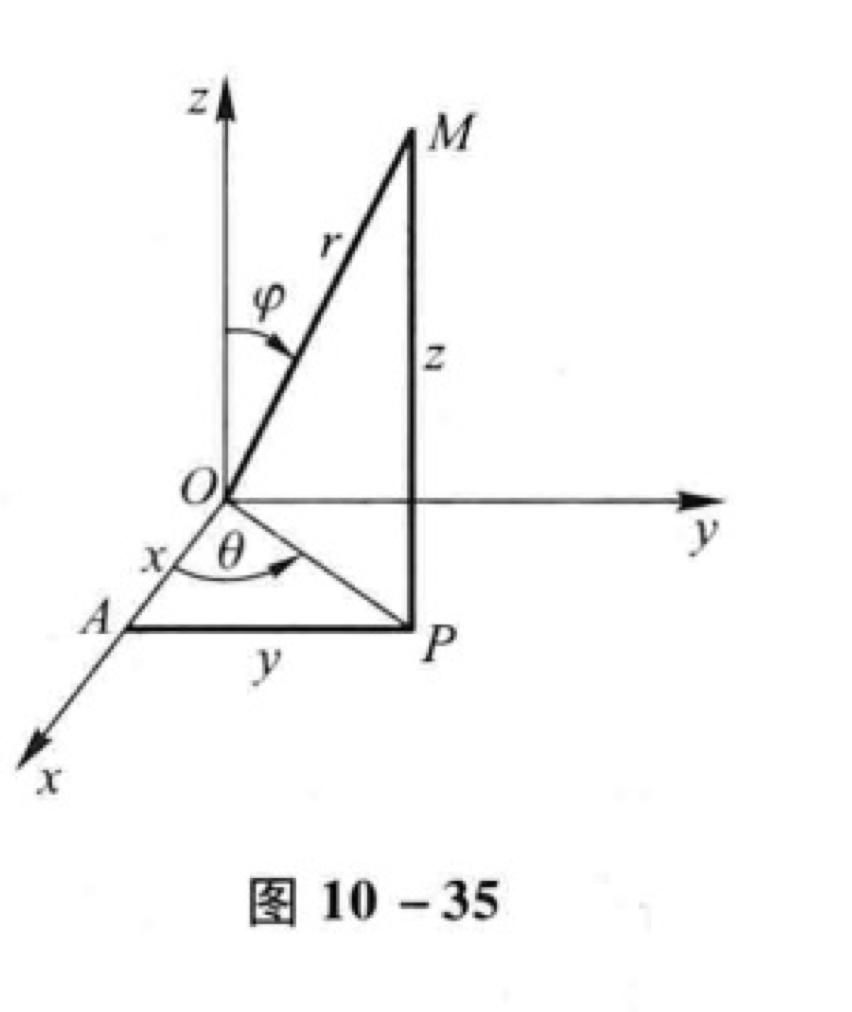
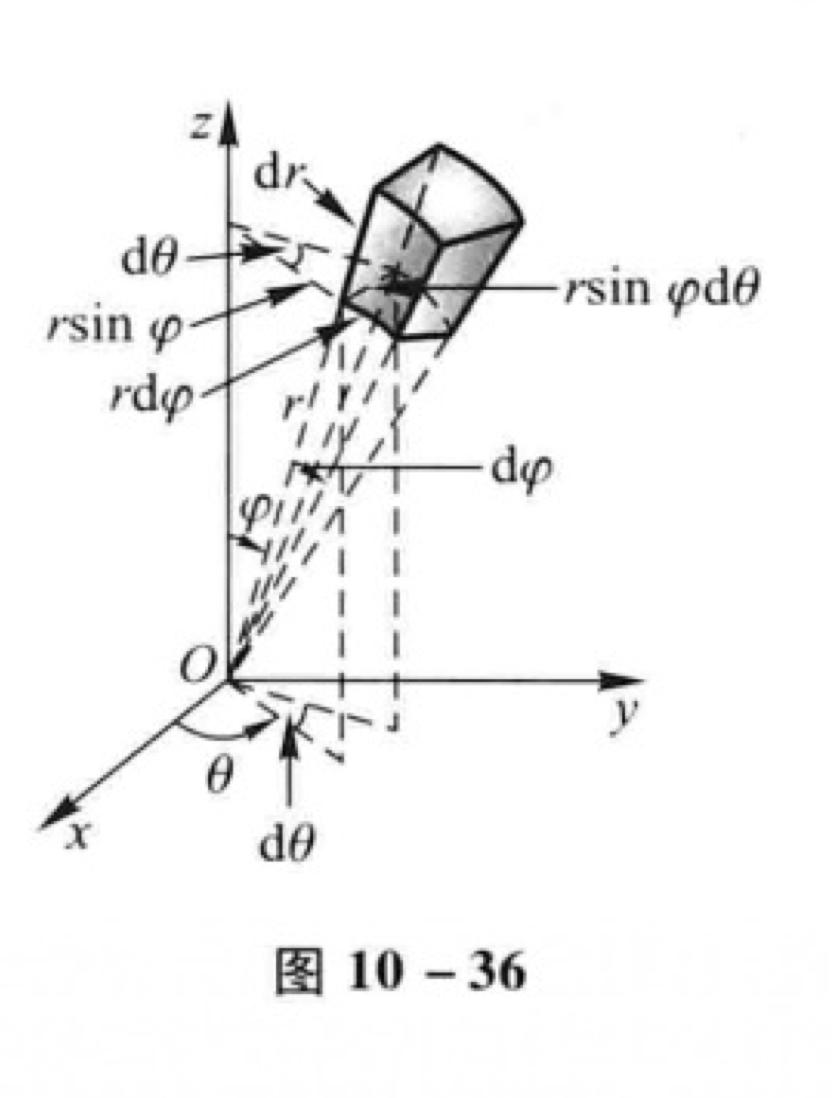

一般情形下的具体的公式为:
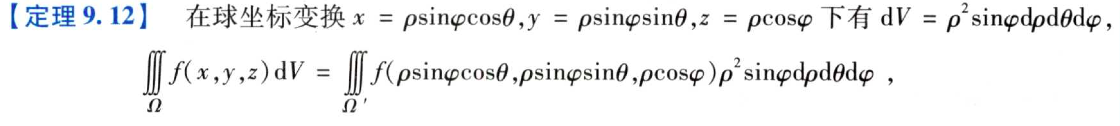
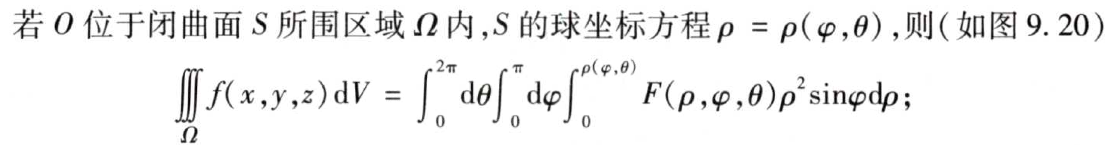
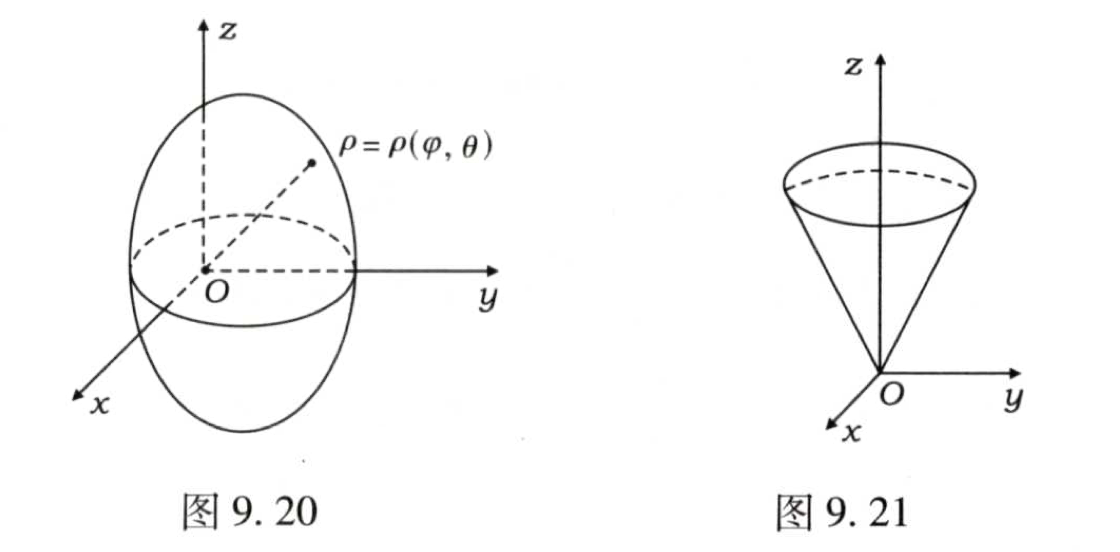
圆锥形状的区域则是球坐标情形下的一个特例,将φ的上限改为一个小于180度的角度值,则可以计算圆锥区域的三重积分,具体公式如下:
![]()
小小的总结:
三种坐标的积分顺序的变换的选择大致可以依照下表。
基本的原则是,若是属于xy可以相消或者平方和加根号的二元积分的情形,则可以将函数转换为极坐标进行计算。若是属于三重积分的情形,在z轴的值恒定的情形下,可以选择柱坐标进行替换。若不是,则可以选择球坐标进行替换。适当的对称性奇偶性的利用可以使得整体运算简便。

2.2.3 更换积分顺序
更换积分顺序的步骤清晰明了,大致可以划分为一下几个步骤:
1、根据累次积分确定此时的上下限的范围
2、画出此区域范围
3、用与第一步中不一样的顺序来确定积分上下限的值
2.2.4 利用对称性奇偶性
2.2.4.1 二重积分情形
基本原则是,积分区域关于某轴对称,则若此函数是对于另一个参数的奇函数,积分值为0,否则为2倍的积分,具体信息如下:

2.2.4.2 三重积分的情形
若积分区域关于某平面对称,则函数为第三个字母的奇函数时,积分为0,否则为积分的2倍,具体如下:

2.2.4.3 一类曲线面
若函数的积分曲线/面关于某坐标轴或者某平面对称,则函数在关于另一个参数的坐标轴/平面时奇函数的时候积分为0,否则积分为2倍。

2.2.4.4 二类曲线面
一步中不一样的顺序来确定积分上下限的值
2.2.5 分块积分
分块积分的主要应用情形为:
1、区域边界分段
2、被积函数分段
2.2.6 利用几何和物理意义计算
武忠祥的讲解中多使用质心作为计算过程中简化的依据,正元的书中也有类似的习题,例题如下:
![]()
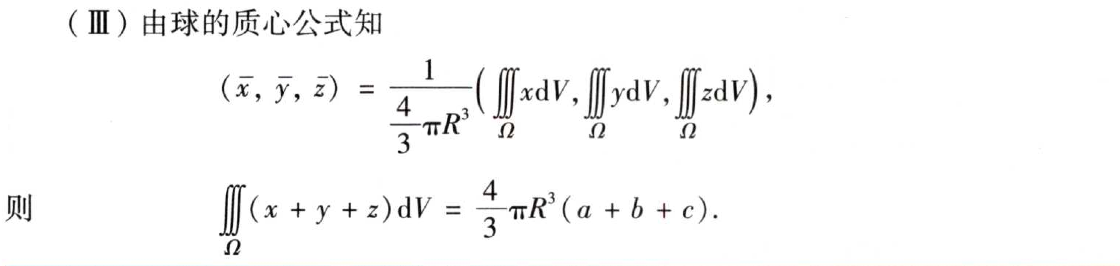
2.3 按照特殊公式计算
2.3.1 三大物理量:旋度、散度、通量
此部分武忠祥总结得更简单,具体如下

但是正元的书中以更加严谨的方法总结出这三个值的关系。
(1)通量&散度——高斯公式
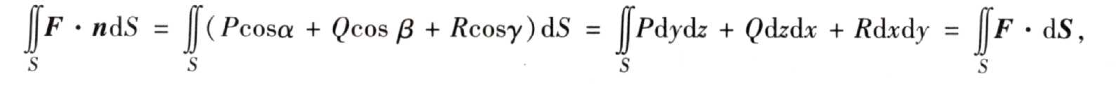

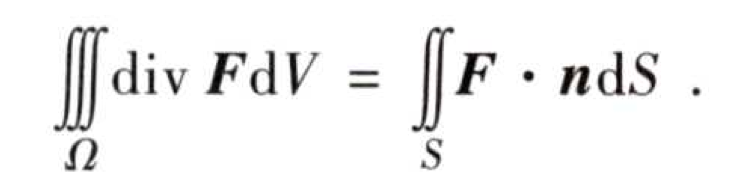
(2)环流量&旋度——斯托克斯公式
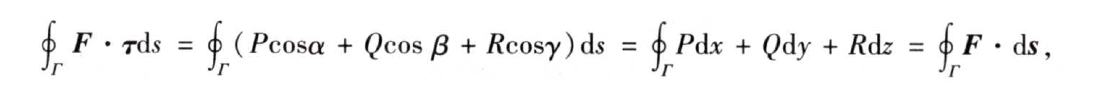
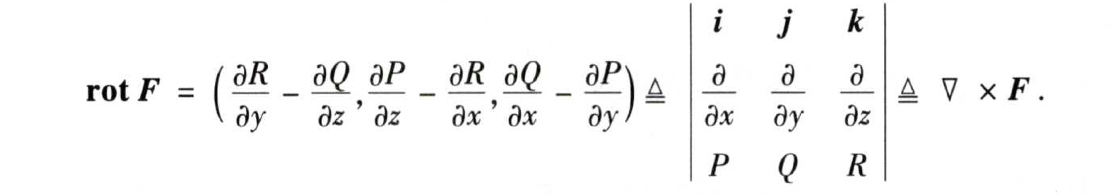
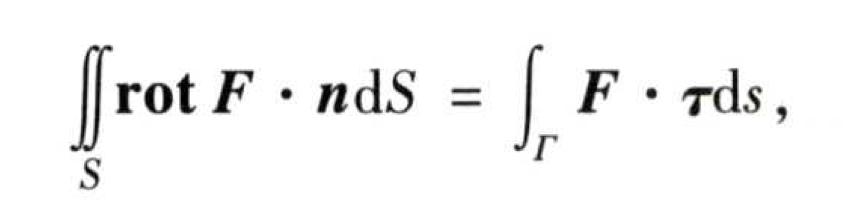
2.3.2 三大积分计算公式
在谈及三大特殊公式之前,教材上说到了一个概念叫连通区域,在说到连通区域的时候,不可调避的是关于连通区域的方向如何判定。
连通区域对立的是负连通区域。负连通区域是指一块区域内存在着若干的“洞”,而连通区域则是不存在洞的区域。关于负连通区域的方向,判定方法是假定区域在自己的左手边,绕着区域逆时针走一圈,如此为正,否则为负。
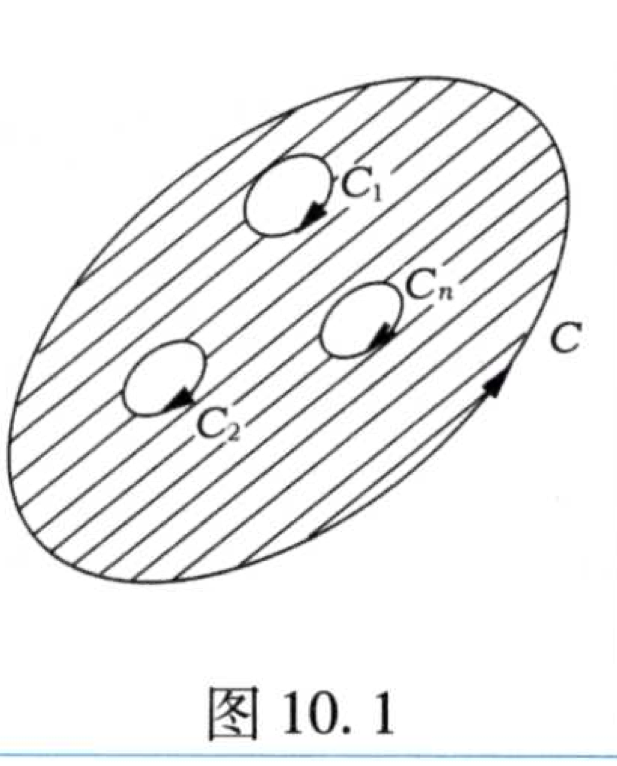
如上图所示,区域的正负一目了然,但是要注意区域外和区域内的洞的正向相反。
2.3.2.1 格林公式
第二类曲线积分转换为二重积分

2.3.2.2 高斯公式公式
曲面积分转换为三重积分
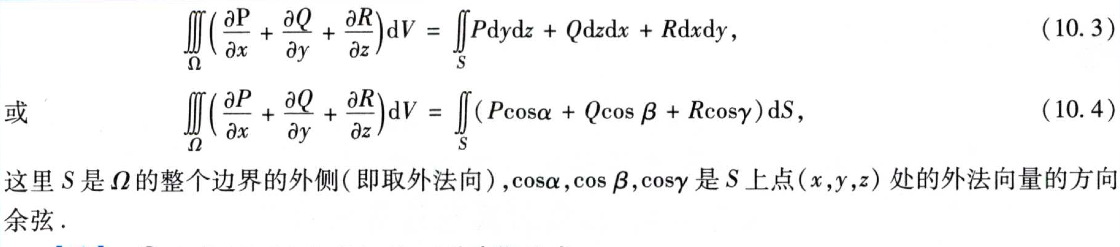
2.3.2.3 斯托克斯公式
简化曲线积分的计算,建立空间曲线和曲面的关系
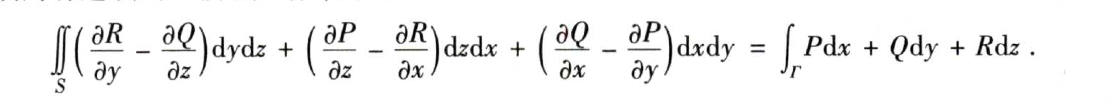
2.3.3 与积分路径无关
2.3.3.1 是什么

2.3.3.2 有何特征

2.3.3.3 如何判定


注意,方法三一般用以构造使用三大公式的条件。
2.3.3.4 如何用
关键在于构造出闭合的曲线/曲面空间,利用简单的特殊路径求取积分的值。



3、应用
3.1 几何应用
3.1.1 几何体积的计算
3.1.2 曲面面积的计算
3.2 物理应用
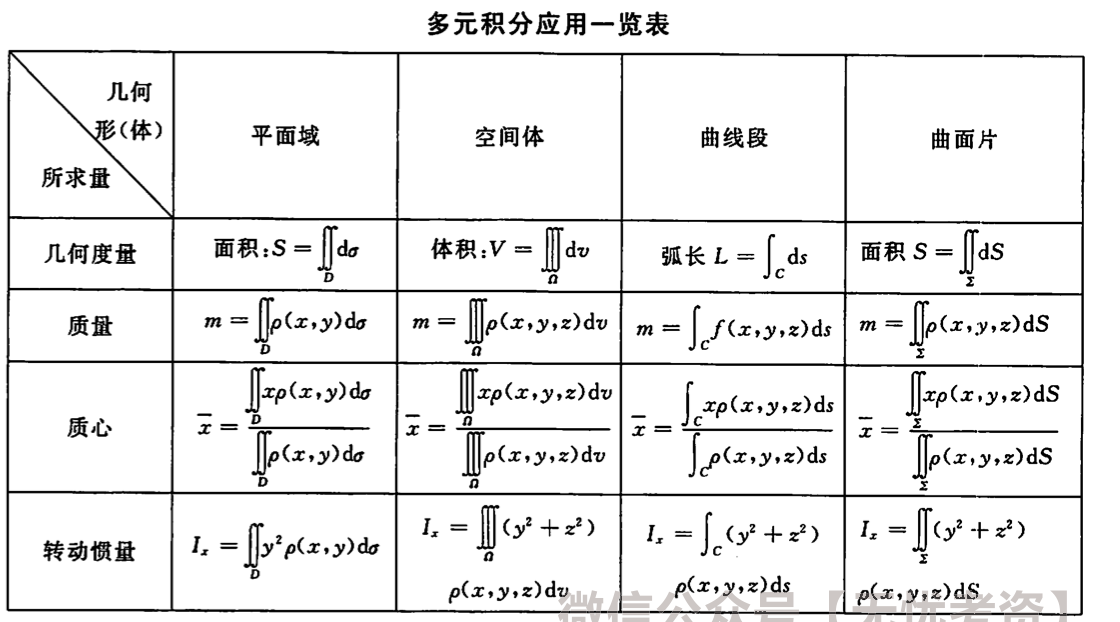
3.2.1 计算形心、质心、转动惯量
这一部分总体而言武忠祥总结得更好,大致如下表所示:
3.2.2 计算引力

3.2.3 计算功

3.2.3 计算流量
最后
以上就是纯真寒风最近收集整理的关于正元-多元积分笔记多元积分的全部内容,更多相关正元-多元积分笔记多元积分内容请搜索靠谱客的其他文章。








发表评论 取消回复