高等数学(第七版)同济大学 习题10-2(前10题)
函数作图软件:Mathematica
1. 计 算 下 列 二 重 积 分 : begin{aligned}&1. 计算下列二重积分:&end{aligned} 1. 计算下列二重积分:
( 1 ) ∬ D ( x 2 + y 2 ) d σ , 其 中 D = { ( x , y ) ∣ ∣ x ∣ ≤ 1 , ∣ y ∣ ≤ 1 } ; ( 2 ) ∬ D ( 3 x + 2 y ) d σ , 其 中 D 是 由 两 坐 标 轴 及 直 线 x + y = 2 所 围 成 的 闭 区 域 ; ( 3 ) ∬ D ( x 3 + 3 x 2 y + y 3 ) d σ , 其 中 D = { ( x , y ) ∣ 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 } ; ( 4 ) ∬ D x c o s ( x + y ) d σ , 其 中 D 是 顶 点 分 别 为 ( 0 , 0 ) , ( π , 0 ) 和 ( π , π ) 的 三 角 形 闭 区 域 . begin{aligned} & (1) iint_D (x^2+y^2)dsigma,其中D={(x, y) | |x| le 1,|y| le 1};\\ & (2) iint_D (3x+2y)dsigma,其中D是由两坐标轴及直线x+y=2所围成的闭区域;\\ & (3) iint_D (x^3+3x^2y+y^3)dsigma,其中D={(x, y) | 0 le x le 1,0 le y le 1};\\ & (4) iint_D xcos(x+y)dsigma,其中D是顶点分别为(0, 0),(pi, 0)和(pi, pi)的三角形闭区域. & end{aligned} (1) ∬D(x2+y2)dσ,其中D={(x, y) ∣ ∣x∣≤1,∣y∣≤1}; (2) ∬D(3x+2y)dσ,其中D是由两坐标轴及直线x+y=2所围成的闭区域; (3) ∬D(x3+3x2y+y3)dσ,其中D={(x, y) ∣ 0≤x≤1,0≤y≤1}; (4) ∬Dxcos(x+y)dσ,其中D是顶点分别为(0, 0),(π, 0)和(π, π)的三角形闭区域.
解:
( 1 ) ∬ D ( x 2 + y 2 ) d σ = ∫ − 1 1 d x ∫ − 1 1 ( x 2 + y 2 ) d y = ∫ − 1 1 [ x 2 y + y 3 3 ] − 1 1 d x = ∫ − 1 1 ( 2 x 2 + 2 3 ) d x = 8 3 . ( 2 ) D 可 用 不 等 式 表 示 为 0 ≤ y ≤ 2 − x , 0 ≤ x ≤ 2 , 则 ∬ D ( 3 x + 2 y ) d σ = ∫ 0 2 d x ∫ 0 2 − x ( 3 x + 2 y ) d y = ∫ 0 2 [ 3 x y + y 2 ] 0 2 − x d x = ∫ 0 2 ( 4 + 2 x − 2 x 2 ) d x = 20 3 . ( 3 ) ∬ D ( x 3 + 3 x 2 y + y 3 ) d σ = ∫ 0 1 d y ∫ 0 1 ( x 3 + 3 x 2 y + y 3 ) d x = ∫ 0 1 [ x 4 4 + x 3 y + y 3 x ] 0 1 d y = ∫ 0 1 ( 1 4 + y + y 3 ) d y = 1. ( 4 ) D 可 用 不 等 式 表 示 为 0 ≤ y ≤ x , 0 ≤ x ≤ π , 则 ∬ D x c o s ( x + y ) d σ = ∫ 0 π x d x ∫ 0 x c o s ( x + y ) d y = ∫ 0 π x [ s i n ( x + y ) ] 0 x d x = ∫ 0 π x ( s i n 2 x − s i n x ) d x = ∫ 0 π x d ( c o s x − 1 2 c o s 2 x ) ) = [ x ( c o s x − 1 2 c o s 2 x ) ] 0 π − ∫ 0 π ( c o s x − 1 2 c o s 2 x ) d x = π ( − 1 − 1 2 ) − 0 = − 3 2 π . begin{aligned} & (1) iint_D (x^2+y^2)dsigma=int_{-1}^{1}dxint_{-1}^{1}(x^2+y^2)dy=int_{-1}^{1}left[x^2y+frac{y^3}{3}right]_{-1}^{1}dx=int_{-1}^{1}left(2x^2+frac{2}{3}right)dx=frac{8}{3}.\\ & (2) D可用不等式表示为0 le y le 2-x,0 le x le 2,则iint_D (3x+2y)dsigma=\\ & int_{0}^{2}dxint_{0}^{2-x}(3x+2y)dy=int_{0}^{2}[3xy+y^2]_{0}^{2-x}dx=int_{0}^{2}(4+2x-2x^2)dx=frac{20}{3}.\\ & (3) iint_D (x^3+3x^2y+y^3)dsigma=int_{0}^{1}dyint_{0}^{1}(x^3+3x^2y+y^3)dx=int_{0}^{1}left[frac{x^4}{4}+x^3y+y^3xright]_{0}^{1}dy=int_{0}^{1}left(frac{1}{4}+y+y^3right)dy=1.\\ & (4) D可用不等式表示为0 le y le x,0 le x le pi,则iint_D xcos(x+y)dsigma=int_{0}^{pi}xdxint_{0}^{x}cos(x+y)dy=\\ & int_{0}^{pi}x[sin(x+y)]_{0}^{x}dx=int_{0}^{pi}x(sin 2x-sin x)dx=int_{0}^{pi}xdleft(cos x-frac{1}{2}cos 2x)right)=\\ & left[xleft(cos x-frac{1}{2}cos 2xright)right]_{0}^{pi}-int_{0}^{pi}left(cos x-frac{1}{2}cos 2xright)dx=pileft(-1-frac{1}{2}right)-0=-frac{3}{2}pi. & end{aligned} (1) ∬D(x2+y2)dσ=∫−11dx∫−11(x2+y2)dy=∫−11[x2y+3y3]−11dx=∫−11(2x2+32)dx=38. (2) D可用不等式表示为0≤y≤2−x,0≤x≤2,则∬D(3x+2y)dσ= ∫02dx∫02−x(3x+2y)dy=∫02[3xy+y2]02−xdx=∫02(4+2x−2x2)dx=320. (3) ∬D(x3+3x2y+y3)dσ=∫01dy∫01(x3+3x2y+y3)dx=∫01[4x4+x3y+y3x]01dy=∫01(41+y+y3)dy=1. (4) D可用不等式表示为0≤y≤x,0≤x≤π,则∬Dxcos(x+y)dσ=∫0πxdx∫0xcos(x+y)dy= ∫0πx[sin(x+y)]0xdx=∫0πx(sin 2x−sin x)dx=∫0πxd(cos x−21cos 2x))= [x(cos x−21cos 2x)]0π−∫0π(cos x−21cos 2x)dx=π(−1−21)−0=−23π.
2. 画 出 积 分 区 域 , 并 计 算 下 列 二 重 积 分 : begin{aligned}&2. 画出积分区域,并计算下列二重积分:&end{aligned} 2. 画出积分区域,并计算下列二重积分:
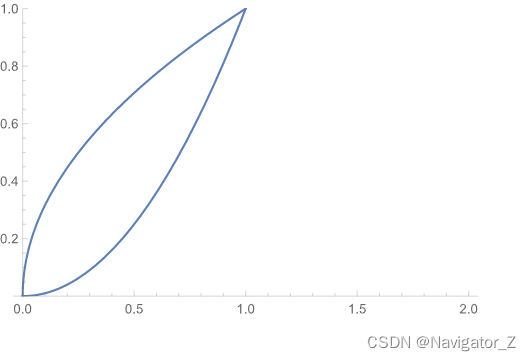
( 1 ) ∬ D x y d σ , 其 中 D 是 由 两 条 抛 物 线 y = x , y = x 2 所 围 成 的 闭 区 域 ; ( 2 ) ∬ D x y 2 d σ , 其 中 D 是 由 圆 周 x 2 + y 2 = 4 及 y 轴 所 围 成 的 右 半 闭 区 域 ; ( 3 ) ∬ D e x + y d σ , 其 中 D = { ( x , y ) ∣ ∣ x ∣ + ∣ y ∣ ≤ 1 } ; ( 4 ) ∬ D ( x 2 + y 2 − x ) d σ , 其 中 D 是 由 直 线 y = 2 , y = x 及 y = 2 x 所 围 成 的 闭 区 域 . begin{aligned} & (1) iint_D xsqrt{y}dsigma,其中D是由两条抛物线y=sqrt{x},y=x^2所围成的闭区域;\\ & (2) iint_D xy^2dsigma,其中D是由圆周x^2+y^2=4及y轴所围成的右半闭区域;\\ & (3) iint_D e^{x+y}dsigma,其中D={(x, y) | |x|+|y| le 1};\\ & (4) iint_D (x^2+y^2-x)dsigma,其中D是由直线y=2,y=x及y=2x所围成的闭区域. & end{aligned} (1) ∬Dxydσ,其中D是由两条抛物线y=x,y=x2所围成的闭区域; (2) ∬Dxy2dσ,其中D是由圆周x2+y2=4及y轴所围成的右半闭区域; (3) ∬Dex+ydσ,其中D={(x, y) ∣ ∣x∣+∣y∣≤1}; (4) ∬D(x2+y2−x)dσ,其中D是由直线y=2,y=x及y=2x所围成的闭区域.
解:
(
1
)
D
用
不
等
式
表
示
为
x
2
≤
y
≤
x
,
0
≤
x
≤
1
,
则
∬
D
x
y
d
σ
=
∫
0
1
x
d
x
∫
x
2
x
y
d
y
=
2
3
∫
0
1
x
[
y
3
2
]
x
2
x
d
x
=
2
3
∫
0
1
(
x
7
4
−
x
4
)
d
x
=
6
55
.
begin{aligned} & (1) D用不等式表示为x^2 le y le sqrt{x},0 le x le 1,则\\ & iint_D xsqrt{y}dsigma=int_{0}^{1}xdxint_{x^2}^{sqrt{x}}sqrt{y}dy=frac{2}{3}int_{0}^{1}xleft[y^{frac{3}{2}}right]_{x^2}^{sqrt{x}}dx=frac{2}{3}int_{0}^{1}(x^{frac{7}{4}}-x^4)dx=frac{6}{55}.\\ & end{aligned}
(1) D用不等式表示为x2≤y≤x,0≤x≤1,则 ∬Dxydσ=∫01xdx∫x2xydy=32∫01x[y23]x2xdx=32∫01(x47−x4)dx=556.
(
2
)
D
用
不
等
式
表
示
为
0
≤
x
≤
4
−
y
2
,
−
2
≤
y
≤
2
,
则
∬
D
x
y
2
d
σ
=
∫
−
2
2
y
2
d
y
∫
0
4
−
y
2
x
d
x
=
1
2
∫
−
2
2
y
2
(
4
−
y
2
)
d
y
=
64
15
.
begin{aligned} & (2) D用不等式表示为0 le x le sqrt{4-y^2},-2 le y le 2,则\\ & iint_D xy^2dsigma=int_{-2}^{2}y^2dyint_{0}^{sqrt{4-y^2}}xdx=frac{1}{2}int_{-2}^{2}y^2(4-y^2)dy=frac{64}{15}.\\ & end{aligned}
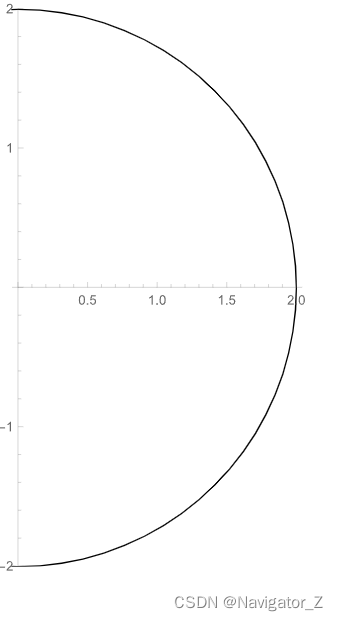
(2) D用不等式表示为0≤x≤4−y2,−2≤y≤2,则 ∬Dxy2dσ=∫−22y2dy∫04−y2xdx=21∫−22y2(4−y2)dy=1564.
(
3
)
D
=
D
1
∪
D
2
,
其
中
D
1
=
{
(
x
,
y
)
∣
−
x
−
1
≤
y
≤
x
+
1
,
−
1
≤
x
≤
0
}
,
D
2
=
{
(
x
,
y
)
∣
x
−
1
≤
y
≤
−
x
+
1
,
0
≤
x
≤
1
}
,
则
∬
D
e
x
+
y
d
σ
=
∬
D
1
e
x
+
y
d
σ
+
∬
D
2
e
x
+
y
d
σ
=
∫
−
1
0
e
x
d
x
∫
−
x
−
1
x
+
1
e
y
d
y
+
∫
0
1
e
x
d
x
∫
x
−
1
−
x
+
1
e
y
d
y
=
∫
−
1
0
(
e
2
x
+
1
−
e
−
1
)
d
x
+
∫
0
1
(
e
−
e
2
x
−
1
)
d
x
=
e
−
e
−
1
.
begin{aligned} & (3) D=D_1 cup D_2,其中D_1={(x, y) | -x-1 le y le x+1,-1 le x le 0},\\ & D_2={(x, y) | x-1 le y le -x+1,0 le x le 1},则\\ & iint_De^{x+y}dsigma=iint_{D_1}e^{x+y}dsigma+iint_{D_2}e^{x+y}dsigma=int_{-1}^{0}e^xdxint_{-x-1}^{x+1}e^ydy+int_{0}^{1}e^xdxint_{x-1}^{-x+1}e^ydy=\\ & int_{-1}^{0}(e^{2x+1}-e^{-1})dx+int_{0}^{1}(e-e^{2x-1})dx=e-e^{-1}.\\ & end{aligned}
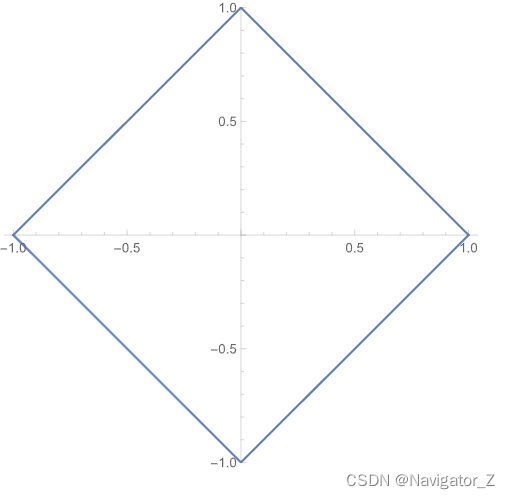
(3) D=D1∪D2,其中D1={(x, y) ∣ −x−1≤y≤x+1,−1≤x≤0}, D2={(x, y) ∣ x−1≤y≤−x+1,0≤x≤1},则 ∬Dex+ydσ=∬D1ex+ydσ+∬D2ex+ydσ=∫−10exdx∫−x−1x+1eydy+∫01exdx∫x−1−x+1eydy= ∫−10(e2x+1−e−1)dx+∫01(e−e2x−1)dx=e−e−1.
(
4
)
D
用
不
等
式
表
示
为
y
2
≤
x
≤
y
,
0
≤
y
≤
2
,
则
∬
D
(
x
2
+
y
2
−
x
)
d
σ
=
∫
0
2
d
y
∫
y
2
y
(
x
2
+
y
2
−
x
)
d
x
=
∫
0
2
[
1
3
x
3
+
x
y
2
−
1
2
x
2
]
y
2
y
d
y
=
∫
0
2
(
19
24
y
3
−
3
8
y
2
)
d
y
=
13
6
.
begin{aligned} & (4) D用不等式表示为frac{y}{2} le x le y,0 le y le 2,则\\ & iint_D (x^2+y^2-x)dsigma=int_{0}^{2}dyint_{frac{y}{2}}^{y}(x^2+y^2-x)dx=int_{0}^{2}left[frac{1}{3}x^3+xy^2-frac{1}{2}x^2right]_{frac{y}{2}}^{y}dy=int_{0}^{2}left(frac{19}{24}y^3-frac{3}{8}y^2right)dy=frac{13}{6}. & end{aligned}
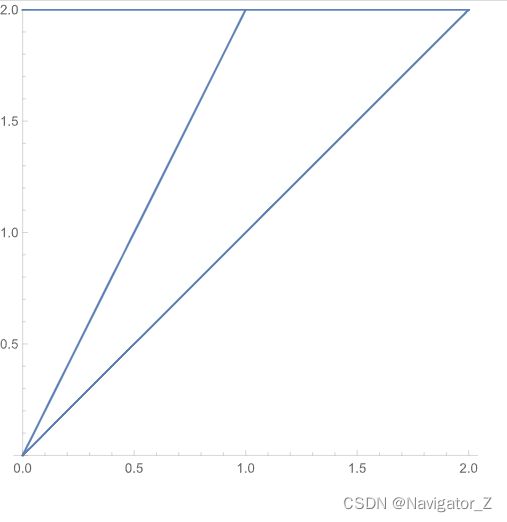
(4) D用不等式表示为2y≤x≤y,0≤y≤2,则 ∬D(x2+y2−x)dσ=∫02dy∫2yy(x2+y2−x)dx=∫02[31x3+xy2−21x2]2yydy=∫02(2419y3−83y2)dy=613.
3. 如 果 二 重 积 分 ∬ D f ( x , y ) d x d y 的 被 积 函 数 f ( x , y ) 是 两 个 函 数 f 1 ( x ) 及 f 2 ( y ) 的 乘 积 , 即 f ( x , y ) = f 1 ( x ) ⋅ f 2 ( y ) , 积 分 区 域 D = { ( x , y ) ∣ a ≤ x ≤ b , c ≤ y ≤ d } , 证 明 这 个 二 重 积 分 等 于 两 个 单 积 分 的 乘 积 , 即 ∬ D f 1 ( x ) ⋅ f 2 ( y ) d x d y = [ ∫ a b f 1 ( x ) d x ] ⋅ [ ∫ c d f 2 ( y ) d y ] . begin{aligned}&3. 如果二重积分iint_{D}f(x, y)dxdy的被积函数f(x, y)是两个函数f_1(x)及f_2(y)的乘积,即\\& f(x, y)=f_1(x)cdot f_2(y),积分区域D={(x, y) | ale x le b,c le y le d},证明这个二重积分\\& 等于两个单积分的乘积,即iint_{D}f_1(x)cdot f_2(y)dxdy=left[int_{a}^{b}f_1(x)dxright]cdotleft[int_{c}^{d}f_2(y)dyright].&end{aligned} 3. 如果二重积分∬Df(x, y)dxdy的被积函数f(x, y)是两个函数f1(x)及f2(y)的乘积,即 f(x, y)=f1(x)⋅f2(y),积分区域D={(x, y) ∣ a≤x≤b,c≤y≤d},证明这个二重积分 等于两个单积分的乘积,即∬Df1(x)⋅f2(y)dxdy=[∫abf1(x)dx]⋅[∫cdf2(y)dy].
解:
∬ D f 1 ( x ) ⋅ f 2 ( y ) d x d y = ∫ a b [ ∫ c d f 1 ( x ) ⋅ f 2 ( y ) d y ] d x , 上 式 右 端 第 一 次 单 积 分 ∫ c d f 1 ( x ) ⋅ f 2 ( y ) 中 , f 1 ( x ) 与 积 分 变 量 y 无 关 , 可 作 为 常 数 提 到 积 分 外 , 因 此 变 为 ∫ a b f 1 ( x ) ⋅ [ ∫ c d f 2 ( y ) d y ] d x , 在 该 积 分 中 , 因 为 ∫ c d f 2 ( y ) d y 为 常 数 , 所 以 也 可 提 到 积 分 外 , 得 ∬ D f 1 ( x ) ⋅ f 2 ( y ) d x d y = [ ∫ c d f 2 ( y ) d y ] ⋅ [ ∫ a b f 1 ( x ) d x ] = [ ∫ a b f 1 ( x ) d x ] ⋅ [ ∫ c d f 2 ( y ) d y ] begin{aligned} & iint_{D}f_1(x)cdot f_2(y)dxdy=int_{a}^{b}left[int_{c}^{d}f_1(x)cdot f_2(y)dyright]dx,上式右端第一次单积分int_{c}^{d}f_1(x)cdot f_2(y)中,f_1(x)与\\ & 积分变量y无关,可作为常数提到积分外,因此变为int_{a}^{b}f_1(x) cdot left[int_{c}^{d}f_2(y)dyright]dx,在该积分中,因为\\ & int_{c}^{d}f_2(y)dy为常数,所以也可提到积分外,得\\ & iint_{D}f_1(x)cdot f_2(y)dxdy=left[int_{c}^{d}f_2(y)dyright]cdot left[int_{a}^{b}f_1(x)dxright]=left[int_{a}^{b}f_1(x)dxright]cdotleft[int_{c}^{d}f_2(y)dyright] & end{aligned} ∬Df1(x)⋅f2(y)dxdy=∫ab[∫cdf1(x)⋅f2(y)dy]dx,上式右端第一次单积分∫cdf1(x)⋅f2(y)中,f1(x)与 积分变量y无关,可作为常数提到积分外,因此变为∫abf1(x)⋅[∫cdf2(y)dy]dx,在该积分中,因为 ∫cdf2(y)dy为常数,所以也可提到积分外,得 ∬Df1(x)⋅f2(y)dxdy=[∫cdf2(y)dy]⋅[∫abf1(x)dx]=[∫abf1(x)dx]⋅[∫cdf2(y)dy]
4. 化 二 重 积 分 I = ∬ D f ( x , y ) d σ 为 二 次 积 分 ( 分 别 列 出 对 两 个 变 量 先 后 次 序 不 同 的 两 个 二 次 积 分 ) , 其 中 积 分 区 域 D 是 : begin{aligned}&4. 化二重积分I=iint_{D}f(x, y)dsigma为二次积分(分别列出对两个变量先后次序不同的两个二次积分),\\& 其中积分区域D是:&end{aligned} 4. 化二重积分I=∬Df(x, y)dσ为二次积分(分别列出对两个变量先后次序不同的两个二次积分), 其中积分区域D是:
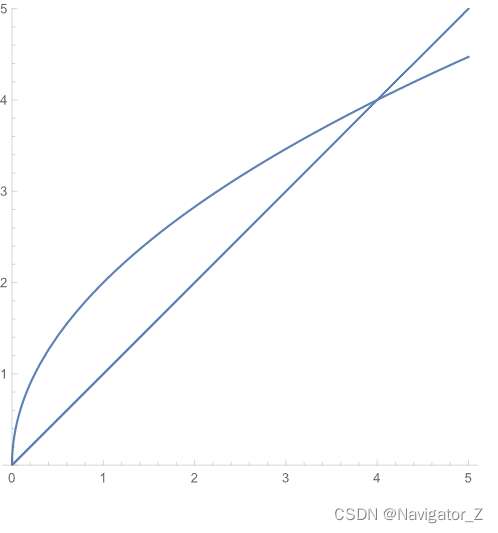
( 1 ) 由 直 线 y = x 及 抛 物 线 y 2 = 4 x 所 围 成 的 闭 区 域 ; ( 2 ) 由 x 轴 及 半 圆 周 x 2 + y 2 = r 2 ( y ≥ 0 ) 所 围 成 的 闭 区 域 ; ( 3 ) 由 直 线 y = x , x = 2 及 双 曲 线 y = 1 x ( x > 0 ) 所 围 成 的 闭 区 域 ; ( 4 ) 环 形 闭 区 域 { ( x , y ) ∣ 1 ≤ x 2 + y 2 ≤ 4 } . begin{aligned} & (1) 由直线y=x及抛物线y^2=4x所围成的闭区域;\\ & (2) 由x轴及半圆周x^2+y^2=r^2(y ge 0)所围成的闭区域;\\ & (3) 由直线y=x,x=2及双曲线y=frac{1}{x}(x gt 0)所围成的闭区域;\\ & (4) 环形闭区域{(x, y) | 1 le x^2+y^2 le 4}. & end{aligned} (1) 由直线y=x及抛物线y2=4x所围成的闭区域; (2) 由x轴及半圆周x2+y2=r2(y≥0)所围成的闭区域; (3) 由直线y=x,x=2及双曲线y=x1(x>0)所围成的闭区域; (4) 环形闭区域{(x, y) ∣ 1≤x2+y2≤4}.
解:
(
1
)
直
线
y
=
x
及
抛
物
线
y
2
=
4
x
的
交
点
为
(
0
,
0
)
和
(
4
,
4
)
,
则
I
=
∫
0
4
d
x
∫
x
4
x
f
(
x
,
y
)
d
y
,
或
I
=
∫
0
4
d
x
∫
y
2
4
y
f
(
x
,
y
)
d
y
.
begin{aligned} & (1) 直线y=x及抛物线y^2=4x的交点为(0, 0)和(4, 4),则I=int_{0}^{4}dxint_{x}^{sqrt{4x}}f(x, y)dy,或I=int_{0}^{4}dxint_{frac{y^2}{4}}^{y}f(x, y)dy.\\ & end{aligned}
(1) 直线y=x及抛物线y2=4x的交点为(0, 0)和(4, 4),则I=∫04dx∫x4xf(x, y)dy,或I=∫04dx∫4y2yf(x, y)dy.
(
2
)
D
用
不
等
式
表
示
为
0
≤
y
≤
r
2
−
x
2
,
−
r
≤
x
≤
r
,
则
将
I
化
为
先
对
y
后
对
x
的
二
次
积
分
,
I
=
∫
−
r
r
d
x
∫
0
r
2
−
x
2
f
(
x
,
y
)
d
y
,
D
用
不
等
式
表
示
为
−
r
2
−
y
2
≤
x
≤
r
2
−
y
2
,
0
≤
y
≤
r
,
则
将
I
化
为
先
对
x
后
对
y
的
二
次
积
分
,
I
=
∫
0
r
d
y
∫
−
r
2
−
y
2
r
2
−
y
2
f
(
x
,
y
)
d
x
.
(
3
)
三
条
曲
线
两
两
相
交
,
得
3
个
交
点
(
1
,
1
)
,
(
2
,
1
2
)
和
(
2
,
2
)
,
则
I
=
∫
1
2
d
x
∫
1
x
x
f
(
x
,
y
)
d
y
,
或
I
=
∫
1
2
1
d
y
∫
1
y
2
f
(
x
,
y
)
d
x
+
∫
1
2
d
y
∫
y
2
f
(
x
,
y
)
d
x
.
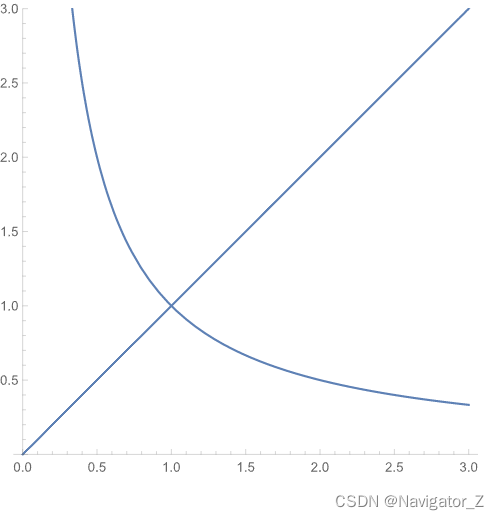
begin{aligned} & (2) D用不等式表示为0 le y le sqrt{r^2-x^2},-r le x le r,则将I化为先对y后对x的二次积分,\\ & I=int_{-r}^{r}dxint_{0}^{sqrt{r^2-x^2}}f(x, y)dy,\\ & D用不等式表示为-sqrt{r^2-y^2} le x le sqrt{r^2-y^2},0 le y le r,则将I化为先对x后对y的二次积分,\\ & I=int_{0}^{r}dyint_{-sqrt{r^2-y^2}}^{sqrt{r^2-y^2}}f(x, y)dx.\\ & (3) 三条曲线两两相交,得3个交点(1, 1),left(2, frac{1}{2}right)和(2, 2),则I=int_{1}^{2}dxint_{frac{1}{x}}^{x}f(x, y)dy,\\ & 或I=int_{frac{1}{2}}^{1}dyint_{frac{1}{y}}^{2}f(x, y)dx+int_{1}^{2}dyint_{y}^{2}f(x, y)dx.\\ & end{aligned}
(2) D用不等式表示为0≤y≤r2−x2,−r≤x≤r,则将I化为先对y后对x的二次积分, I=∫−rrdx∫0r2−x2f(x, y)dy, D用不等式表示为−r2−y2≤x≤r2−y2,0≤y≤r,则将I化为先对x后对y的二次积分, I=∫0rdy∫−r2−y2r2−y2f(x, y)dx. (3) 三条曲线两两相交,得3个交点(1, 1),(2, 21)和(2, 2),则I=∫12dx∫x1xf(x, y)dy, 或I=∫211dy∫y12f(x, y)dx+∫12dy∫y2f(x, y)dx.
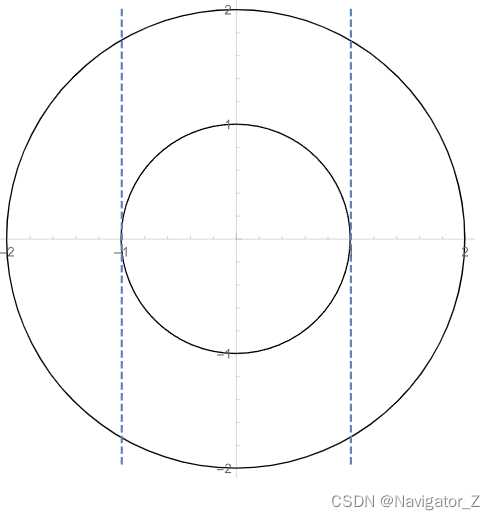
(
4
)
将
积
分
区
域
D
按
图
1
分
4
部
分
,
得
I
=
∫
−
2
−
1
d
x
∫
−
4
−
x
2
4
−
x
2
f
(
x
,
y
)
d
y
+
∫
−
1
1
d
x
∫
1
−
x
2
4
−
x
2
f
(
x
,
y
)
d
y
+
∫
−
1
1
d
x
∫
−
4
−
x
2
−
1
−
x
2
f
(
x
,
y
)
d
y
+
∫
1
2
d
x
∫
−
4
−
x
2
4
−
x
2
f
(
x
,
y
)
d
y
,
将
积
分
区
域
D
按
图
2
分
4
部
分
,
得
I
=
∫
−
2
1
d
y
∫
−
4
−
y
2
4
−
y
2
f
(
x
,
y
)
d
x
+
∫
−
1
1
d
y
∫
−
4
−
y
2
−
1
−
y
2
f
(
x
,
y
)
d
x
+
∫
−
1
1
d
y
∫
1
−
y
2
4
−
y
2
f
(
x
,
y
)
d
x
+
∫
1
2
d
y
∫
−
4
−
y
2
4
−
y
2
f
(
x
,
y
)
d
x
.
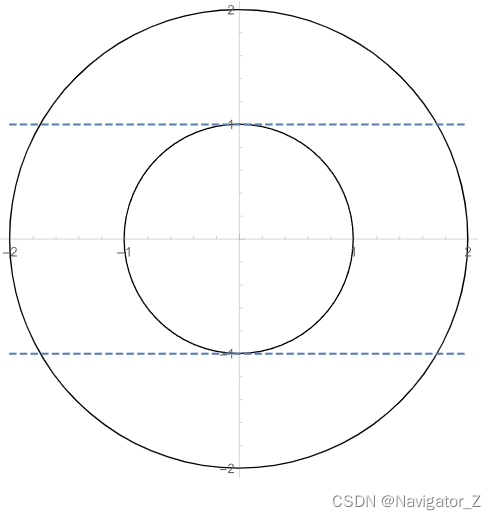
begin{aligned} & (4) 将积分区域D按图1分4部分,得I=\\ & int_{-2}^{-1}dxint_{-sqrt{4-x^2}}^{sqrt{4-x^2}}f(x, y)dy+int_{-1}^{1}dxint_{sqrt{1-x^2}}^{sqrt{4-x^2}}f(x, y)dy+int_{-1}^{1}dxint_{-sqrt{4-x^2}}^{-sqrt{1-x^2}}f(x, y)dy+int_{1}^{2}dxint_{-sqrt{4-x^2}}^{sqrt{4-x^2}}f(x, y)dy,\\ & 将积分区域D按图2分4部分,得I=\\ & int_{-2}^{1}dyint_{-sqrt{4-y^2}}^{sqrt{4-y^2}}f(x, y)dx+int_{-1}^{1}dyint_{-sqrt{4-y^2}}^{-sqrt{1-y^2}}f(x, y)dx+int_{-1}^{1}dyint_{sqrt{1-y^2}}^{sqrt{4-y^2}}f(x, y)dx+int_{1}^{2}dyint_{-sqrt{4-y^2}}^{sqrt{4-y^2}}f(x, y)dx. & end{aligned}
(4) 将积分区域D按图1分4部分,得I= ∫−2−1dx∫−4−x24−x2f(x, y)dy+∫−11dx∫1−x24−x2f(x, y)dy+∫−11dx∫−4−x2−1−x2f(x, y)dy+∫12dx∫−4−x24−x2f(x, y)dy, 将积分区域D按图2分4部分,得I= ∫−21dy∫−4−y24−y2f(x, y)dx+∫−11dy∫−4−y2−1−y2f(x, y)dx+∫−11dy∫1−y24−y2f(x, y)dx+∫12dy∫−4−y24−y2f(x, y)dx.
5. 设 f ( x , y ) 在 D 上 连 续 , 其 中 D 是 由 直 线 y = x 、 y = a 及 x = b ( b > a ) 所 围 成 的 闭 区 域 , 证 明 ∫ a b d x ∫ a x f ( x , y ) d y = ∫ a b d y ∫ y b f ( x , y ) d x . begin{aligned}&5. 设f(x, y)在D上连续,其中D是由直线y=x、y=a及x=b(b gt a)所围成的闭区域,证明\\& int_{a}^{b}dxint_{a}^{x}f(x, y)dy=int_{a}^{b}dyint_{y}^{b}f(x, y)dx.&end{aligned} 5. 设f(x, y)在D上连续,其中D是由直线y=x、y=a及x=b(b>a)所围成的闭区域,证明 ∫abdx∫axf(x, y)dy=∫abdy∫ybf(x, y)dx.
解:
等 式 两 端 的 二 次 积 分 都 等 于 二 重 积 分 ∬ D f ( x , y ) d σ , 因 此 两 端 相 等 . begin{aligned} & 等式两端的二次积分都等于二重积分iint_{D}f(x, y)dsigma,因此两端相等. & end{aligned} 等式两端的二次积分都等于二重积分∬Df(x, y)dσ,因此两端相等.
6. 改 换 下 列 二 次 积 分 的 积 分 次 序 : begin{aligned}&6. 改换下列二次积分的积分次序:&end{aligned} 6. 改换下列二次积分的积分次序:
( 1 ) ∫ 0 1 d y ∫ 0 y f ( x , y ) d x ; ( 2 ) ∫ 0 2 d y ∫ y 2 2 y f ( x , y ) d x ; ( 3 ) ∫ 0 1 d y ∫ − 1 − y 2 1 − y 2 f ( x , y ) d x ; ( 4 ) ∫ 1 2 ∫ 2 − x 2 x − x 2 f ( x , y ) d y ; ( 5 ) ∫ 1 e d x ∫ 0 l n x f ( x , y ) d y ; ( 6 ) ∫ 0 π d x ∫ − s i n x 2 s i n x f ( x , y ) d y . begin{aligned} & (1) int_{0}^{1}dyint_{0}^{y}f(x, y)dx; (2) int_{0}^{2}dyint_{y^2}^{2y}f(x, y)dx;\\ & (3) int_{0}^{1}dyint_{-sqrt{1-y^2}}^{sqrt{1-y^2}}f(x, y)dx; (4) int_{1}^{2}int_{2-x}^{sqrt{2x-x^2}}f(x, y)dy;\\ & (5) int_{1}^{e}dxint_{0}^{ln x}f(x, y)dy; (6) int_{0}^{pi}dxint_{-sin frac{x}{2}}^{sin x}f(x, y)dy. & end{aligned} (1) ∫01dy∫0yf(x, y)dx; (2) ∫02dy∫y22yf(x, y)dx; (3) ∫01dy∫−1−y21−y2f(x, y)dx; (4) ∫12∫2−x2x−x2f(x, y)dy; (5) ∫1edx∫0ln xf(x, y)dy; (6) ∫0πdx∫−sin 2xsin xf(x, y)dy.
解:
(
1
)
二
次
积
分
等
于
二
重
积
分
∬
D
f
(
x
,
y
)
d
σ
,
其
中
D
=
{
(
x
,
y
)
∣
0
≤
x
≤
y
,
0
≤
y
≤
1
}
,
D
又
可
表
示
为
{
(
x
,
y
)
∣
x
≤
y
≤
1
,
0
≤
x
≤
1
}
,
则
∫
0
1
d
y
∫
0
y
f
(
x
,
y
)
d
x
=
∫
0
1
d
x
∫
x
1
f
(
x
,
y
)
d
y
.
begin{aligned} & (1) 二次积分等于二重积分iint_{D}f(x, y)dsigma,其中D={(x, y) | 0 le x le y,0 le y le 1},\\ & D又可表示为{(x, y) | x le y le 1,0 le x le 1},则int_{0}^{1}dyint_{0}^{y}f(x, y)dx=int_{0}^{1}dxint_{x}^{1}f(x, y)dy.\\ & end{aligned}
(1) 二次积分等于二重积分∬Df(x, y)dσ,其中D={(x, y) ∣ 0≤x≤y,0≤y≤1}, D又可表示为{(x, y) ∣ x≤y≤1,0≤x≤1},则∫01dy∫0yf(x, y)dx=∫01dx∫x1f(x, y)dy.
(
2
)
二
次
积
分
等
于
二
重
积
分
∬
D
f
(
x
,
y
)
d
σ
,
其
中
D
=
{
(
x
,
y
)
∣
y
2
≤
x
≤
2
y
,
0
≤
y
≤
2
}
,
D
又
可
表
示
为
{
(
x
,
y
)
∣
x
2
≤
y
≤
x
,
0
≤
x
≤
4
}
,
则
∫
0
2
d
y
∫
y
2
2
y
f
(
x
,
y
)
d
x
=
∫
0
4
d
x
∫
x
2
x
f
(
x
,
y
)
d
y
.
begin{aligned} & (2) 二次积分等于二重积分iint_{D}f(x, y)dsigma,其中D={(x, y) | y^2 le x le 2y,0 le y le 2},\\ & D又可表示为{(x, y) | frac{x}{2} le y le sqrt{x},0 le x le 4},则int_{0}^{2}dyint_{y^2}^{2y}f(x, y)dx=int_{0}^{4}dxint_{frac{x}{2}}^{sqrt{x}}f(x, y)dy.\\ & end{aligned}
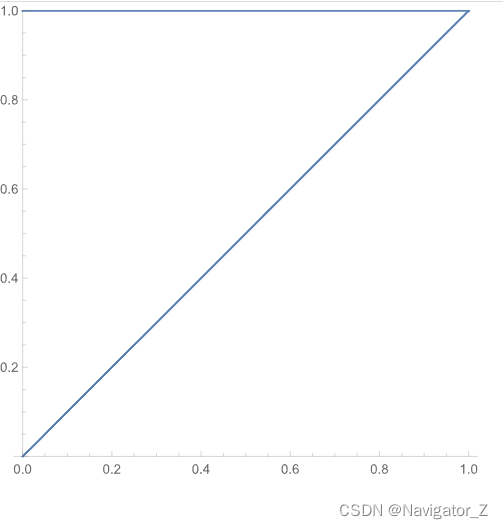
(2) 二次积分等于二重积分∬Df(x, y)dσ,其中D={(x, y) ∣ y2≤x≤2y,0≤y≤2}, D又可表示为{(x, y) ∣ 2x≤y≤x,0≤x≤4},则∫02dy∫y22yf(x, y)dx=∫04dx∫2xxf(x, y)dy.
(
3
)
二
次
积
分
等
于
二
重
积
分
∬
D
f
(
x
,
y
)
d
σ
,
其
中
D
=
{
(
x
,
y
)
∣
−
1
−
y
2
≤
x
≤
1
−
y
2
,
0
≤
y
≤
1
}
,
D
又
可
表
示
为
{
(
x
,
y
)
∣
0
≤
y
≤
1
−
x
2
,
−
1
≤
x
≤
1
}
,
则
∫
0
1
d
y
∫
−
1
−
y
2
1
−
y
2
f
(
x
,
y
)
d
x
=
∫
−
1
1
d
x
∫
0
1
−
x
2
f
(
x
,
y
)
d
y
.
begin{aligned} & (3) 二次积分等于二重积分iint_{D}f(x, y)dsigma,其中D={(x, y) | -sqrt{1-y^2} le x le sqrt{1-y^2},0 le y le 1},\\ & D又可表示为{(x, y) | 0 le y le sqrt{1-x^2},-1 le x le 1},\\ & 则int_{0}^{1}dyint_{-sqrt{1-y^2}}^{sqrt{1-y^2}}f(x, y)dx=int_{-1}^{1}dxint_{0}^{sqrt{1-x^2}}f(x, y)dy.\\ & end{aligned}
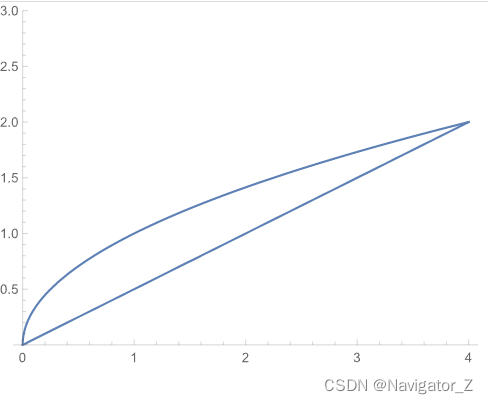
(3) 二次积分等于二重积分∬Df(x, y)dσ,其中D={(x, y) ∣ −1−y2≤x≤1−y2,0≤y≤1}, D又可表示为{(x, y) ∣ 0≤y≤1−x2,−1≤x≤1}, 则∫01dy∫−1−y21−y2f(x, y)dx=∫−11dx∫01−x2f(x, y)dy.
(
4
)
二
次
积
分
等
于
二
重
积
分
∬
D
f
(
x
,
y
)
d
σ
,
其
中
D
=
{
(
x
,
y
)
∣
2
−
x
≤
y
≤
2
x
−
x
2
,
1
≤
x
≤
2
}
,
D
又
可
表
示
为
{
(
x
,
y
)
∣
2
−
y
≤
x
≤
1
+
1
−
y
2
,
0
≤
y
≤
1
}
,
则
∫
1
2
∫
2
−
x
2
x
−
x
2
f
(
x
,
y
)
d
y
=
∫
0
1
d
y
∫
2
−
y
1
+
1
−
y
2
f
(
x
,
y
)
d
x
.
begin{aligned} & (4) 二次积分等于二重积分iint_{D}f(x, y)dsigma,其中D={(x, y) | 2-x le y le sqrt{2x-x^2},1 le x le 2},\\ & D又可表示为{(x, y) | 2-y le x le 1+sqrt{1-y^2},0 le y le 1},\\ & 则int_{1}^{2}int_{2-x}^{sqrt{2x-x^2}}f(x, y)dy=int_{0}^{1}dyint_{2-y}^{1+sqrt{1-y^2}}f(x, y)dx.\\ & end{aligned}
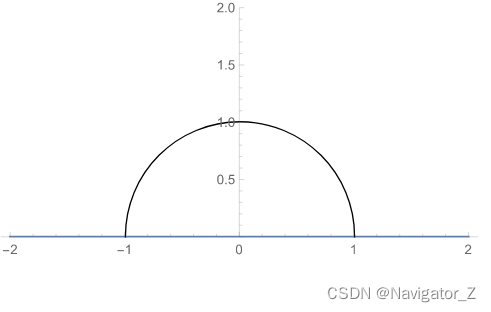
(4) 二次积分等于二重积分∬Df(x, y)dσ,其中D={(x, y) ∣ 2−x≤y≤2x−x2,1≤x≤2}, D又可表示为{(x, y) ∣ 2−y≤x≤1+1−y2,0≤y≤1}, 则∫12∫2−x2x−x2f(x, y)dy=∫01dy∫2−y1+1−y2f(x, y)dx.
(
5
)
二
次
积
分
等
于
二
重
积
分
∬
D
f
(
x
,
y
)
d
σ
,
其
中
D
=
{
(
x
,
y
)
∣
0
≤
y
≤
l
n
x
,
1
≤
x
≤
e
}
,
D
又
可
表
示
为
{
(
x
,
y
)
∣
e
y
≤
x
≤
e
,
0
≤
y
≤
1
}
,
则
∫
1
e
d
x
∫
0
l
n
x
f
(
x
,
y
)
d
y
=
∫
0
1
d
y
∫
e
y
e
f
(
x
,
y
)
d
x
.
begin{aligned} & (5) 二次积分等于二重积分iint_{D}f(x, y)dsigma,其中D={(x, y) | 0 le y le ln x,1 le x le e},\\ & D又可表示为{(x, y) | e^y le x le e,0 le y le 1},\\ & 则int_{1}^{e}dxint_{0}^{ln x}f(x, y)dy=int_{0}^{1}dyint_{e^y}^{e}f(x, y)dx.\\ & end{aligned}
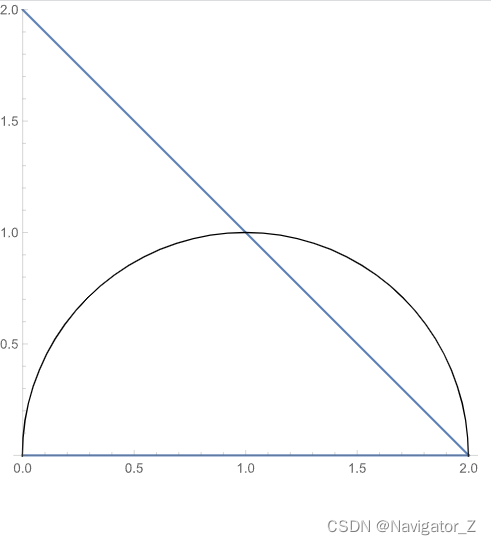
(5) 二次积分等于二重积分∬Df(x, y)dσ,其中D={(x, y) ∣ 0≤y≤ln x,1≤x≤e}, D又可表示为{(x, y) ∣ ey≤x≤e,0≤y≤1}, 则∫1edx∫0ln xf(x, y)dy=∫01dy∫eyef(x, y)dx.
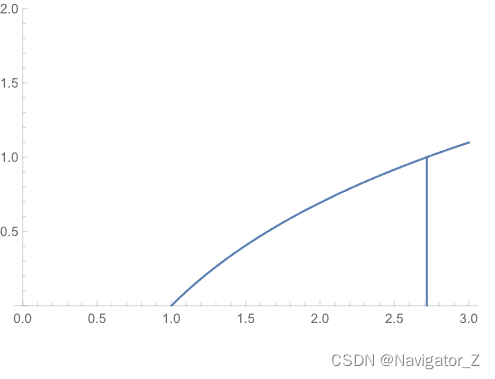
(
6
)
将
积
分
区
域
D
表
示
为
D
1
∪
D
2
,
其
中
D
1
=
{
(
x
,
y
)
∣
a
r
c
s
i
n
y
≤
x
≤
π
−
a
r
c
s
i
n
y
,
0
≤
y
≤
1
}
,
D
2
=
{
(
x
,
y
)
∣
−
2
a
r
c
s
i
n
y
≤
x
≤
π
,
−
1
≤
y
≤
0
}
,
则
∫
0
π
d
x
∫
−
s
i
n
x
2
s
i
n
x
f
(
x
,
y
)
d
y
=
∫
0
1
d
y
∫
a
r
c
s
i
n
y
π
−
a
r
c
s
i
n
y
f
(
x
,
y
)
d
x
+
∫
−
1
0
d
y
∫
−
2
a
r
c
s
i
n
y
π
f
(
x
,
y
)
d
x
.
begin{aligned} & (6) 将积分区域D表示为D_1 cup D_2,其中D_1={(x, y) | arcsin y le x le pi-arcsin y,0 le y le 1},\\ & D_2={(x, y) | -2arcsin y le x le pi,-1 le y le 0},\\ & 则int_{0}^{pi}dxint_{-sin frac{x}{2}}^{sin x}f(x, y)dy=int_{0}^{1}dyint_{arcsin y}^{pi-arcsin y}f(x, y)dx+int_{-1}^{0}dyint_{-2arcsin y}^{pi}f(x, y)dx. & end{aligned}
(6) 将积分区域D表示为D1∪D2,其中D1={(x, y) ∣ arcsin y≤x≤π−arcsin y,0≤y≤1}, D2={(x, y) ∣ −2arcsin y≤x≤π,−1≤y≤0}, 则∫0πdx∫−sin 2xsin xf(x, y)dy=∫01dy∫arcsin yπ−arcsin yf(x, y)dx+∫−10dy∫−2arcsin yπf(x, y)dx.
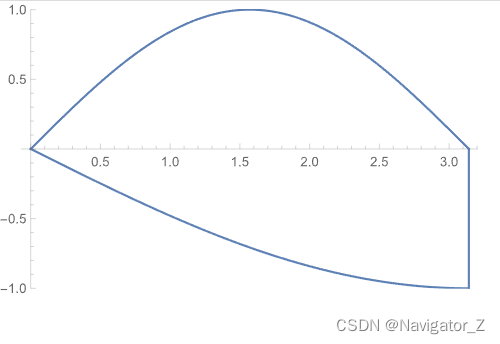
7. 设 平 面 薄 片 所 占 的 闭 区 域 D 由 直 线 x + y = 2 , y = x 和 x 轴 所 围 成 , 它 的 面 密 度 μ ( x , y ) = x 2 + y 2 , 求 该 薄 片 的 质 量 . begin{aligned}&7. 设平面薄片所占的闭区域D由直线x+y=2,y=x和x轴所围成,它的面密度mu(x, y)=x^2+y^2,\\& 求该薄片的质量.&end{aligned} 7. 设平面薄片所占的闭区域D由直线x+y=2,y=x和x轴所围成,它的面密度μ(x, y)=x2+y2, 求该薄片的质量.
解:
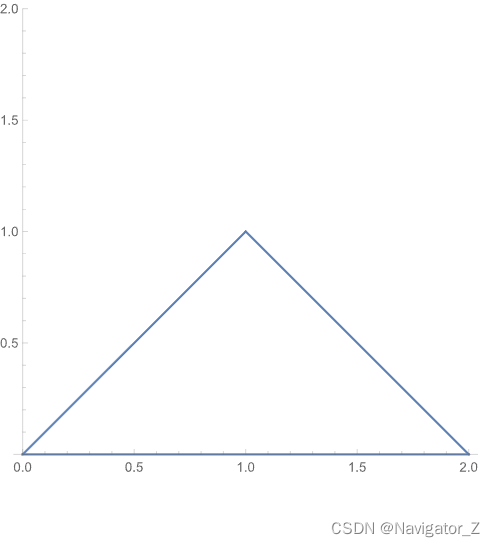
积
分
区
域
D
如
图
所
示
,
设
该
薄
片
质
量
为
M
,
M
=
∬
D
μ
(
x
,
y
)
d
σ
=
∫
0
1
d
y
∫
y
2
−
y
(
x
2
+
y
2
)
d
x
=
∫
0
1
[
1
3
x
3
+
x
y
2
]
y
2
−
y
d
y
=
∫
0
1
[
1
3
(
2
−
y
)
3
+
2
y
2
−
7
3
y
3
]
d
y
=
[
−
1
12
(
2
−
y
)
4
+
2
3
y
3
−
7
12
y
4
]
0
1
=
4
3
.
begin{aligned} & 积分区域D如图所示,设该薄片质量为M,\\ & M=iint_{D}mu(x, y)dsigma=int_{0}^{1}dyint_{y}^{2-y}(x^2+y^2)dx=int_{0}^{1}left[frac{1}{3}x^3+xy^2right]_{y}^{2-y}dy=int_{0}^{1}left[frac{1}{3}(2-y)^3+2y^2-frac{7}{3}y^3right]dy=\\ & left[-frac{1}{12}(2-y)^4+frac{2}{3}y^3-frac{7}{12}y^4right]_{0}^{1}=frac{4}{3}. & end{aligned}
积分区域D如图所示,设该薄片质量为M, M=∬Dμ(x, y)dσ=∫01dy∫y2−y(x2+y2)dx=∫01[31x3+xy2]y2−ydy=∫01[31(2−y)3+2y2−37y3]dy= [−121(2−y)4+32y3−127y4]01=34.
8. 计 算 由 四 个 平 面 x = 0 , y = 0 , x = 1 , y = 1 所 围 成 的 柱 体 被 平 面 z = 0 及 2 x + 3 y + z = 6 截 得 的 立 体 的 体 积 . begin{aligned}&8. 计算由四个平面x=0,y=0,x=1,y=1所围成的柱体被平面z=0及2x+3y+z=6截得的\\& 立体的体积.&end{aligned} 8. 计算由四个平面x=0,y=0,x=1,y=1所围成的柱体被平面z=0及2x+3y+z=6截得的 立体的体积.
解:
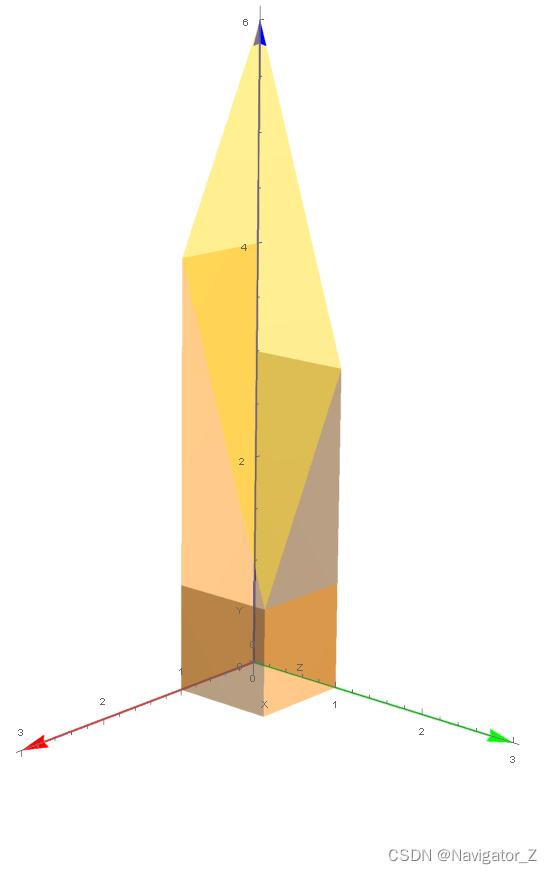
此
立
体
为
一
曲
顶
柱
体
,
底
为
x
O
y
面
上
的
闭
区
域
D
=
{
(
x
,
y
)
∣
0
≤
x
≤
1
,
0
≤
y
≤
1
}
,
顶
为
曲
面
z
=
6
−
2
x
−
3
y
,
所
求
立
体
体
积
为
V
=
∬
D
(
6
−
2
x
−
3
y
)
d
x
d
y
=
∫
0
1
d
x
∫
0
1
(
6
−
2
x
−
3
y
)
d
y
=
∫
0
1
(
9
2
−
2
x
)
d
x
=
7
2
.
begin{aligned} & 此立体为一曲顶柱体,底为xOy面上的闭区域D={(x, y) | 0 le x le 1,0 le y le 1},顶为曲面z=6-2x-3y,\\ & 所求立体体积为V=iint_{D}(6-2x-3y)dxdy=int_{0}^{1}dxint_{0}^{1}(6-2x-3y)dy=int_{0}^{1}left(frac{9}{2}-2xright)dx=frac{7}{2}. & end{aligned}
此立体为一曲顶柱体,底为xOy面上的闭区域D={(x, y) ∣ 0≤x≤1,0≤y≤1},顶为曲面z=6−2x−3y, 所求立体体积为V=∬D(6−2x−3y)dxdy=∫01dx∫01(6−2x−3y)dy=∫01(29−2x)dx=27.
9. 求 由 平 面 x = 0 , y = 0 , x + y = 1 所 围 成 的 柱 体 被 平 面 z = 0 及 抛 物 面 x 2 + y 2 = 6 − z 截 得 的 立 体 的 体 积 . begin{aligned}&9. 求由平面x=0,y=0,x+y=1所围成的柱体被平面z=0及抛物面x^2+y^2=6-z截得的立体的体积.&end{aligned} 9. 求由平面x=0,y=0,x+y=1所围成的柱体被平面z=0及抛物面x2+y2=6−z截得的立体的体积.
解:
此
立
体
为
曲
顶
柱
体
,
底
为
x
O
y
面
上
的
闭
区
域
D
=
{
(
x
,
y
)
∣
0
≤
y
≤
1
−
x
,
0
≤
x
≤
1
}
,
顶
为
曲
面
z
=
6
−
(
x
2
+
y
2
)
,
体
积
为
V
=
∬
D
[
6
−
(
x
2
+
y
2
)
]
d
x
d
y
=
∫
0
1
d
x
∫
0
1
−
x
(
6
−
x
2
−
y
2
)
d
y
=
∫
0
1
[
6
(
1
−
x
)
−
x
2
+
x
3
−
1
3
(
1
−
x
)
3
]
d
x
=
17
6
.
begin{aligned} & 此立体为曲顶柱体,底为xOy面上的闭区域D={(x, y) | 0 le y le 1-x,0 le x le 1},顶为曲面z=6-(x^2+y^2),\\ & 体积为V=iint_{D}[6-(x^2+y^2)]dxdy=int_{0}^{1}dxint_{0}^{1-x}(6-x^2-y^2)dy=int_{0}^{1}left[6(1-x)-x^2+x^3-frac{1}{3}(1-x)^3right]dx=frac{17}{6}. & end{aligned}
此立体为曲顶柱体,底为xOy面上的闭区域D={(x, y) ∣ 0≤y≤1−x,0≤x≤1},顶为曲面z=6−(x2+y2), 体积为V=∬D[6−(x2+y2)]dxdy=∫01dx∫01−x(6−x2−y2)dy=∫01[6(1−x)−x2+x3−31(1−x)3]dx=617.
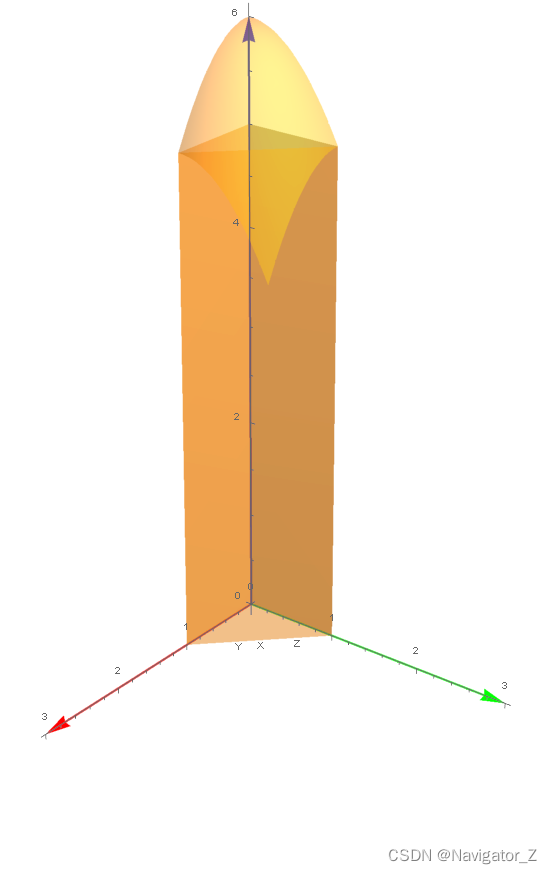
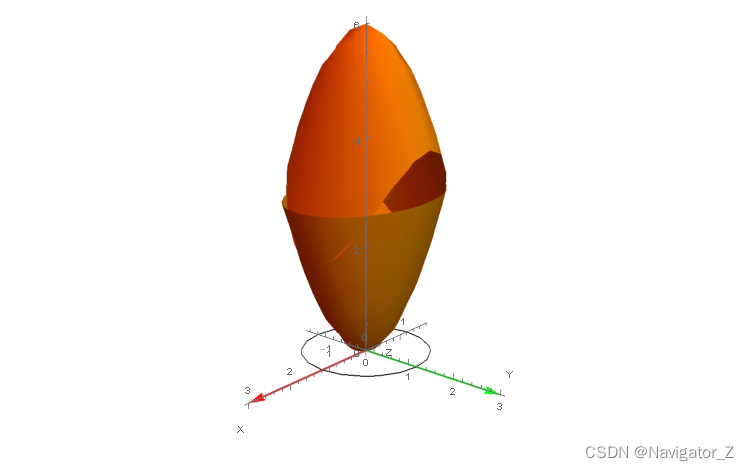
10. 求 由 曲 面 z = x 2 + 2 y 2 及 z = 6 − 2 x 2 − y 2 所 围 成 的 立 体 的 体 积 . begin{aligned}&10. 求由曲面z=x^2+2y^2及z=6-2x^2-y^2所围成的立体的体积.&end{aligned} 10. 求由曲面z=x2+2y2及z=6−2x2−y2所围成的立体的体积.
解:
联
立
方
程
组
{
z
=
x
2
+
2
y
2
,
z
=
6
−
2
x
2
−
y
2
得
x
2
+
y
2
=
2
,
所
求
立
体
在
x
O
y
面
上
的
投
影
区
域
为
D
=
{
(
x
,
y
)
∣
x
2
+
y
2
≤
2
}
,
所
求
立
体
的
体
积
等
于
两
个
曲
顶
柱
体
体
积
的
差
,
V
=
∬
D
(
6
−
2
x
2
−
y
2
)
d
σ
−
∬
D
(
x
2
+
2
y
2
)
d
σ
=
∬
D
(
6
−
3
x
2
−
3
y
2
)
d
σ
=
∬
D
(
6
−
3
ρ
2
)
ρ
d
ρ
d
θ
=
∫
0
2
π
d
θ
∫
0
2
(
6
−
3
ρ
2
)
ρ
d
ρ
=
6
π
.
begin{aligned} & 联立方程组begin{cases}z=x^2+2y^2,\\z=6-2x^2-y^2end{cases}得x^2+y^2=2,所求立体在xOy面上的投影区域为D={(x, y) | x^2+y^2 le 2},\\ & 所求立体的体积等于两个曲顶柱体体积的差,V=iint_{D}(6-2x^2-y^2)dsigma-iint_{D}(x^2+2y^2)dsigma=\\ & iint_{D}(6-3x^2-3y^2)dsigma=iint_{D}(6-3rho^2)rho drho dtheta=int_{0}^{2pi}dtheta int_{0}^{sqrt{2}}(6-3rho^2)rho drho=6pi. & end{aligned}
联立方程组⎩⎪⎨⎪⎧z=x2+2y2,z=6−2x2−y2得x2+y2=2,所求立体在xOy面上的投影区域为D={(x, y) ∣ x2+y2≤2}, 所求立体的体积等于两个曲顶柱体体积的差,V=∬D(6−2x2−y2)dσ−∬D(x2+2y2)dσ= ∬D(6−3x2−3y2)dσ=∬D(6−3ρ2)ρdρdθ=∫02πdθ∫02(6−3ρ2)ρdρ=6π.
最后
以上就是苗条可乐最近收集整理的关于高等数学(第七版)同济大学 习题10-2(前10题) 个人解答的全部内容,更多相关高等数学(第七版)同济大学内容请搜索靠谱客的其他文章。








发表评论 取消回复