概述
最小编辑距离(Minimum Edit Distance)本身是的一个NLP中的一个概念,最小编辑距离旨在定义两个字符串之间的相似度(word similarity)。定义相似度可以用于拼写纠错,计算生物学上的序列比对,机器翻译,信息提取,语音识别等。
编辑距离
两个字符串之间有多相似?
在搜索引擎中,我们总会有偶尔拼错单词的情况,但我们会发现,即便我们拼错了,搜索引擎也能正确地显示出我们想要的结果,而且还会温馨地给出拼写错误的提示。
如果我们在Google中检索”Gooogle”,我们会看到如下结果。
Showing results for google
Search instead for gooogle
Google知道我们输错了,但是它是怎么知道我们输错的呢?
同样地,在生物学中,我们想知道两段DNA或者RNA的有多相似,也会遇到类似的问题。
Seq1: AGGCTATCACCTGACCTCCAGGCCGATGCCC
Seq2: TAGCTATCACGACCGCGGTCGATTTGCCCGAC
对比结果:
Seq1: -AGGCTATCACCTGACCTCCAGGCCGA–TGCCC—
Seq2: TAG-CTATCAC–GACCGC–GGTCGATTTGCCCGAC
同样类似的场景还有很多,我们可以从中抽取出一个共通的问题,即从一个字符串转变为另一个字符串,需要经过怎样的编辑操作。
编辑距离和最小编辑距离
为了解决该问题,我们引入了编辑距离的概念,所谓的编辑距离,就是从串A转换到串B所需的编辑操作次数。
这里的编辑操作包括:
- 插入
- 删除
- 替换
而最小编辑距离(Minimum Edit Distance)就很容易理解了,就是从串A转换到串B所需的最少编辑操作次数(对应的代价)之和。
现在我们来考虑intention和execution两个单词之间的编辑距离。
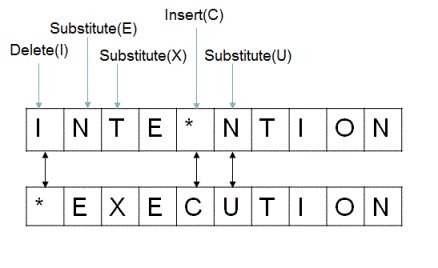
从上表可以看出,从intention到execution需要1次删除,3次替换,和1次插入。
如果我们把三种操作的代价都记为1,则其编辑距离为5。
除此之外还有一种计算方法将替换的记为2(即一次删除和一次插入),这种距离也被称为列文斯坦(Levenshtein)距离,此时的总距离为8。
动态规划求解MED
算法思想及伪码描述
求解MED最常用的方法采用了动态规规划的思想,计算过程中通过构建一张编辑距离表的方式,将串X到串Y的每一个编辑状态计算出来,每一步计算状态依赖于之前的计算状态。
# 伪码描述
D(i, 0) = i;
D(0, j) = j;
For each i = 1...M
For each j = 1...N
d1 = D(i - 1, j) + 1
d2 = D(i, j - 1) + 1
d3 = D(i - 1, j - 1) + X(i) === Y (j) ? 0 : 2
D(i, j) = min(d1, d2, d3)其中D(n, m)是距离,X(i)表示串X第i个位置的字符,Y(j)表示串Y第j个位置的字符。
编辑距离表
通过上述思想,我们可以构建一张编辑距离表。
首先初始化的时候其距离为,表的状态为:
| N | 9 | |||||||||
| O | 8 | |||||||||
| I | 7 | |||||||||
| T | 6 | |||||||||
| N | 5 | |||||||||
| E | 4 | |||||||||
| T | 3 | |||||||||
| N | 2 | |||||||||
| I | 1 | |||||||||
| # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| # | E | X | E | C | U | T | I | O | N |
怎么理解这个表呢?
我们从倒数第二行开始,其第一列为#,表示一个空字符串,#到#对应的值为0,表示从一个空字符串到一个空字符串的MED为0。
#到E对应的值为1,表示从空字符串到E的MED为1,#到X对应的值为2,表示从空字符串到EX的MED为2,以此类推。
反过来,从第二列由下往上推也是同理。
现在我们完成了编辑距离表的初始化,接下来要完成整个表的填充。
实际上对于第D(n, m)的计算在伪码的描述中已经很明确了,就是求三个数值的最小值,第一个数值是表中当前位置的左边的数值 + 1,第二个数值是当前位置下面的数值 + 1,第三个数值相对复杂一点,如果当前位置对应的两个字符一样,则第三个数值就是左下角的数值,表示不需要做任何编辑,否则的话左下角的数字 + 2,表示是一次替换操作(这里认为一次替换操作的代价是2)。
现在我们来求倒数第三行第三列的数值,从上表可以看出,d1 = 1 + 1,d2 = 1 + 1,d3 = 0 + 2,三个值的最小值为2,所以D(0, 0) = 2。
| N | 9 | |||||||||
| O | 8 | |||||||||
| I | 7 | |||||||||
| T | 6 | |||||||||
| N | 5 | |||||||||
| E | 4 | |||||||||
| T | 3 | |||||||||
| N | 2 | |||||||||
| I | 1 | 2 | ||||||||
| # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| # | E | X | E | C | U | T | I | O | N |
同样的道理可以求出,D(1, 2) = min(2 + 1, 2 + 1, 1 + 2),即3。
一直这样计算我们可以得出:
| N | 9 | |||||||||
| O | 8 | |||||||||
| I | 7 | |||||||||
| T | 6 | |||||||||
| N | 5 | |||||||||
| E | 4 | |||||||||
| T | 3 | |||||||||
| N | 2 | |||||||||
| I | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 6 | ||
| # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| # | E | X | E | C | U | T | I | O | N |
接下来我们计算D(0, 6),可以发现X(0)和Y(6)是相同的,都是'I',所以这里的值应该是min(7 + 1, 7 + 1, 6 + 0),即6。
一次类推,我们可以将整个编辑距离表计算出来。
| N | 9 | 8 | 9 | 10 | 11 | 12 | 11 | 10 | 9 | 8 |
| O | 8 | 7 | 8 | 9 | 10 | 11 | 10 | 9 | 8 | 9 |
| I | 7 | 6 | 7 | 8 | 9 | 10 | 9 | 8 | 9 | 10 |
| T | 6 | 5 | 6 | 7 | 8 | 9 | 8 | 9 | 10 | 11 |
| N | 5 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 10 |
| E | 4 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 9 |
| T | 3 | 4 | 5 | 6 | 7 | 8 | 7 | 8 | 9 | 8 |
| N | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 7 | 8 | 7 |
| I | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 6 | 7 | 8 |
| # | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| # | E | X | E | C | U | T | I | O | N |
最终可以算出表中右上角的数值是8,也就是说从INTENTION到EXECUTION的最小编辑距离为8。
带追溯过程的最小编辑编辑
求得最小编辑距离的值是不够的,我们还可以将整个过程回溯的过程记录下来,即我们是怎么计算出8这个值的。
| N | 9↓ | 8↓ | 9←↙↓ | 10←↙↓ | 11←↙↓ | 12←↙↓ | 11↓ | 10↓ | 9↓ | 8↙ |
| O | 8↓ | 7↓ | 8←↙↓ | 9←↙↓ | 10←↙↓ | 11←↙↓ | 10↓ | 9↓ | 8↙ | 9← |
| I | 7↓ | 6↓ | 7←↙↓ | 8←↙↓ | 9←↙↓ | 10←↙↓ | 9↓ | 8↙ | 9← | 10← |
| T | 6↓ | 5↓ | 6←↙↓ | 7←↙↓ | 8←↙↓ | 9←↙↓ | 8↙ | 9← | 10← | 11←↓ |
| N | 5↓ | 4↓ | 5←↙↓ | 6←↙↓ | 7←↙↓ | 8←↙↓ | 9←↙↓ | 10←↙↓ | 11←↙↓ | 10↙↓ |
| E | 4↓ | 3↙ | 4↙ | 5↙ | 6← | 7← | 8←↓ | 9←↙↓ | 10←↙↓ | 9↓ |
| T | 3↓ | 4←↙↓ | 5←↙↓ | 6←↙↓ | 7←↙↓ | 8←↙↓ | 7↙ | 8←↓ | 9←↙↓ | 8↓ |
| N | 2↓ | 3←↙↓ | 4←↙↓ | 5←↙↓ | 6←↙↓ | 7←↙↓ | 8←↙↓ | 7↙↓ | 8←↙↓ | 7↙ |
| I | 1↓ | 2←↙↓ | 3←↙↓ | 4←↙↓ | 5←↙↓ | 6←↙↓ | 7←↙↓ | 6↙ | 7← | 8← |
| # | 0 | 1← | 2← | 3← | 4← | 5← | 6← | 7← | 8← | 9← |
| # | E | X | E | C | U | T | I | O | N |
这样我们可以记录一整个编辑过程。
从上图的右上角开始,我们可以划出一条完整的追溯路径。
下表是从右向左填写的。
| X | I | N | T | E | - | N | T | I | O | N |
| Y | - | E | X | E | C | U | T | I | O | N |
| Action | Delete | Substitute | Substitute | Insert | Substitute |
是不是和本文一开始的那张图一模一样呢?
1次删除,3次替换,和1次插入,编辑距离正好是8。
C++实现
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(),m = word2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1));
for(int i = 0;i <= n; ++i) dp[i][0] = i;
for(int j = 0;j <= m; ++j) dp[0][j] = j;
for(int i = 1;i<=n;++i){
for(int j = 1;j<=m;++j){
if(word1[i-1] == word2[j-1])
dp[i][j] = dp[i-1][j-1];
else
dp[i][j] = 1 +min(dp[i-1][j-1],min(dp[i][j-1],dp[i-1][j]));
}
}
return dp[n][m];
}
};总结
最小编辑距离还有一种加权最小编辑距离的形式,用于处理某些改动频率不一的情况,本文不再赘述,感兴趣的同学可以查看参考1。
参考
- Minimum Edit Distance - Dan Jurafsky - Stanford
- 深度剖析:如何实现一个 Virtual DOM 算法 - livoras
最后
以上就是自然路人最近收集整理的关于动态规划之最小编辑距离的全部内容,更多相关动态规划之最小编辑距离内容请搜索靠谱客的其他文章。








发表评论 取消回复