求解字符串间最短距离(字符串相似度)

60 阅读 0 评论 40 点赞

我是靠谱客的博主风趣鸵鸟，最近开发中收集的这篇文章主要介绍求解字符串间最短距离(字符串相似度)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

问题描述：

给定任意两个字符串，比如：str1=“abcd”和str2=“gbcdz”,计算这两个字符串间的相似度。计算两字符串的相似度可等价于计算将str1变换到str2所需要的最少步骤。

问题分析：

为计算将str1变换到str2所需最小操作步骤，必须先对变换操作进行定义：

1.修改一个字符（如把“a”替换为“g”）;

2.增加一个字符（如把“abcd”变为“abcdz”）;

3.删除一个字符（如把“travelling”变为“traveling”）;

字符串变换过程中执行了上述三个操作之间的任一操作，则两字符串间距离就加1。例如将上文中的str1变换到str2，即“abcd”到“gbcdz”，通过“abcd”->（操作1）->“gbcd”->（操作2）->“gbcdz”,需进行一次修改和一次添加字符操作，故两字符串距离为2，那么字符串相似度则为距离+1的倒数，即1/3=0.333。这是由俄罗斯科学家Vladimir Levenshtein在1965年提出这个概念。因此也叫Levenshtein Distance。

那么如果给定两个任意字符串，如何计算它们距离呢？

问题解决：

解决此问题最好的方法是采用动态规划的方法。如下：

设str1=“abcd”，str2=“gbcdz”，定义一个二维数组d[][]，d[i][j]表示str1中取前i个字符和str2中取前j个字符的最短距离，例如d[3][2]表示“abc”到“gb”的最短距离。

d[i][j]的计算规则有三条：

来自d[i - i][j - 1]，即 “str1的前i-1个字符组成的子串” 到 “str2的前j-1个字符组成的子串” 的最小距离，此时如果str1[i] = str2[j]，则最短距离不变，否则最短距离加1（即把str1[i]变为str2[j] ），所以d[i][j] = d[i - 1][j - 1] + (str1[i] == str2[j] ? 0 : 1)
来自d[i - 1][j]，即 “A的前i-1个字符组成的子串” 到 “B的前j个字符组成的子串” 的编辑距离。此时删除在A的第i个位置上的字符即可，所以d[i][j] = d[i - 1][j] + 1
来自d[i][j - 1], 即 “A的前i个字符组成的子串” 到 “B的前j-1个字符组成的子串” 的编辑距离。此时在A的子串后面添加一个字符B[j]即可，所以d[i][j] = d[i][j - 1] + 1

于是状态转移方程：d[i][j] = min (d[i - 1][j - 1] + (str1[i] == str2[j] ? 0 : 1) , d[i - 1][j] + 1 , d[i][j - 1] + 1)

例如str1=“abcd”，str2=“gbcdz”的d[][]就为（注意i，j的取值范围）：

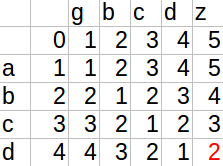
代码实现(anycodex.com在线编译器测试通过，试一试？)：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int min(int a, int b, int c);
int calc(char* a, char* b);
int main(void){
printf("%d",calc("abcd", "gbcdz"));
return EXIT_SUCCESS;
}
int min(int a, int b, int c)
{
if(a > b)
a = b;
if(a > c)
a = c;
return a;
}
int calc(char* a, char* b)
{
int lenA = strlen(a);
int lenB = strlen(b);
int d[lenA+1][lenB+1];
for(int i=0;i<=lenA;++i)
d[i][0] = i;
for(int i=0;i<=lenB;++i)
d[0][i] = i;
for(int i=1;i<=lenA;++i)
for(int j=1;j<=lenB;++j)
d[i][j] = min(d[i-1][j-1] + (a[i-1] == b[j-1] ? 0:1), d[i-1][j]+1, d[i][j-1]+1);
return d[lenA][lenB];
}