概述
文章目录
- 前言
- 一、自适应多阈值分割
- 1.最大类间差方法
- 2.最大熵方法
- 二、代码部分（以粒子群算法与遗传算法优化自适应双阈值分割为例）
- 1. 利用粒子群算法优化最大类间差双阈值分割
- 1.1 概述
- 1.2 代码部分
- 1.3 结果展示
- 2. 利用遗传算法优化最大类间差双阈值分割
- 2.1 概述
- 2.2 代码部分
- 1.3 结果展示
- 三、总结
前言
上次谈到图像的自适应分割问题，具体参考博文【图像分割】自适应阈值图像分割方法（最大类间差法与最大熵法）
但阈值法根据阈值个数可分为单阈值和多阈值分割，即用一个或多个阈值将图像的灰度级分为一个或多个部分。假设一幅图像具有L个灰度级，在多阈值情况下，其区域划分准则为：
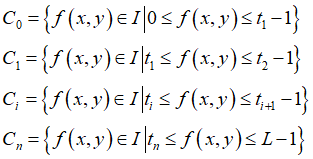
其中，C0,C1,…,Cn是图像划分的不同区域，ti为不同的阈值，n 为阈值数量，f(x,y) 代表图像的任意像素点的灰度级。
之所以用智能优化算法进行自适应多阈值分割的优化，其必要性在于利用优化算法可以在较短的时间内得到最优解，例如利用遍历的方法对最大类间差方法或者最大熵法进行分割，单阈值分割只需要遍历256次，而双阈值分割就需要32640次，三个阈值需要2763520次！！！
可以看出，随着阈值分级的增加，计算的次数爆炸性的增长。
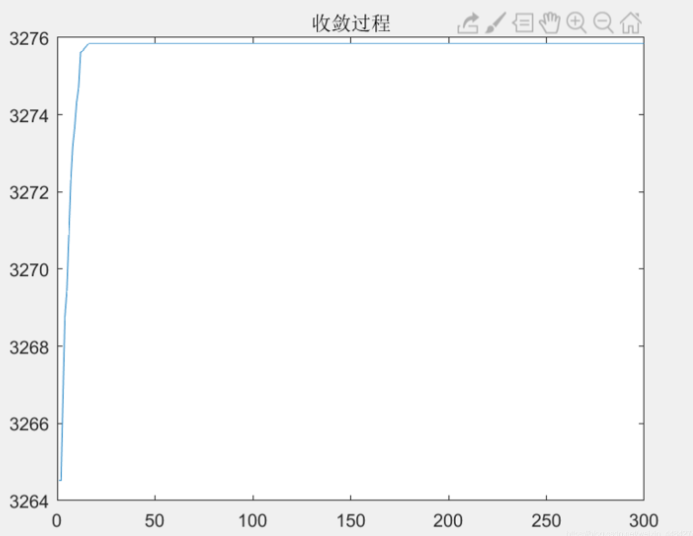
但是利用智能优化算法，三阈值分割可以快速搜索到最优解，如下图为利用粒子群算法进行三阈值分割的收敛曲线，该种群选取500个个体，可以看到迭代20代左右就搜索到了最佳阈值组合，计算次数约为一万次，相较于遍历方法，计算量大大减少。
一、自适应多阈值分割
1.最大类间差方法
2.最大熵方法
二、代码部分（以粒子群算法与遗传算法优化自适应双阈值分割为例）
1. 利用粒子群算法优化最大类间差双阈值分割
1.1 概述
粒子群优化算法 (Particle swarm optimization) 是一种进化计算技术。源于对鸟群捕食的行为研究。粒子群优化算法的基本思想：是通过群体中个体之间的协作和信息共享来寻找最优解。
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。
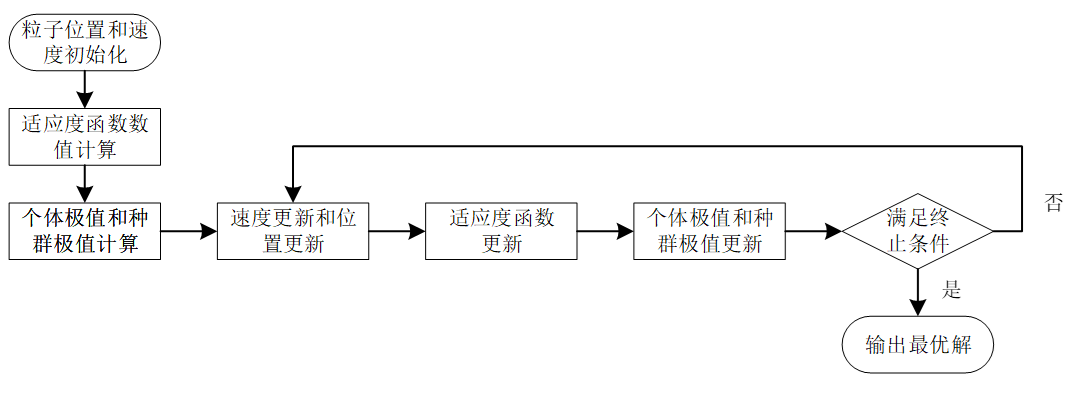下面结合代码来看一下优化过程：
1.2 代码部分
首先输入要处理的图片，并对种群进行基本的定义，同时初始化种群位置。
%% 输入图像；
Imag = imread('24063.jpg');%296059
Imag=rgb2gray(Imag);
Image_OSTU=Imag;
%% 开始种群等基本定义
N = 500; % 初始种群个数
d = 2; % 阈值个数（参看上述的函数表达式）
ger = 300; % 最大迭代次数
plimit = [1,256];
vlimit = [-2.5, 2.5;-2.5, 2.5]; % 设置速度限制
w = 0.8; % 惯性权重,个体历史成绩对现在的影响0.5~1之间
%还有自适应调整权重、随机权重等等
%（不同的权重设置很影响性能，按需要选取）
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子
x = zeros(N, 2);
for i = 1:N %对每一个个体
x(i,1) = floor(plimit(1) + (plimit(2) - plimit(1)) * rand);%初始种群的位置
x(i,2) = floor(x(i,1) + (plimit(2) - x(i,1)) * rand);%初始种群的位置
end
v = rand(N, d); % 初始种群的速度,500行2列分别在两个维度上
xm = x; % 每个个体的历史最佳位置
ym = zeros(1, d); % 种群的历史最佳位置，两个维度，设置为0
fxm = zeros(N, 1); % 每个个体的历史最佳适应度，设置为0
fym = -inf; % 种群历史最佳适应度,求最大值先设置成负无穷
iter=1; %初始的迭代次数因为用while设置为一
times = 1;
record = zeros(ger, 1); %记录器
在进行了种群的基本定义与初始化后，开始对种群进行迭代更新
%% 迭代更新开始
while iter <= ger
fx = f(x); % 代入x中的二维数据，算出个体当前适应度,为500行1列的数据
for i = 1:N %对每一个个体做判断
if fxm(i) < fx(i) %如果每个个体的历史最佳适应度小于个体当前适应度
fxm(i) = fx(i); % 更新个体历史最佳适应度,第一轮就是把小于零的清除
xm(i,:) = x(i,:); % 更新个体历史最佳位置
end
end
if fym < max(fxm) %种群历史最佳适应度小于个体里面最佳适应度的最大值
[fym, nmax] = max(fxm); % 更新群体历史最佳适应度,取出最大适应度的值和所在行数即位置
ym = xm(nmax, :); % 更新群体历史最佳位置
end
v = v * w + c1 * rand *(xm - x) + c2 * rand *(repmat(ym, N, 1) - x);
% 速度更新公式,repmat函数把ym矩阵扩充成N行1列
%%边界速度处理
for i=1:d
for j=1:N
if v(j,i)>vlimit(i,2) %如果速度大于边界速度，则把速度拉回边界
v(j,i)=vlimit(i,2);
end
if v(j,i) < vlimit(i,1) %如果速度小于边界速度，则把速度拉回边界
v(j,i)=vlimit(i,1);
end
end
end
x = floor(x + v); % 位置更新
for j=1:N
if x(j,1)> plimit(2)
x(j,1)=plimit(2);
end
if x(j,1) < plimit(1)
x(j,1)=plimit(1);
end
if x(j,2)> plimit(2)
x(j,2)=plimit(2);
end
if x(j,2) < x(j,1)
x(j,2)=x(j,1);
end
end
record(iter) = fym; %记录最大值
iter = iter+1;
end
在满足预设的更新代数后，利用下边的代码输出结果，在这里还可以提供另一种迭代停止的思路，即最优值连续数代变化小于某个值时使得迭代停止。
%% 作图
figure(3);
plot(record); %画出最大值的变化过程
title('收敛过程')
threshold1 = ym(1);
threshold2 = ym(2);
[height,length]=size(Image_OSTU);
for i=1:length
for j=1:height
if Image_OSTU(j,i)>=threshold2
Image_OSTU(j,i)=255;
elseif Image_OSTU(j,i)<=threshold1
Image_OSTU(j,i)=0;
else
Image_OSTU(j,i)=(threshold1+threshold2)/2;
end
end
end
figure(4);
imshow(Image_OSTU);
xlabel(['最大类间差法阈值',num2str(ym)]);
在上述代码中，计算适应度的函数被封装如下：
%% 适应度函数
function fx = f(x)
Imag = imread('24063.jpg');%296059
Imag=rgb2gray(Imag);
[height,length]=size(Imag);
totalNum=height*length;
pixelCount=zeros(1,256);%统计各个像素值的个数
for i=1:length
for j=1:height
number=Imag(j,i)+1;
pixelCount(number)=pixelCount(number)+1;
end
end
pi=pixelCount/totalNum; %pi 灰度级为i的像素出现的概率
a=1:256;
fx = zeros(1, 500);
for i=1:500
m=x(i,1);
n=x(i,2);
w0=sum(pi(1:m));
w1=sum(pi(m+1:n));
w2=sum(pi(n+1:256));
mean0=sum(pi(1:m).*a(1:m))/w0;
mean1=sum(pi(m+1:n).*a(m+1:n))/w1;
mean2=sum(pi(n+1:256).*a(n+1:256))/w2;
fx(i)=w0*w1*(mean0-mean1)^2+w0*w2*(mean0-mean2)^2+w1*w2*(mean1-mean2)^2;
end
end
1.3 结果展示
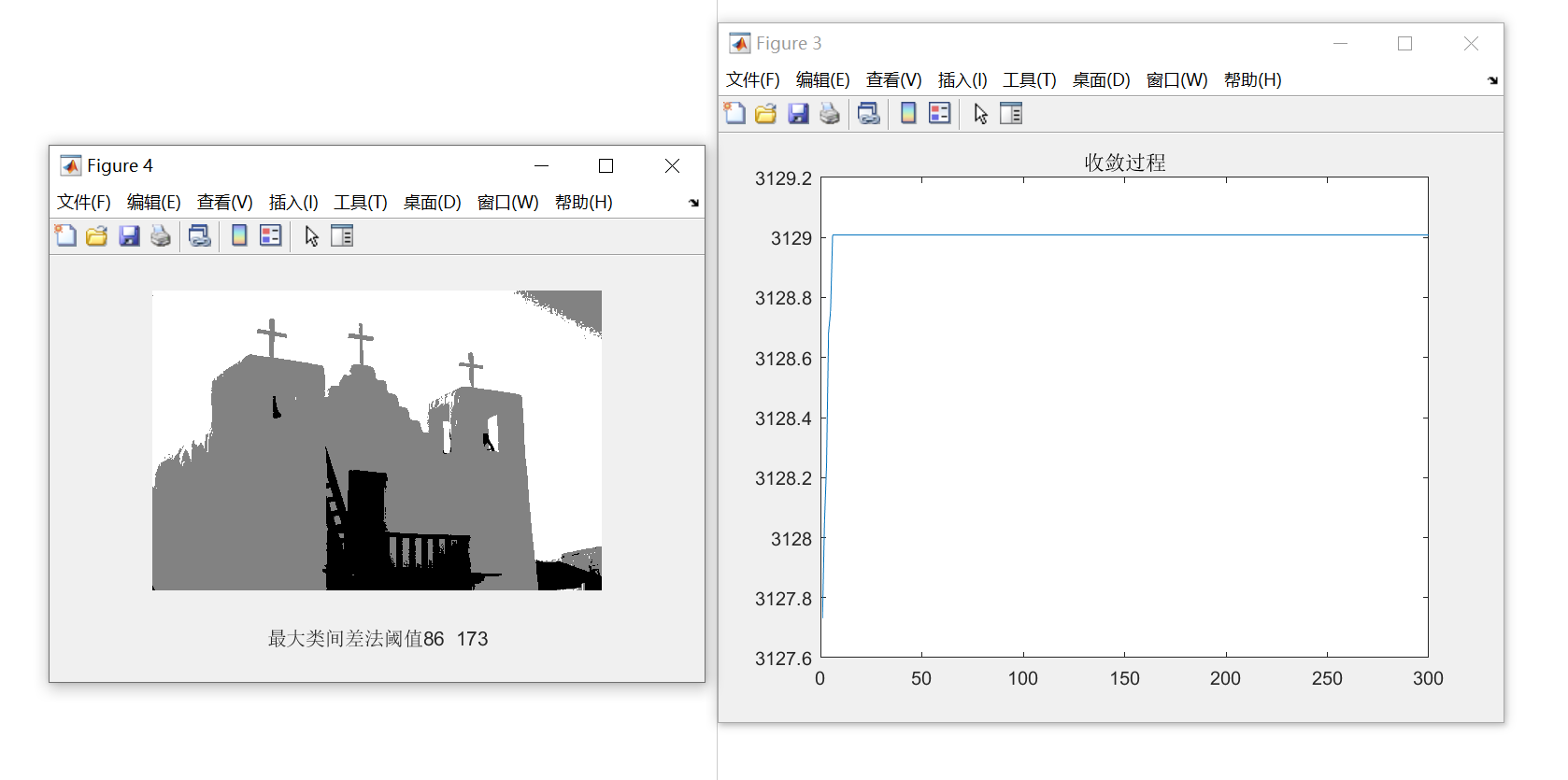
输入的图片如下图所示：
从结果中可多看出，函数迅速收敛，并且分割的效果还是不错的，将天空、白色墙壁与深色的门与楼梯较好的分离开来。
2. 利用遗传算法优化最大类间差双阈值分割
2.1 概述
遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。从遗传算法的运算过程可以看出：可行解的编码方法、遗传算子的设计是构造遗传算法时需要考虑的两个主要问题，也是设计遗传算法的两个关键步骤。对不同的优化问题需要使用不同的编码方法和不同操作的算子。
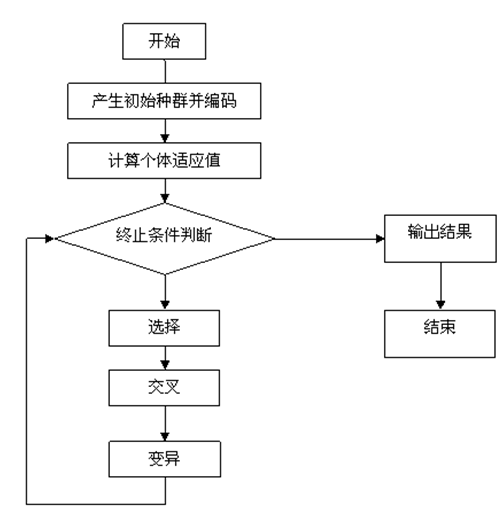
下面结合代码来看一下优化过程：
2.2 代码部分
输入要处理的图片，并对种群进行基本的定义，同时定义遗传算法的迭代过程。
%% 输入图像；
Imag = imread('24063.jpg');%296059
Imag=rgb2gray(Imag);
Image_OSTU=Imag;
%种群大小
popsize=100;
%二进制编码长度
chromlength=8;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群
pop = initpop(popsize,chromlength);
ger = 5000; % 最大迭代次数
iter=1; %初始的迭代次数因为用while设置为一
record = zeros(ger, 1); %记录器
while iter <= ger
%计算适应度值（函数值）
objvalue = cal_objvalue(pop);
fitvalue = objvalue;
%选择操作
newpop = selection(pop,fitvalue);
%交叉操作
newpop = crossover(newpop,pc);
%变异操作
newpop = mutation(newpop,pm);
%更新种群
pop = newpop;
%寻找最优解
[bestindividual,bestfit] = best(pop,fitvalue);
record(iter) = bestfit; %记录最大值
iter = iter+1;
end
下面对遗传算法的各个算子与适应度函数进行简单的介绍与代码展示：
首先初始化种群，并且定义二进制到十进制的转化函数binary2decimal（）。
%% 初始化种群
function pop=initpop(popsize,chromlength)
pop = round(rand(popsize,chromlength,2));
[px,py,pz]=size(pop); %px是矩阵的行，py是矩阵的列数，这里px是种群个数，py为染色体长度
%[r,c]=size(A),当有两个输出参数时，size函数将矩阵的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c。
for i = 1:px
for j = 1:py
if pop(i,j,1) == 0 && pop(i,j,2) == 1
continue
end
if pop(i,j,1) == 1 && pop(i,j,2) == 0
pop(i,j,2) = 1;
end
end
end
end
function pop2 = binary2decimal(pop)
[px,py,pz]=size(pop); %px是矩阵的行，py是矩阵的列数，这里px是种群个数，py为染色体长度
%[r,c]=size(A),当有两个输出参数时，size函数将矩阵的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c。
for j = 1:pz
for i = 1:py
pop1(:,i,j) = 2.^(py-i).*pop(:,i,j); %冒号代表对所有行都有这样的操作
%py-i相当于说第一列到最后一列的顺序倒置过来
end
end
%sum(.,2)对行求和，得到列向量
temp = sum(pop1,2);
pop2 = temp;
%根据X的取值范围进行2进制到10进制的转换，（ub-lb）相当于一个线段，temp/1023相当于二进制在这个区间上的占比，得到的结果再乘以（ub-lb）得到其在这段线段上的位置，再加上下界，就转换成了这个区间上的十进制。
end
然后是计算适应度函数
%% 计算适应度函数
function objvalue = cal_objvalue(pop)
Imag = imread('68077.jpg');%296059
Imag=rgb2gray(Imag);
[height,length]=size(Imag);
totalNum=height*length;
pixelCount=zeros(1,256);%统计各个像素值的个数
for i=1:length
for j=1:height
number=Imag(j,i)+1;
pixelCount(number)=pixelCount(number)+1;
end
end
pi=pixelCount/totalNum; %pi 灰度级为i的像素出现的概率
a=1:256;
objvalue = zeros(1, 100);
for i=1:100
m=binary2decimal(pop(i,:,1));%转化二进制数为x变量的变化域范围的数值
n=binary2decimal(pop(i,:,2));
w0=sum(pi(1:m));
w1=sum(pi(m+1:n));
w2=sum(pi(n+1:256));
if w0 > 0 && w1 > 0 && w2 > 0
mean0=sum(pi(1:m).*a(1:m))/w0;
mean1=sum(pi(m+1:n).*a(m+1:n))/w1;
mean2=sum(pi(n+1:256).*a(n+1:256))/w2;
objvalue(i)=w0*w1*(mean0-mean1)^2+w0*w2*(mean0-mean2)^2+w1*w2*(mean1-mean2)^2;
end
end
end
然后采用轮盘赌的形式对个体进行选择
%如何选择新的个体
%输入变量：pop二进制种群，fitvalue：适应度值
%输出变量：newpop选择以后的二进制种群
function [newpop] = selection(pop,fitvalue)
%构造轮盘
[px,py,pz] = size(pop);
totalfit = sum(fitvalue);%总的适应度值
p_fitvalue = fitvalue/totalfit;%每个适应度值在轮盘中的占比，也就是相对适应度的大小，即为每个个体被遗传到下一代群体中的概率
p_fitvalue = cumsum(p_fitvalue);%概率求和排序 cumsum()得到输入矩阵的每个元素对应的列向上（行向左）求和矩阵
ms = sort(rand(px,1));%从小到大排列 生成种群大小的0-1的随机数字，依据该随机数出现在上述哪一个概率区域内来确定各个个体被选
%中的次数
fitin = 1;
newin = 1;%行选择标量
%选出新的种群
while newin<=px %初始行向量为1，,从第一行开始遍历
if(ms(newin))<p_fitvalue(fitin)%当产生的随机数字<个体被遗传到下一代群体中的概率时，即为可遗传
newpop(newin,:,:)=pop(fitin,:,:);%遗传给新的种群
newin = newin+1;%遍历下一行
else
fitin=fitin+1;%如果不可遗传，就检查下一个更大的区域
end
end
end
交叉算子
%% 交叉
function [newpop] = crossover(pop,pc)
[px,py,pz] = size(pop);
newpop = ones(size(pop));
for z = 1:pz
for i = 1:2:px-1 %for循环的范围在1到px-1，步长为2，也就是从第一行到第三行到第五行一直到第px-1行
if(rand<pc)%当随机数小于交叉概率时才进行交叉
%rand没有参数的时候就是从均匀分布中生成一个0-1之间的随机数
cpoint = round(rand*py);%round是一个四舍五入的函数 用随机数*列数是在随机设置交叉点的位置
newpop(i,:,z) = [pop(i,1:cpoint,z),pop(i+1,cpoint+1:py,z)];%截取第i行交叉点前面的和第i+1行交叉点后面的进行连接
newpop(i+1,:,z) = [pop(i+1,1:cpoint,z),pop(i,cpoint+1:py,z)];%截取第i+1行交叉点前面的和第i行交叉点后面的进行连接
else %如果随机数大于交叉概率，也就是不进行交叉直接把pop中的种群数赋给交叉后的种群数
newpop(i,:,z) = pop(i,:,z);
newpop(i+1,:,z) = pop(i+1,:,z);
end
end
end
end
变异算子
%% 变异
function [newpop] = mutation(pop,pm)
[px,py,pz] = size(pop);
newpop = ones(size(pop));
for z = 1:pz
for i = 1:px %循环从第一行到最后一行
if(rand<pm) %如果随机数小于变异概率就发生变异
mpoint = round(rand*py); %随即产生变异点的位置
if mpoint <= 0
mpoint = 1;
end
newpop(i,:) = pop(i,:);
if newpop(i,mpoint,z) == 0
newpop(i,mpoint,z) = 1;
else
newpop(i,mpoint,z) = 0;
%对第i行变异点取反
end
else
newpop(i,:,z) = pop(i,:,z);
end
end
end
end
利用下边的函数求取当前种群最佳个体与最优适应度值
%% 种群最优
function [bestindividual, bestfit] = best(pop,fitvalue)
[px,py,pz] = size(pop); %获取矩阵的行数和列数，size（）将矩阵的行数给px，列数给py
bestindividual = pop(1,:,:);%把第一行的所有列弹出 赋给bestindividual，pop() 函数用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值。
bestfit = fitvalue(1); %这两行相当于在初始化最佳个体和最佳适应度值
for i = 2:px %for循环从第二行开始，
if fitvalue(i)>bestfit %如果改行的适应值大于最佳适应值，
bestindividual = pop(i,:,:);%把该行作为最佳个体，
bestfit = fitvalue(i);%该行适应值为最佳适应值
end
end
end
最后将结果输出：
%% 作图
figure(3);
plot(record); %画出最大值的变化过程
title('收敛过程')
threshold1 = binary2decimal(bestindividual(:,:,1));
threshold2 = binary2decimal(bestindividual(:,:,2));
[height,length]=size(Image_OSTU);
for i=1:length
for j=1:height
if Image_OSTU(j,i)>=threshold2
Image_OSTU(j,i)=255;
elseif Image_OSTU(j,i)<=threshold1
Image_OSTU(j,i)=0;
else
Image_OSTU(j,i)=125;
end
end
end
ym = zeros(1, 2); % 种群的历史最佳位置，两个维度，设置为0
ym(1) = threshold1;
ym(2) = threshold2;
figure(4);
imshow(Image_OSTU);
xlabel(['最大类间差法阈值',num2str(ym)]);
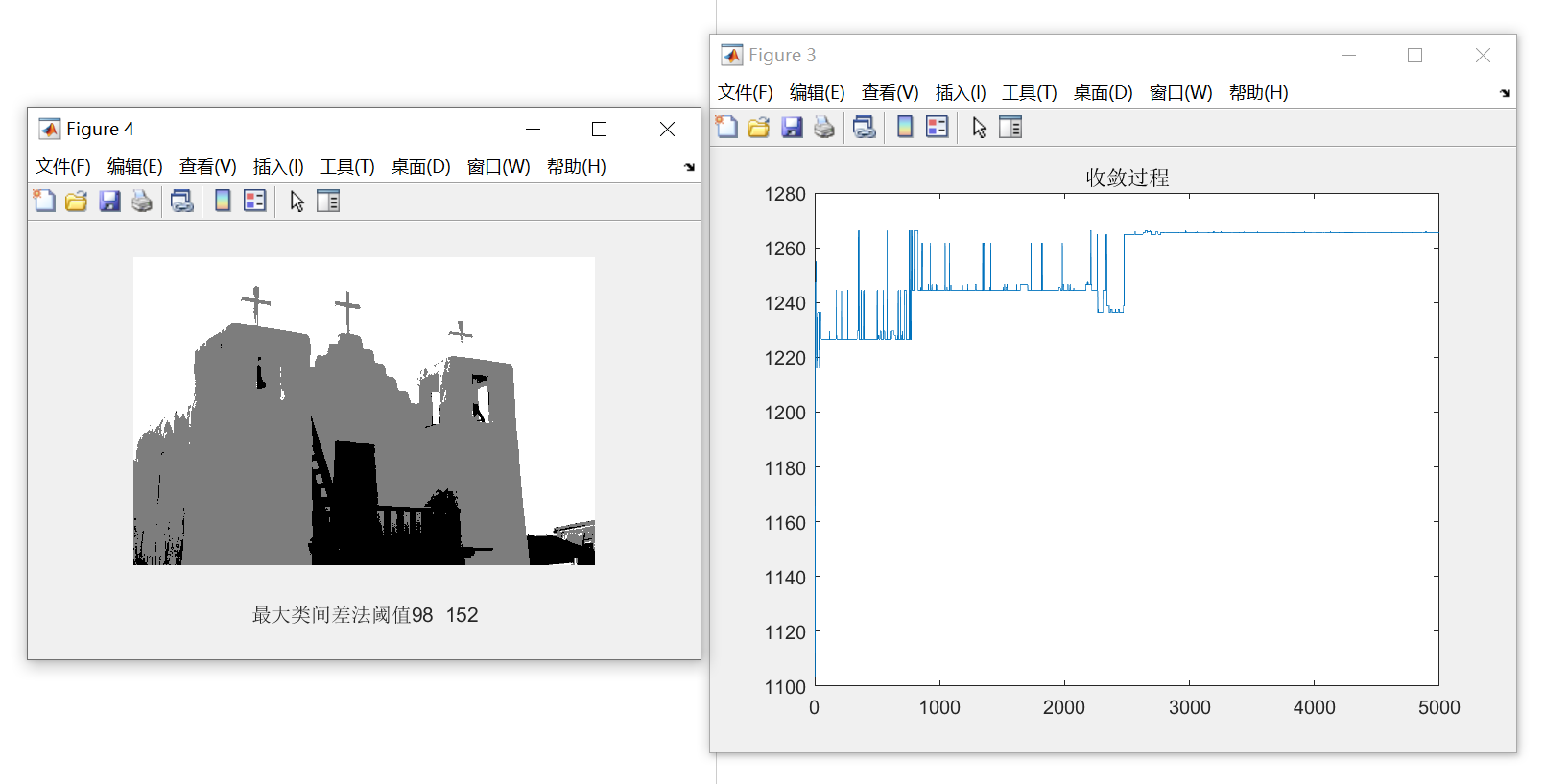
1.3 结果展示
输入的图片如下图所示：
从结果中可多看出，函数收敛速度不如粒子群算法，通过多次运行，分割效果也较不稳定，此案例更适合于利用粒子群算法进行优化。
三、总结
在图像的多阈值分割中，自我感觉粒子算法要优于遗传算法，大家可以根据自己的需要对算法的创新进行进一步的研究，包括遗传算法收敛速度较慢，粒子群算法更容易陷入局部最优解等问题。最后还上传了代码资源（链接为利用粒子群算法与遗传算法实现图像的自适应多阈值的快速分割.zip），可以根据情况下载。资源主要包括两部分：
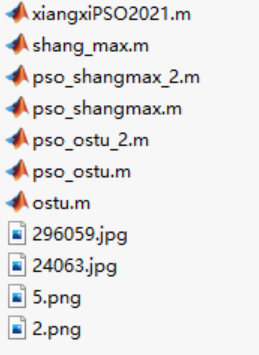
第一张图片从上至下依次为：粒子群算法示例，单阈值最大熵法，粒子群优化三阈值分割最大熵法，粒子群优化双阈值分割最大熵法，粒子群优化三阈值分割最大类间差法，粒子群优化双阈值分割最大类间差法，单阈值最大类间差法，还有几张图片…
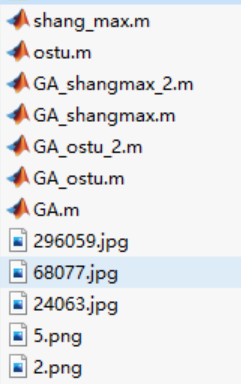
第二张图片从上至下依次为：单阈值最大熵法，单阈值最大类间差法，遗传算法优化三阈值分割最大熵法，遗传算法优化双阈值分割最大熵法，遗传算法优化三阈值分割最大类间差法，遗传算法优化双阈值分割最大类间差法，遗传算法示例，还有几张图片…
最后
以上就是欣喜路灯为你收集整理的【图像分割】利用粒子群算法与遗传算法实现图像的自适应多阈值的快速分割前言一、自适应多阈值分割二、代码部分（以粒子群算法与遗传算法优化自适应双阈值分割为例）三、总结的全部内容，希望文章能够帮你解决【图像分割】利用粒子群算法与遗传算法实现图像的自适应多阈值的快速分割前言一、自适应多阈值分割二、代码部分（以粒子群算法与遗传算法优化自适应双阈值分割为例）三、总结所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复