pytorch利用梯度下降求方程的最小值_day2

pytorch

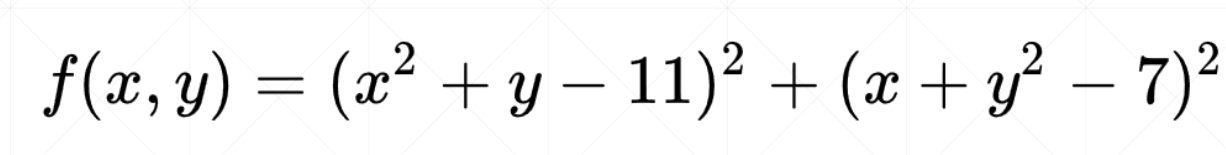
我们需要求解上面函数f（x,y）的最小值，方法如下。

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import torch


def himmelblau(x):  # 利用梯度下降计算这个函数的最小值
    return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2

#  这里是画函数图


x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X, Y = np.meshgrid(x, y)
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y])

fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()


# 下面是梯度下降的具体过程
x = torch.tensor([-4., 0.], requires_grad=True)  # 这里x表示的就是自变量x，y。[]里面是初始化的值，需要对x,y求导
optimizer = torch.optim.Adam([x], lr=1e-3)  # 使用Adam编译器，对自变量使用，学习速率：lr=1e-3
for step in range(20000):  # 迭代20000次

    pred = himmelblau(x)  # 预测的值是pred，要使pred达到最小

    optimizer.zero_grad()  # 首先将所有梯度清零
    pred.backward()  # 对pred反向传播，求得x，y每次的梯度
    optimizer.step()  # 这是代表更新一步，在这里面完成了自动利用梯度更新权值。这里是更新x,y

    if step % 2000 == 0:
        print('step {}: x = {}, f(x) = {}'.format(step, x.tolist(), pred.item()))

最后

以上就是奋斗飞鸟为你收集整理的pytorch利用梯度下降求方程的最小值_day2的全部内容，希望文章能够帮你解决pytorch利用梯度下降求方程的最小值_day2所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。