概述
本节介绍特征多项式和特征值与特征向量的计算
1 特征多项式
nxn矩阵A的特征多项式：
det(A - aI) 记做pa
2 求特征值与特征向量
对于方程det(A - aI) = 0 方程的根就是A的特征值，最后将特征值带入公式(A-aI)h=0中解出特征向量。
下边是两个例子：
(i) 例一
该方程有两个根：
他们就是特征值 带入求得对应的特征向量：
(ii)例二 利用特征值和特征向量求斐波那契公式的通项公式：
斐波那契数列的递推式：
数列的前10项：
0,1,1,2,3,5,8,13,21,34
用矩阵和向量重写递推式：
通过递推得到：
列出特征多项式的方程：
求解特征值如下：
对应的特征向量满足：
令特征向量第一个分量为1得：
将初始向量表示为特征向量的线性组合：
带入上边的递推式有：
由于数列都为整数:
最后
以上就是贤惠冬日为你收集整理的线性代数(二十九) ：特征值与特征向量的计算的全部内容，希望文章能够帮你解决线性代数(二十九) ：特征值与特征向量的计算所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
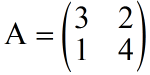
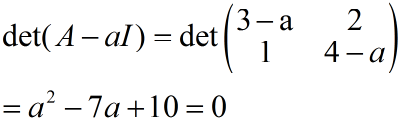
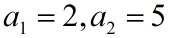
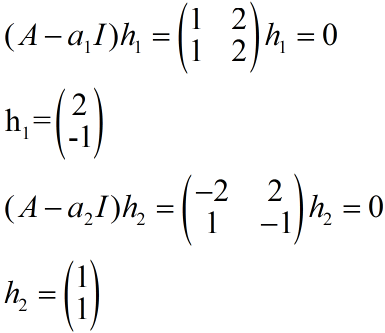
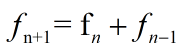
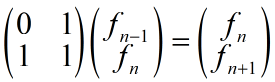
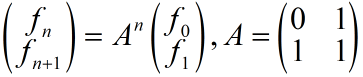
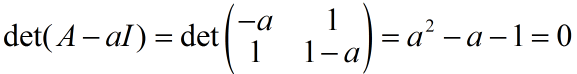
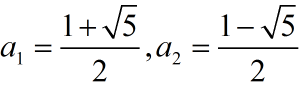
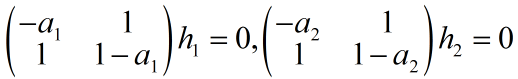
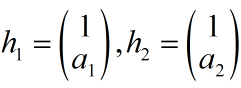
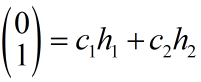
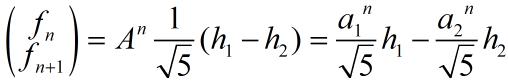
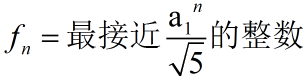
发表评论 取消回复