LeetCode137——只出现一次的数字II

78 阅读 0 评论 52 点赞

我是靠谱客的博主孝顺水壶，最近开发中收集的这篇文章主要介绍LeetCode137——只出现一次的数字II，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

我的LeetCode代码仓：https://github.com/617076674/LeetCode

原题链接：https://leetcode-cn.com/problems/single-number-ii/description/

题目描述：

知识点：位运算

思路：位运算

本题是LeetCode136——只出现一次的数字的加强版，下述解法讨论均参考于Detailed explanation and generalization of the bitwise operation method for single numbers。

（1）问题的一般化：

给定一个非空整数数组，除了某个元素只出现p次以外，其余每个元素均出现了k（k > 1）次。找出那个只出现了p（p >= 1且p % k != 0）次的元素。

（2）考虑数组中的元素不是0就是1的情况，即1位的情况

整数在计算机中是按位存储的，一个int型的整数在计算机中是按32位存储的。我们先考虑数组中的元素不是0就是1的情况，即1位的情况。现在，我们需要统计数组中1的数量，我们的统计规则是：当1的数量达到k时，从0开始重新计数，即1的数量为k时，相当于1的数量为0，而1的数量为k + 1时，相当于1的数量为1。我们用一个m位的二进制数：xm, ..., x1来对1的数量进行计数。

从上述分析中，我们可以得出以下4点结论：

a：计数器的初始值是0，即xi = 0(i = 1, ..., m)。

b：遍历数组中的每一个元素，一旦遇到0，我们的计数器保持不变。

c：遍历数组中的每一个元素，一旦遇到1，我们的计数器需要加1。

d：对于一个m位的二进制数，其能计数到的最大值是2 ^ m - 1，而我们现在的计数最大值需要能够达到k - 1，因此需要满足条件2 ^ m >= k。

现在的关键问题在于：当我们遍历数组时，我们采取什么样的位操作使得xm, ..., x1的值发生变化呢？

考虑上述结论b，我们可以使用x = x | 0或x = x ^ 0这两种操作来使得我们的计数器在遇到0时保持不变，我们究竟应该选择哪种操作呢？

对实际过程进行模拟，从初始时刻开始，初始时xi = 0(i = 1, ..., m)。由于我们之前已经考虑了结论b，我们来考虑结论c。在遍历数组中的元素时，一旦我们遇到了第一个1，我们需要改变计数器的状态为：xm = 0, ..., x2 = 0, x1 = 1。当我们遇到第二个1时，我们需要改变计数器的状态为：xm = 0, ..., x2 = 1, x1 = 0。对于x1 = x1 | nums[i]操作，在遇到第二个1时，显然无法将x1从1变为0，而x1 = x1 ^ nums[i]却可以。因此，我们选择的位操作是x1 = x1 ^ nums[i]。

现在，我们的问题变成了：xm, ..., x2, x1状态发生改变的条件是什么？

对于x1，其发生改变的条件是：遍历数组时，遇到1。

对于x2，其发生改变的条件是：遍历数组时，遇到1，且x1 = 1。因为如果此时x1 = 0，那么我们只需令x1 = 1就可以达到计数器加1的目的，无需改变其他位的值。

同理，对于xm，其发生改变的条件是，遍历数组时，遇到1，且xm - 1, ..., x1均为1。

现在，我们还存在的问题是：对于m位的二进制数xm, ..., x1，其计数归0的值是2 ^ m，而不是k。如何使得计数器在达到k时归0？

我们需要设置一个变量mask，当计数器的值到达k时，mask = 0，其余时刻mask = 1。这样定义之后，我们只需要令xm = xm & mask, ..., x1 = x1 & mask就可以实现计数器在达到k时归0的目的。

那么，我们的问题就变成了：如何计算mask的值，使得其满足上述定义呢？

对于数字k，我们将其表示成二进制形式km, ..., k1。当我们的计数达到k时，显然有xi = ki(i = 1, ..., m)。因此，mask = ~(y1 & y2 & ...& ym)，如果kj = 1，那么yj = xj；如果kj = 0，那么yj = ~xj(j = 1, ..., m)。

由上述分析可知，我们的算法的伪码如下：

for (int i : nums) {
    xm ^= (xm-1 & ... & x1 & i);
    xm-1 ^= (xm-2 & ... & x1 & i);
    .....
    x1 ^= i;
    
    mask = ~(y1 & y2 & ... & ym) where yj = xj if kj = 1, and yj = ~xj if kj = 0 (j = 1 to m).

    xm &= mask;
    ......
    x1 &= mask;
}

（3）考虑数组中的元素是32位数的情况

现在，我们需要将数组中的元素是1位数的情况推广到32位数的情况。一个想法是对每一位都创建一个计数器，这样就总共有32个计数器。当然，利用位运算的性质，我们可以用m个32位的整数来替代32个m位计数器，理由很简单：按位运算仅适用于每个位，因此对不同位的操作彼此独立。示意图如下：

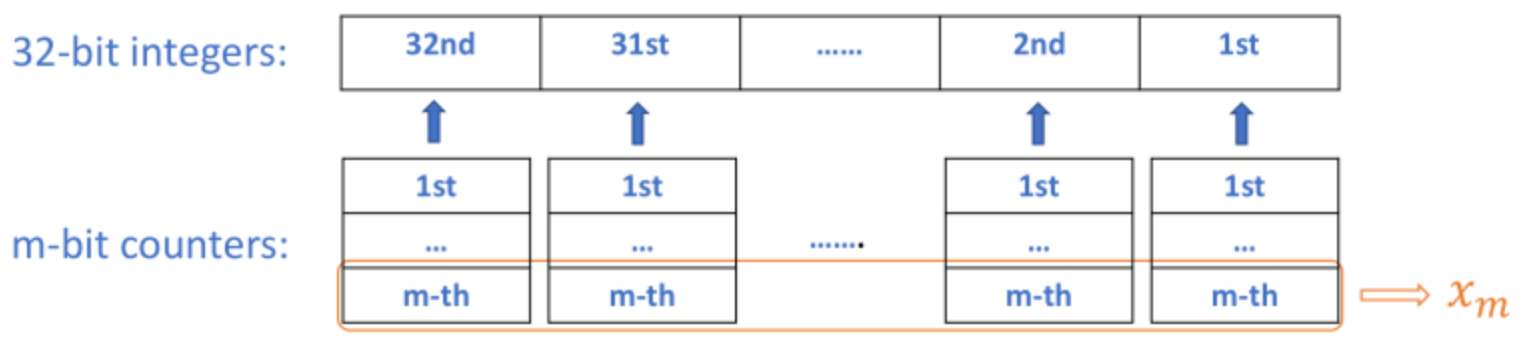
顶部的长方框代表一个32位的整数，每个位都对应一个m位的计数器（显示在相应方框的下面）。由于按位运算对不同位的操作是彼此独立的，我们可以把所有计数器的第m位组成一个32位的整数（如橙色方框所示）。在这个32位数中的所有位有着相同的位运算操作。由于每个计数器有m位，我们得到m个32位整数xm, ..., x1，但是现在这些都是32位的数，而不是（2）中的1位数，其余的算法部分和（2）中均相同。

（3）返回什么结果

最后，我们需要明确的一个问题是：在xm, ..., x1中，哪一个是我们寻找的那个数呢？即哪个是出现了p次的数呢？

为了回答这个问题，我们需要理解xm, ..., x1分别代表的含义。以x1为例，其有32位，我们将其标记为r（r = 1, ..., 32）。在我们扫描了整个数组之后，x1的第r位由数组中所有数字的第r位确定。更准确地说，假设数组中所有元素的第r位的1的数量为q，令q' = q % k，将q'表示成二进制形式：q'm, ..., q'1，根据定义，x1的第r位和q'1相等。

那么，现在我们的问题是：如果x1的第r位是1，这代表着什么呢？

回答这个问题的关键是，我们必须明确哪些值能对x1的第r位造成影响？

那些在数组中出现了k次的的数字显然不会对x1的第r位造成影响。对x1的第r位造成影响的元素必须满足两个条件：

a：该元素的第r位是1。

b：该元素在数组中的出现次数不是k的整数倍。

条件a是显而易见的。对于条件b，是因为当该元素的出现次数满k次时会归0。因此，只有那个出现了p（p % k != 0）次的元素会对x1的第r位造成影响。如果p > k，那么前面的k * [p / k]（[p / k]代表p / k的整数部分）个元素不会对x1的第r位造成影响。因此，我们需要令p' = p % k，且该元素出现的有效次数其实是p'次。

将p'写成二进制形式：p'm, ..., p'1（由于p' < k，所有其可以填充进m位二进制数里）。我们先抛出一个结论：

xj和那个出现了p次的元素相等的条件是p'j = 1（j = 1, ..., m），下面给出证明。

如果xj的第r位是1，证明那个出现了p次的元素的第r位也是1（否则，没有任何因素能使得xj的第r位是1）。我们只需要证明：如果xj的第r位是0，那么那个出现了p次的元素的第r位也一定是0。

当xj的第r位是0时，假设那个出现了p次的元素的第r位是1。在遍历完整个数组之后，这个1会被计数p'次。根据定义，xj的第r位和p'j相等，而p'j = 1，因此xj的第r位时1，这就产生了矛盾。因此，我们得出结论：当p'j = 1时，xj的第r位和那个出现了p次的元素的第r位相等。由于对r = 1, ..., 32的每一位都有上述结论，因此当p'j = 1时，有xj和那个出现了p次的元素相等。

所以我们可以返回任意一个xj，只要满足p'j = 1即可。

算法的时间复杂度是O(n * logk)，其中n为数组中的元素个数。空间复杂度是O(logk)。

注：

事实上有如下关系：(xj)_r = s_r & p'j，其中(xj)_r代表xj的第r位，s_r代表那个出现了p次的元素的第r位。

当p'j = 1时，(xj)_r = s_r。

当p'j = 0时，(xj)_r = 0。

因此我们得到：

当p'j = 1时，xj = s。

当p'j = 0时，xj = 0。

因此，我们最后也可以返回(x1 | x2 | ... | xm)。

对于本题而言，k = 3（二进制：11），p = 1（二进制：1）。因此我们只需取m = 2，用两个32位数字x2和x1作为计数器。由于2 ^ m = 4 > k，因此我们需要一个mask变量，其值取为~(x1 & x2)。由于p表示为二进制是1，因此我们直接返回x1即可。当然，我们也可以选择返回（x1 | x2）。

时间复杂度是O(n)。空间复杂度是O(1)。

JAVA代码：

public class Solution {
    public int singleNumber(int[] nums) {
        int x1 = 0, x2 = 0, mask = 0;
        for (int i = 0; i < nums.length; i++) {
            x2 ^= x1 & nums[i];
            x1 ^= nums[i];
            mask = ~(x1 & x2);
            x2 &= mask;
            x1 &= mask;
        }
        return x1;
    }
}

LeetCode解题报告：