富集分析的原理与实现

一般做完差异分析都会做这一步，目的是找到差异基因富集到的通路，进而与生物学意义联系起来。具体的统计方法很简单，这篇笔记里面的代码可以从零搭建一个富集分析工具。

后台回复20211007获取本文的测试数据和代码，以及（单细胞）转录组分析中可能用到的GO KEGG富集分析代码（这部分本文不演示）。

关于Gene Ontology (GO), KEGG这些背景就不讲了，网上很多资料。

将富集分析中的问题抽象出来，其实就是下图的“摸球”问题。

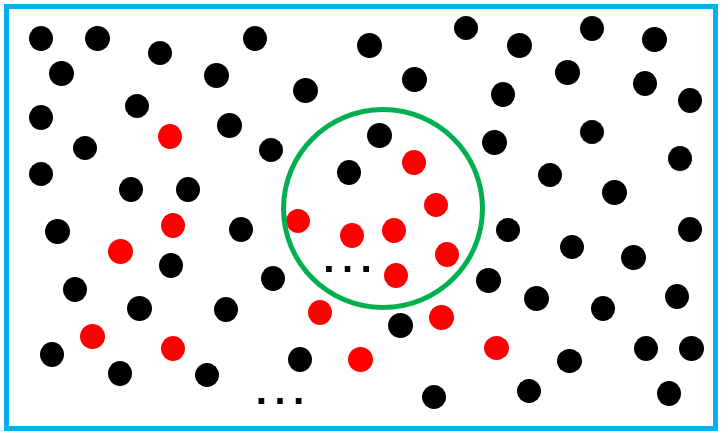
蓝色方框中的球是所有的基因【共N个】，在探究某个特定通路P时，通路里面涉及到的基因用红色表示【共M个】。绿色圆圈是一次摸球事件，用来表示做了一次差异分析得到的基因【共n个】，这些基因中，有属于通路P的(红色球)【共k个】，有不属于的(黑色球)。

用摸球问题中的语言再描述一次：袋子中共有黑球和红球N个，其中红球M个。某次抽样中，一共摸球n个，其中红球k个，问在这次摸球中，红球的占比是否显著高于袋子中红球的占比？
（以前学摸球问题/超几何分布的时候，可能只求概率，没有进一步到这个统计检验）

回答这个问题，需要求出问题中这个事件的概率以及更极端事件的概率之和，也就是p值，小于0.05或者0.01就能认为是显著了。

1. 一个通路，计算p值

接下来以一个GO term (GO_extracellular_matrix_organization)为例，计算p值。
用的通路基因集是小鼠 GO BP的基因集，差异基因集是单细胞转录组分析中一个cluster的高表达基因

library(tidyverse)
library(clusterProfiler)

gmt.df=read.gmt("Mm.c5.bp.v7.1.SYMBOL.gmt")
deg=read.table("test_deg.txt",header = T,sep = "t",stringsAsFactors = F)
deg=deg[deg$gene %in% gmt.df$gene,]

这种情况下，前面说的几个参数的值如下：

• 全部球的个数/全部基因数：
  N=length(unique(gmt.df$gene))
• 全部红球的个数/通路基因集的基因数：
  one.set=gmt.df[ gmt.df$term %in% c("GO_extracellular_matrix_organization") ,] M=length(one.set$gene)
• 摸球数/差异基因数：
  n=length(deg$gene)
• 摸球中红球的个数/差异基因中属于这个通路的基因数：
  k=sum(deg$gene %in% one.set$gene)

N M n k的值分别为: 23210, 271, 47, 6

求p值之前，先看一下满足N M n这三个参数的超几何分布，在不同的k值之下的概率：

df1=data.frame(x=1:47,y=dhyper(x=1:47, M, N-M, n))
df1%>%ggplot(aes(x,y))+geom_point()+
  geom_line()+
  geom_vline(xintercept=k,color="red",linetype=5)+  #这里k等于6，其作为阈值
  theme_bw()+
  theme(panel.grid = element_blank())

dhyper()用来求概率，四个参数分别是：摸球中红球个数的向量，袋中红球数，袋中黑球数，摸球数

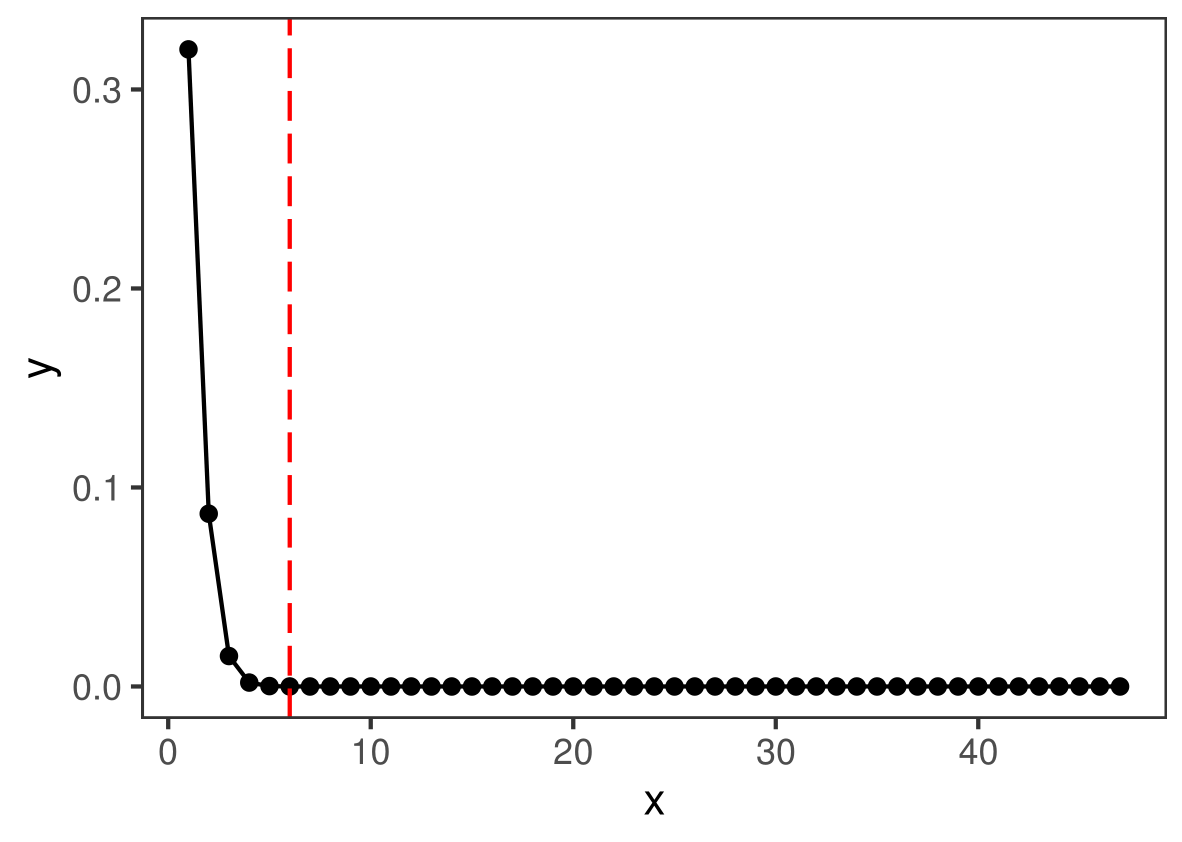
我们要计算的就是红线以及右边那些红球数对应的概率之和，如下：

> phyper(k-1,M, N-M, n, lower.tail=FALSE)
[1] 1.722659e-05

当lower.tail=FALSE，计算的是P[X > x]，即大于第一个参数的概率之和。上面的代码第一个参数写的是k-1，因为我们需要求k以及k右边的概率之和。

以上是对一个通路求p值

2. 多个通路，依次计算p值

如果是多个通路，需要循环操作，依次对每个通路进行富集分析。
下面的演示用到的差异基因集和GO BP基因集同上

分析哪些pathway？要满足两个条件：

• 通路里面基因的数量满足一定要求
• 至少和deg有基因交集

下面的代码就是对通路做过滤的

bp.stat=as.data.frame(table(gmt.df$term))
colnames(bp.stat)[1]="pathway"
bp.stat=bp.stat%>%filter(Freq >= 2 & Freq <= 2000)

tmp.df=gmt.df
tmp.df$TF=tmp.df$gene %in% deg$gene
tmp.stat=as.data.frame(tmp.df %>% dplyr::group_by(term) %>% dplyr::summarize(counts=sum(TF)))
tmp.stat=tmp.stat%>%filter(counts > 0)
keep.pw=sort(intersect(bp.stat$pathway,tmp.stat$term))

下面就是循环求p值了

N=length(unique(gmt.df$gene))
n=length(deg$gene)
term=c()
pvalue=c()

for (i in keep.pw) {
  one.set=gmt.df[ gmt.df$term %in% i ,]
  M=length(one.set$gene)
  k=sum(deg$gene %in% one.set$gene)
  one.pvalue=phyper(k-1,M, N-M, n, lower.tail=FALSE)
  term=append(term,i)
  pvalue=append(pvalue,one.pvalue)
}

my_go_res=data.frame(term=term,pvalue=pvalue)
my_go_res=my_go_res%>%arrange(pvalue)

到这会儿还没有结束，还差一个FDR

3. 计算矫正p值

FDR, False Discovery Rates。为什么要控制FDR，降低假阳性。
这里用到的是The Benjamini-Hochberg method

The Benjamini-Hochberg method

假设我们对10个通路做了富集分析，我们会先得到10个p值：

1. 将这10个p值从小到大排序
2. 从1到10给这些p值排序
3. 最大的FDR adjusted p value（第10位）等于原来最大的那个p值
4. 第9位的FDR adjusted p value等于这两个值中的较小值：
   ①前一位矫正的p值；
   ②当前未矫正的p值 * （p值总个数/当前位数）
5. 重复第4步，直到第1位

代码如下：

fdr=c()
for (i in dim(my_go_res)[1]:1) {
  if (i==dim(my_go_res)[1]) {
    tmpfdr=my_go_res$pvalue[i]
  }else{
    tmpfdr=min(tmpfdr,my_go_res$pvalue[i] * (dim(my_go_res)[1] / i))
  }
  fdr=append(fdr,tmpfdr)
}
my_go_res$p.adj=rev(fdr)

到这儿富集分析的完整流程才算结束

4. 轮子有现成的

当然，这个算法已经非常常见了，clusterProfiler的enricher()就能够自定义基因集做富集分析。使用如下：

deg_gmt=clusterProfiler::enricher(deg$gene,TERM2GENE = gmt.df,minGSSize = 2,maxGSSize = 2000)
go_res=deg_gmt@result

和上面的结果是一模一样的。

今天的内容就到这里，后台回复20211007获取本文的测试数据和代码，以及（单细胞）转录组分析中可能用到的GO KEGG富集分析代码（这部分本文不演示）

最后

以上就是炙热冬天为你收集整理的富集分析的原理与实现的全部内容，希望文章能够帮你解决富集分析的原理与实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。