剑指Offer---------顺时针打印矩阵

63 阅读 0 评论 42 点赞

我是靠谱客的博主耍酷汉堡，最近开发中收集的这篇文章主要介绍剑指Offer---------顺时针打印矩阵，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目：输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10。

顺时针打印二维矩阵，如下图所示：

这是一个6X6的矩阵，每一个小方格我们都可以看做是一个数值（矩阵的元素）。

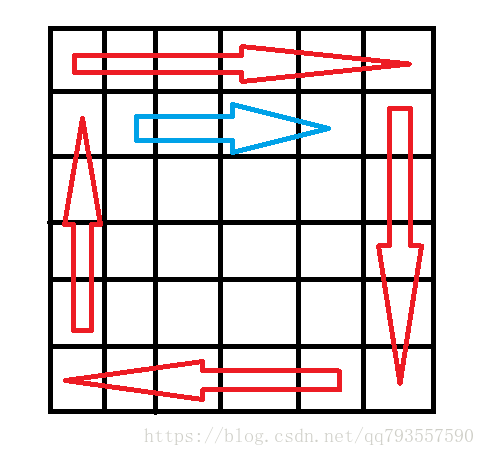
从上图我们可以发现，顺时针访问矩阵这个过程是从矩阵的外到内，一圈一圈地访问过去，直至访问完全部数值。然而这个过程是无法使用任何高效算法或者利用某个数据结构可以简单解决。我们可以做的是如何能够简单易解地去解决这个问题。

下面开始解决这个问题

从下图可以看到，每一圈的起点，都是处于对角线上的方格。如果使用坐标来表示，第一圈的起点是（0,0）、第二圈则从（1,1）开始，最后一圈的起点就是（2,2）。

整个过程如下图所示：

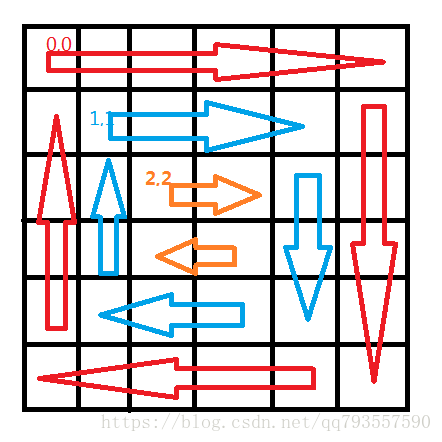
按照这条思路：

我们就可以使用循环来表示这个过程了。

public ArrayList<Integer> printMatrix(int [][] matrix) {
      if 矩阵为空
      return null;

    //一圈一圈地访问矩阵
    while(条件)
      //可以使用函数来访问
      printARount()
      
      //完成之后，开始下一圈的访问 
}

我们需要解决的就是循环条件和打印函数

什么时候是满足循环条件的呢？

例如：一个6X6的矩阵，最后一圈的起点是（2,2）

而一个7X7的矩阵，最后一圈的起点则是（3,3）

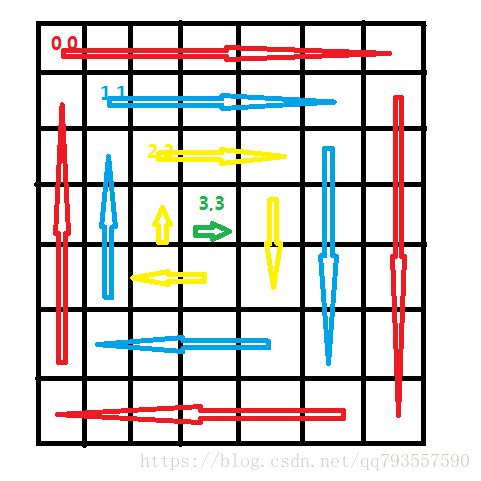
因为每一圈的起点都是沿（正）对角线的位置分布，沿反对角线对称。所以起点都不会过半，一直在上三角形部分

下图是7X7矩阵

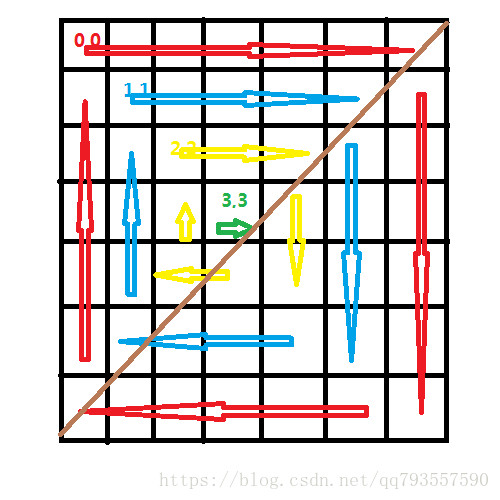
一个6X6的矩阵，行满足 6>2x2，列也满足 6>2x2

一个7X7的矩阵，行满足 7>3x2，列同理

PS：第一圈都是从（0,0）开始，乘以2的原因是反对角线对称，是处于上三角形。

public ArrayList<Integer> printMatrix(int [][] matrix) {
      if 矩阵为空
      return null;
    //获取矩阵的行数
    int rows = matrix.length;
    //获取矩阵的列数
    int columns = matrix[0].length;
    //从0开始
    int start = 0;
    //一圈一圈地访问矩阵
    while(rows > start*2 && columns > start*2)
      //可以使用函数来访问
      printARount()
      start ++;
      
      //完成之后，开始下一圈的访问 
}

接下来就剩下打印函数了

1、通常情况下，我们顺时针遍历矩阵包含四个步骤：从左到右、从上到下、从右到左、从下到上。

2、在特殊情况下，就不一定都会执行这四个步骤。

2.1、例如：当最后一圈是一行时（一个数也是一行），我们就只执行从左到右这一步

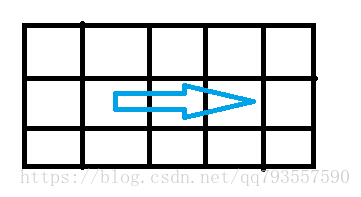
2.2、当最后一圈是一列的时候，我们会执行从左到右和从上到下两步

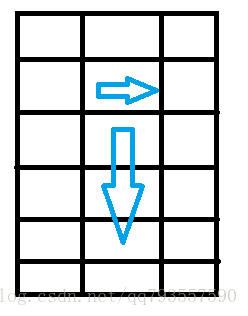
2.3、当最后一圈行数多于1行时并且多于2列的时候，就会执行从左到右、从上到下、从右到左这三步

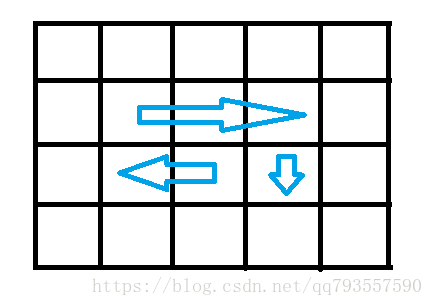
也就是说，如果多于2行并且多于2列的时候，我们就会执行从下到上这一步。

3、分析上面的情况，可以帮助我们得到执行四个步骤的前提条件

3.1、我们可以得出，第一步一定会执行

3.2、第二步，只有在行数多于一行的时候就会执行

3.3、第三步，只有在列数多于一行的时候回执行

3.4、第四步，只有在行数多于两行并且列数多于两列的时候就会执行

所以，打印函数：

public void addRecord(ArrayList<Integer> list,int start, int row , int column,int[][]matrix) {
		//获取该圈中，x(行)，y(列)的最终点
		int endX = row - 1 - start;
		int endY = column - 1 - start;
		
		//从左到右这一步一定会执行
		for(int i = start; i <= endY; i++) {
			list.add(matrix[start][i]);
		}
		//而从上到下，在多于1行时，就可以执行
		if(endX > start) {
			for(int i = start+1; i <= endX; i++) {
				list.add(matrix[i][endY]);
			}
		}
		//从右到左，只有在多于1行就会执行
		if(endX > start &&endY > start) {
			for(int i = endY - 1; i>=start; i--) {
				list.add(matrix[endX][i]);
			}
		}
		//而从下到上，只有在多于2行，并且多于1列的时候会执行
		if(endX > start+1 && endY > start) {
			for(int i = endX - 1; i>start;i--) {
				list.add(matrix[i][start]);
			}
		}
	}