算法：螺旋矩阵

59 阅读 0 评论 39 点赞

我是靠谱客的博主等待星月，最近开发中收集的这篇文章主要介绍算法：螺旋矩阵，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

算法描述

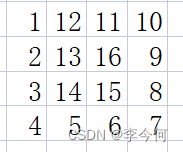
问题描述：打印一个矩阵，数值为依次从小到大螺旋式分布
图例如下

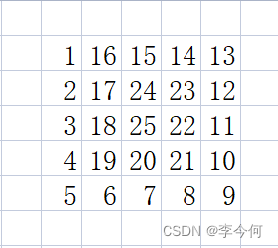
问题规模：1.规定矩阵大小为n*n(n为输入的一个数值，temp记录初始值n)

确定起始坐标（1,1）
确定起始值num

算法：1.利用递归法：Filling(n,num,begin,temp)从外层到内层

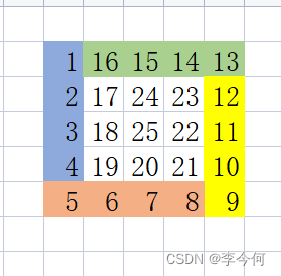
每一层划分为ABCD区
A区：
for i:begin totemp-1
matrix[i][begin] = num
num++

B区：
for i:begin to temp-1
matrix[temp][i] = num
num++

C区:
for i : temp totemp-n+1
matrix[i][temp] = num
num++

D区:
for i :temp to temp-n+1; i–)
matrix[begin][i] = num
num++
递归条件改变,进入下一层

n-=2;
begin++;
temp–;
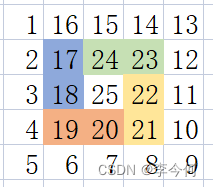
递归结束条件：n为奇数，if(n==1) matrix[begin][begin]=num;
begin++，return;

n为奇数
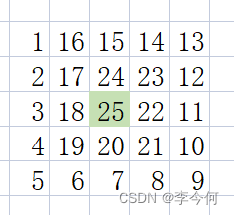
n为偶数，if(n==0)return

在这里插入图片描述

实验代码

import java.util.Scanner;
public class Main {
    static int[][] matrix =new int[100][100];
    public static void main(String[] args) {
        System.out.println("请输入矩阵的大小n:");
        Scanner in=new Scanner(System.in);
        int n=in.nextInt();
        int num=1;
        int begin=1;
        int temp=n;
        Filling(n,num,begin,temp);
        //打印出矩阵
       for(int k=1;k<=n;k++){
            for(int l=1;l<=n;l++){
                System.out.print(matrix[k][l]+"t");
            }
            System.out.println();
        }

    }
    public static void Filling(int n,int num,int begin,int temp) {
        if(n==1) {matrix[begin][begin]=num; begin++;return;}
        if(n==0)return;
            //A区域
            for (int i = begin; i <= temp-1 ; i++) {
                matrix[i][begin] = num;
                num++;
            }
            //B区域
            for (int i = begin; i <= temp-1 ; i++) {
                matrix[temp][i] = num;
                num++;
            }
            //C区域
            for (int i = temp ; i > temp-n+1; i--) {
                matrix[i][temp] = num;
                num++;
            }
            //D区域
            for (int i = temp ; i > temp-n+1; i--) {
                matrix[begin][i] = num;
                num++;
            }
            n-=2;
            begin++;
            temp--;
        Filling(n,num,begin,temp);
        }




}