哇,咱们公众号有100个小伙伴了,大家冲冲冲!

温馨提示
据说,李永乐复习全书每道题都滚瓜烂熟,可以有120的潜力。那么,我们一定要加油掌握每一道题呀。
学习目标:
掌握知识点
掌握解题方法
做题,做题,做题!
第一章:函数,连续,极限:
考点1:求极限
一、函数极限
比较基础,真题里面貌似没出过难题~
二、数列极限(标粗部分就是例题所用方法)
知识点一:n项和的数列极限常用方法(基本题)
(1)夹逼原理(2)定积分定义(3)级数求和
注:主体部分和变化部分相比同量级,采用定义分定义
主体部分和变化部分相比次量级,采用夹逼原理
题目:
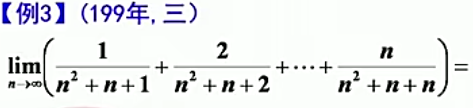
答案:

知识点二:类似2018年数列极限的题目,做个类比(难题)
题目:
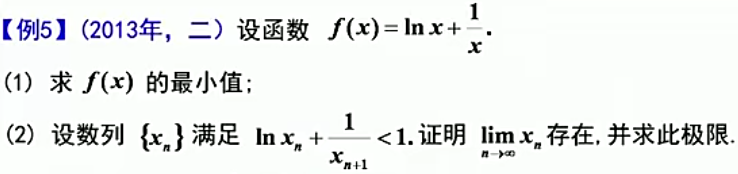
答案:

注意!一定要说明a是唯一的,不然就会扣分,参考2018年的那道数列极限
转送点,数学一18年真题
知识点三:(基本题)
(1)递推关系定义的数列极限常用的方法
1.单调有界证极限
2.单调有界不好证或者根本不单调,现在草稿纸上算结果,然后证明这个结果就是他的极限,这种题就是放缩了
(2)判断单调性的方法(一般方法)
1.相邻项相减
2.相邻项相除
3.通过结论:(归纳法可以证明,题目直接用)
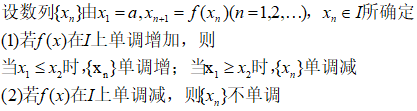
考点2:无穷小阶的比较(题目简单~)
考点3:连续性及间断点的类型(题目简单)
第二章 一元函数微分学:
考点1:导数定义(简单)
考点2:求导数(隐函数、参数方程、高阶导数)(简单)
考点3:函数性态(单调性、极值与最值,凹向与拐点)
知识点一:(基本题,但是往年做的情况很不好,数一数二考点)
曲率的公式要记住:
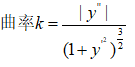
题目:

答案:

知识点二:(选择题里面比较难的了)
1.曲率圆是啥玩意儿?(口水话)
曲率圆的半径为曲率的倒数,在曲线某一点处的一阶导和二阶导,与对应曲率圆在该点的一阶导二阶导是相等的;从几何上看,曲率圆要在曲线凹的那一侧
2.曲率圆定义:
设在曲线M点,y''不为0.经过点M在曲线的凹向作该曲线的法线,在法线上取点C,以CM=1/k 为半径,C为圆心所作的圆周称为曲线在点M处的曲率圆,它的半径称为曲线在点M处的曲率半径。
曲线上点M出的曲率圆位于L的凹侧并且此曲率圆与曲线L在点M处的切线相切
题目:

答案1:(严格的去证明)

答案2:(数形结合的思想)

考点4:方程的根
知识点:(难题,实际上不算难,但是得分率很低)
方程根的问题,如果出现参数,把参数分离出来,一般会比较方便;同时这类题,往往需要画图(草稿纸上进行)
题目:

答案:

最后一步,判断f(x)单调减之后,草稿纸上做图判断:
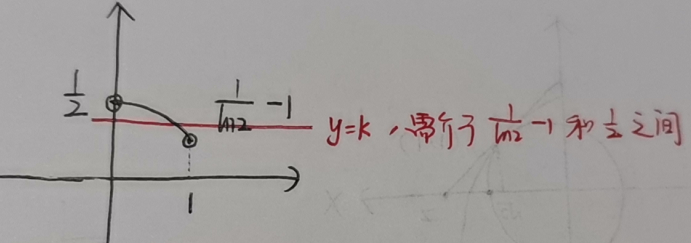
考点5:证明函数不等式
知识点:(难题)
通过单调性解决不等式问题的时候,适当的选取辅助函数是个难点
抽象来说,要灵活的选取,看看具体例子~
题目:
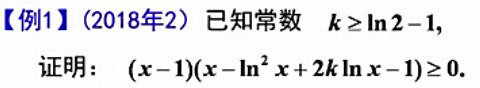
答案:

考点6:微分中值定理的证明题
知识点:(难题)
1.费马定理(可导条件下极值点的必要条件)
设f(x)在x=x0的某邻域U(x0)内有定义,f(x0)是f(x)的一个极值,又设f'(x0)存在,则f'(x0)=0
2.费马引理(解题关键)
设f(x)在x=x0的某邻域U(x0)内有定义,并在x0处可导,且f(x0)是f(x)的一个最值,则f'(x0)=0
3.面对高阶导选用泰勒展开的时候,具体在哪个点展开式难点;原则上是选取信息多的点
4.证f'(a)=0:(1)罗尔定理(2)费马引理
5.多项式法(第二问可以用)
构造一个多项式,要求的是几阶的导数,就构造几阶的多项式;
构造他干什么?我们要用他来进行罗尔定理;
具体用法看答案
题目:

答案:(第二问有两种解法)
解法一:

解法一可以看到,第二问说明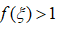 太牵强了,就带有凑的味道,实际上第一问用费马引理做,第二问泰勒展开的点才很容易想到在哪一点展开:
太牵强了,就带有凑的味道,实际上第一问用费马引理做,第二问泰勒展开的点才很容易想到在哪一点展开:

上面的第二问解法都很容易想到,就是泰勒选取展开点的问题
下面第二问还有解法,来自网友:线性代数超级难
第二问不用高阶泰勒展开用构造辅助函数(多项式法)的方法:
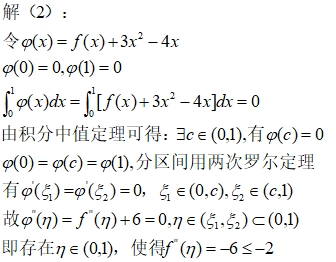
但是这个辅助函数怎么构造的呢,下面是分析过程:

上面的解法大家肯定不熟悉,事实上用他解决一些问题会更加方便,常规还是泰勒
第三章:一元函数积分学:
考点1:计算不定积分、定积分、反常积分(简单)
考点2:变上限积分
知识点:(基本题)
f(x)在区间[a,b]上的平均值为x,啥意思?
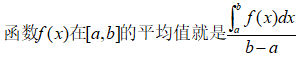
考点3:积分不等式
知识点一:(基本题)
凹曲线的几何特征:
如果曲线是凹的,连接曲线任意两点的这个弦,一定在这段曲线的上方
而曲线上任一点的切线,一定在这条曲线的下方
凸曲线的几何特征反过来,画个图就明白啦
题目一:
原题是一个选择题,我改一下,改成证明题,算是一个基本的不等式证明题吧

答案:

题目二:(难题)
类似的一道题目,来自网友:一半

答案:

经典错误答案(本人的,哈哈哈)
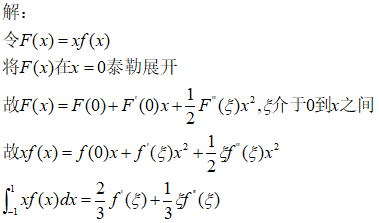
为什么错了呢?这个坑我记得我之前也犯过一次,傻了
正确答案:
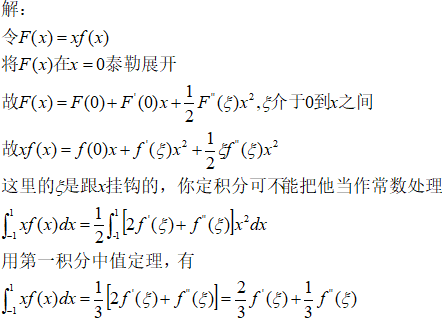
知识点二:(基本题)
目前遇到过常考的基本不等式,记住做题速度会更快,就不用再推导了
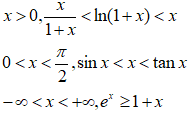
上述证明比较简单,第一个证明稍难一点,需要用到拉格朗日中值定理
第二不等式用画图来解释会比较容易,构造一个圆
第三个用单调性即可
考点4:定积分应用
知识点一:(基本题,但是容易出错!当年得分率为0.2左右)
定积分的几何意义:
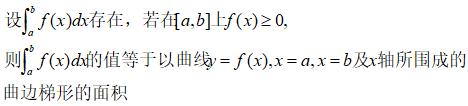
注意上面的f(x)是大于0的,算面积的时候要尤其注意
题目:
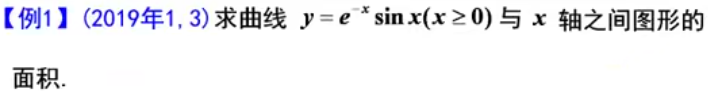
答案:
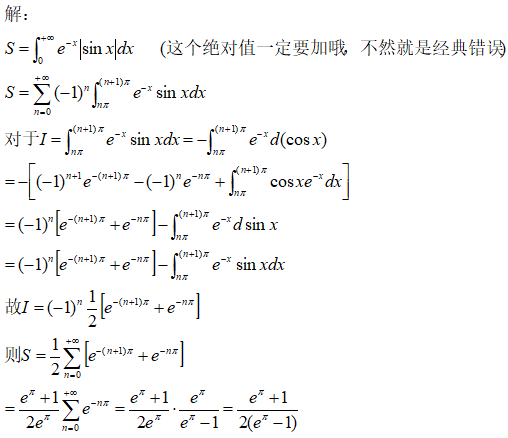
知识点二:(难题,考察相关变化率,因为考察的很少,所以觉得比较难)
这种题目知识点其实很少,只有多做几道题体会了~
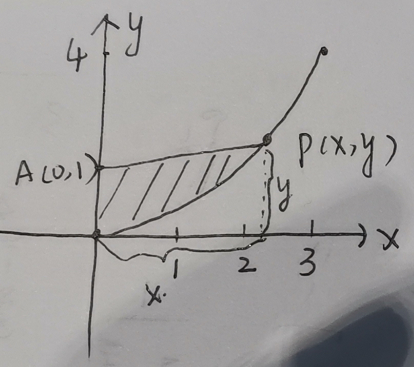
题目:

答案:


第四章:微分方程:
考点1:解方程(简单)
考点2:综合题
知识点一:(比较综合的填空题,事实上不难,但是得分率低)
导数定义+函数值与极限的关系+微分方程
题目:
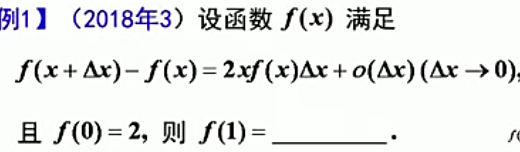
答案:

考点三 应用题(简单)
第五章:多元函数微分学:
考点一:求偏导求微分(简单)
考点二:极值与最值(未完)
我要放鸽子了,原本说好11月1号开始模拟卷更新的,但是我基础还差一点点,所以我跟着武忠祥把基础过了一遍;大概明天能把武忠祥真题班讲义做完,还是蛮有收获的~到时候我把笔记弄成pdf,我喜欢把自己笔记打印下来,蛮有成就感~然后具体的规划是这样,叫做11月绝对计划:11月8日开始,每天一套模拟,差不多12月6号能把李正元,李林,李永乐,汤家凤的做完;然后就只剩下张宇的12套卷,这个卷子我倒是可做可不做的,根据复习情况再来做~11月1,2号真题班讲义,11月3,4,5把剩下的三套真题总结一下;11月6,7号把所有错题全部拉一遍,然后进入冲刺模拟!最后
以上就是顺利绿草最近收集整理的关于多元函数严格凹 海塞矩阵正定_武忠祥真题班归纳(更新至多元函数微分学)...的全部内容,更多相关多元函数严格凹内容请搜索靠谱客的其他文章。








发表评论 取消回复