概述
复习一下哈夫曼树和哈夫曼编码
举个例子
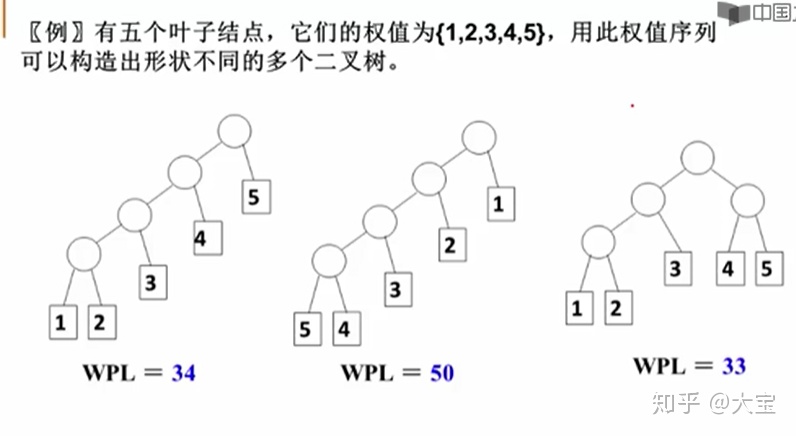
构造效率最好的搜索树
权重就是频率，叶子节点的长度就是搜索次数
事件出现次数*搜索次数=此事件进行的搜索次数
WPL就是所有事件的搜索次数，出现频率高的事件要靠近树根
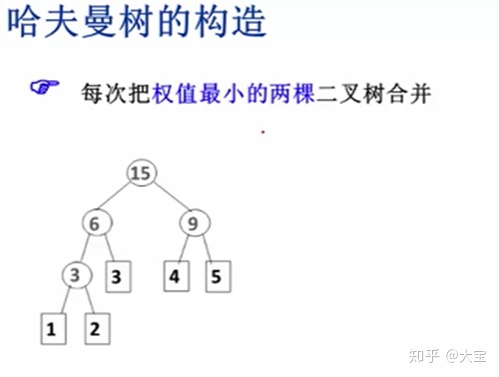
把权重从小到大排序，挑两个最小的合并成一棵树，权重相加作为根节点
这个根节点跟剩下的权重一起排序，选出两个最小的继续合并
构造哈夫曼树O(NlogN)
自己写的
HuffManTree这是ppt上的，我有点没看懂
typedef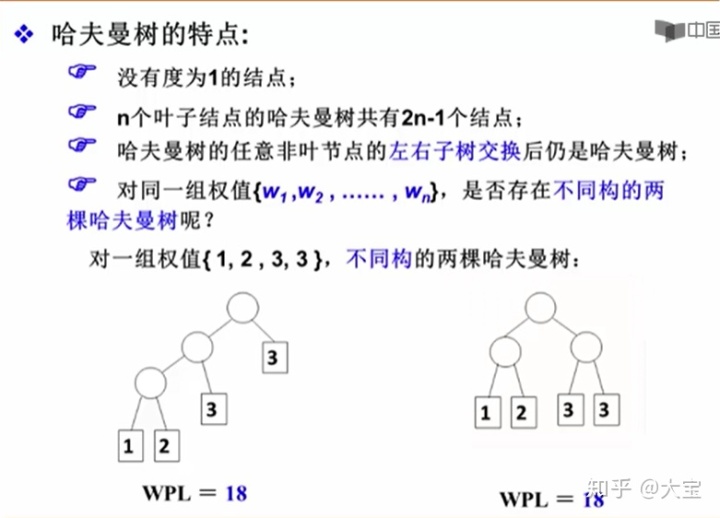 
所有元素都在叶节点上
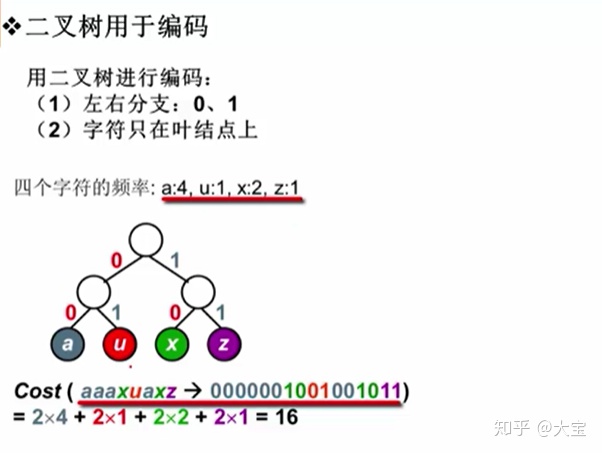
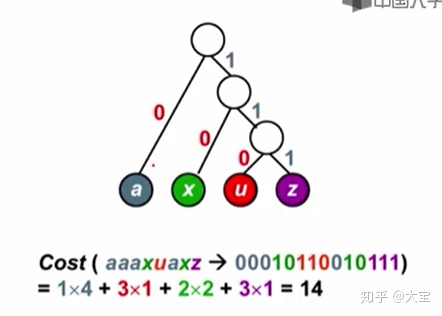
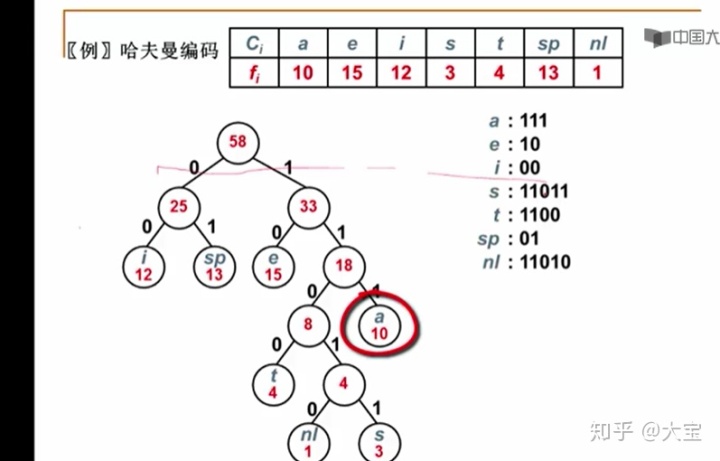
练习题：Huffman Codes
Sample Input:
7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11Sample Output:
Yes
Yes
No
No给出一组字母的权重，判断所给编码满不满足哈夫曼编码的条件：
- WPL最小
- 所有的字母都在叶节点上
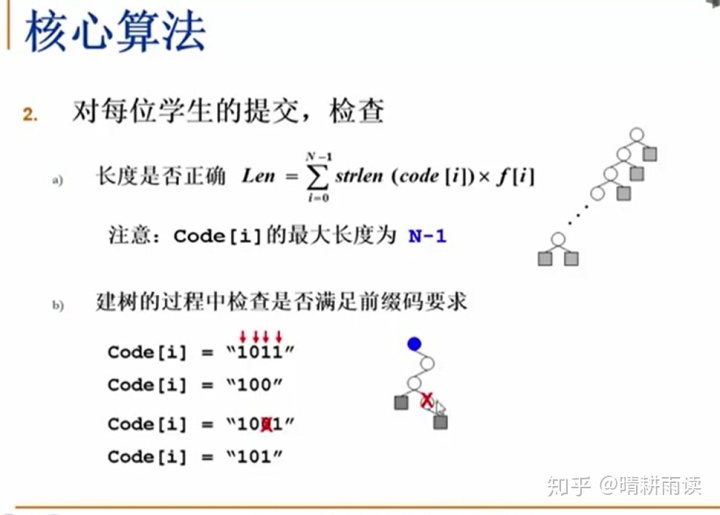
- 定义HuffManTree
int - 计算一个HuffmanTree的WPL
int - 定义小顶堆
class - 一种huffman编码的结构
//定义huffman编码的结构
- 主要算法，判断一种编码是不是符合huffman编码的条件
bool - 主函数
int 最后
以上就是等待手套为你收集整理的huffman树_数据结构：树—哈夫曼树（练习题Huffman Codes）的全部内容，希望文章能够帮你解决huffman树_数据结构：树—哈夫曼树（练习题Huffman Codes）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复