图的遍历:深度优先、广度优先
遍历
图的遍历是指从图中的某一顶点出发,按照一定的策略访问图中的每一个顶点。当然,每个顶点有且只能被访问一次。
在图的遍历中,深度优先和广度优先是最常使用的两种遍历方式。这两种遍历方式对无向图和有向图都是适用的,并且都是从指定的顶点开始遍历的。先看下两种遍历方式的遍历规则:
深度优先
深度优先遍历也叫深度优先搜索(Depth First Search)。它的遍历规则:不断地沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。
具体点,给定一图G=<V,E>,用visited[i]表示顶点i的访问情况,则初始情况下所有的visited[i]都为false。假设从顶点V0开始遍历,则下一个遍历的顶点是V0的第一个邻接点Vi,接着遍历Vi的第一个邻接点Vj,……直到所有的顶点都被访问过。
所谓的第一个是指在某种存储结构中(邻接矩阵、邻接表),所有邻接点中存储位置最近的,通常指的是下标最小的。在遍历的过程中有两种情况经常出现
- 某个顶点的邻接点都已被访问过的情况,此时需回溯已访问过的顶点。
- 图不连通,所有的已访问过的顶点都已回溯完了,仍找不出未被访问的顶点。此时需从下标0开始检测visited[i],找到未被访问的顶点i,从i开始新一轮的深度搜索。
看一个例子
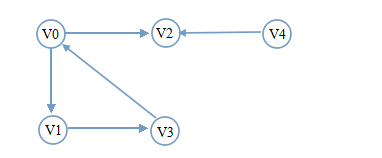
从V
0
开始遍历
遍历分析:V0有两个邻接点V1和V2,选择下标最小的V1遍历。接着从V1开始深度遍历,V1只有邻接点V3,也就是没有选的:遍历V3。接着从V3开始遍历,V3只有邻接点V0,而V0已经被遍历过。此时出现了上面提到的情况一,开始回溯V1,V1无未被遍历的邻接点,接着回溯V0,V0有一个未被遍历的邻接点V2,新的一轮深度遍历从V2开始。V2无邻接点,且无法回溯。此时出现了情况二,检测visited[i],只有V4了。深度遍历完成。看到回溯,应该可以想到需要使用栈。
遍历序列是
V0->V1->V3->V2->V4。
从其它顶点出发的深度优先遍历序列是:
V1->V3->V0->V2->V4。
V2->V0->V1->V3->V4。
V3->V0->V1->V2->V4。
V4->V2->V0->V1->V3。
以上结果,我们稍后用于测试程序。
结合在图的实现:邻接矩阵中的代码,我们看下在邻接矩阵形式下的图的深度遍历算法:
深度优先代码
其它代码前面已经见过,就不给出了,下面看下图的广度遍历。深度遍历和广度遍历的测试,稍后一并给出。
广度优先
广度优先遍历也叫广度优先搜索(Breadth First Search)。它的遍历规则:
- 先访问完当前顶点的所有邻接点。(应该看得出广度的意思)
- 先访问顶点的邻接点先于后访问顶点的邻接点被访问。
具体点,给定一图G=<V,E>,用visited[i]表示顶点i的访问情况,则初始情况下所有的visited[i]都为false。假设从顶点V0开始遍历,且顶点V0的邻接点下表从小到大有Vi、Vj...Vk。按规则1,接着应遍历Vi、Vj和Vk。再按规则2,接下来应遍历Vi的所有邻接点,之后是Vj的所有邻接点,...,最后是Vk的所有邻接点。接下来就是递归的过程...
在广度遍历的过程中,会出现图不连通的情况,此时也需按上述情况二来进行:测试visited[i]...。
在上述过程中,可以看出需要用到队列。
举个例子,还是同样一幅图:

从V
0
开始遍历
遍历分析:V0有两个邻接点V1和V2,于是按序遍历V1、V2。V1先于V2被访问,于是V1的邻接点应先于V2的邻接点被访问,那就是接着访问V3。V2无邻接点,只能看V3的邻接点了,而V0已被访问过了。此时需检测visited[i],只有V4了。广度遍历完毕。
遍历序列是
遍历序列是
V0->V1->V2->V3->V4。
从其它顶点出发的广度优先遍历序列是
V1->V3->V0->V
2
->
V
4
。
V2->V0->V1->V3->V4。
V3->V0->V1->V2->V4。
V4->V2->V0->V1->V3。
以上结果,我们同样用于测试程序。
在邻接矩阵下,图的广度遍历算法
广度优先代码
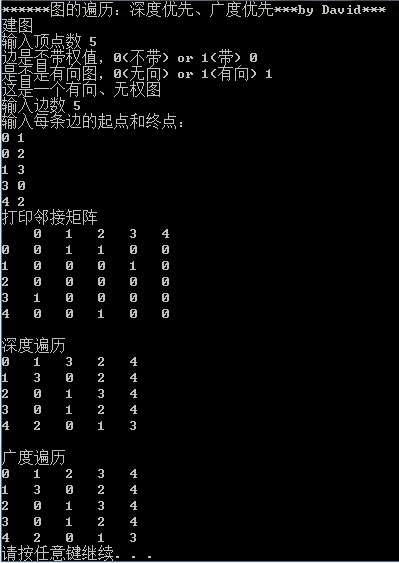
仔细对照测试结果,我们的代码是没有问题的。
完整代码下载:图的遍历:深度优先、广度优先
小结
对于某个图来说,深度优先遍历和广度优先遍历的序列不是唯一的,但当图的存储结构一确定,它的遍历序列就是唯一的。因为当有多个候选点时,我们总是优先选择下标最小的。
专栏目录:
- 数据结构与算法目录
- c指针
转载自:数据结构:图的遍历--深度优先、广度优先
最后
以上就是羞涩人生最近收集整理的关于数据结构:图的遍历--深度优先、广度优先的全部内容,更多相关数据结构:图内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复