循环队列 (顺序存储)

数组 和 链表是最基本的数据结构，栈、队列、树、图等复杂数据结构都是基于数组或链表方式存储

队列(Queue)特征：

• 循环队列的顺序存储是基于数组来实现的

• 队列是一种操作受限的线性表。队列只能在表的一端进行插入操作，在另一端进行删除操作。其中，允许插入的一端叫队尾，允许删除的一端叫队头。【遵守: 先进先出(First In First Out，FIFO) 规则，例如元素A、B、C、D依次入队，则出队顺序也必须是A、B、C、D】

注意咯：很多初学者都容易将 队头 和 队尾 搞混，以为元素是在队头插入在队尾删除。

循环队列特征：

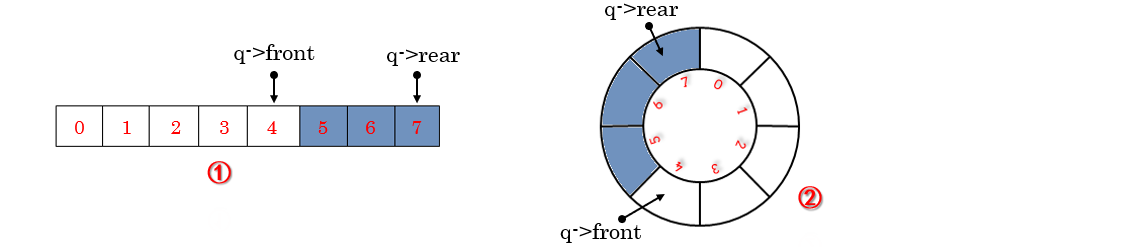
• 循环队列是对队列的一种改进，主要是为了解决队尾溢出而实际上数组仍有空余空间这种“假溢出”（如图一）问题

• 循环队列的rear和front到达队尾端点，能折回数组开始处。相当于将数组首尾相连，想象 成环状（如图二）。

头指针Front 和 尾指针Rear：

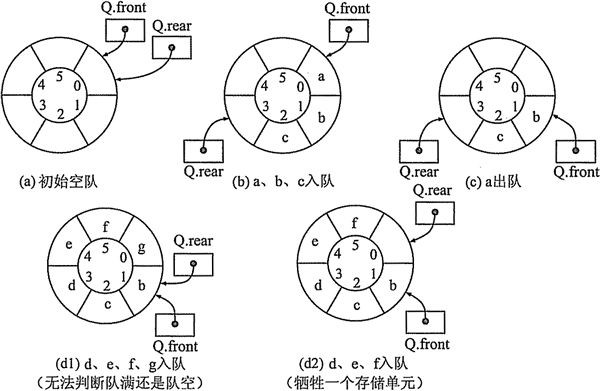
• 循环队列中，一般头指针front指向队头元素，尾指针rear指向队尾元素的下一个元素；或者 头指针front指向队头元素的下一个元素，尾指针rear指向队尾元素。 这样的目的是满足front == rear判空条件

循环队列 - 结构体

#define MAX_SIZE 255 //循环队列的最大容量

typedef struct C_Queue {
	int data[MAX_SIZE];  //指定循环队列大小
	int front;       //循环队列头指针
	int rear;	//循环队列尾指针
} *Queue;


注意：结构体后面的*Queue是指向C_Queue的结构体指针，
如果不加*，使用结构体指针需要Queue *q这样，
加了*，使用结构体指针，只需Queue q即可；

循环队列 - 创建

• 【通过malloc()函数动态创建一个循环队列】

Queue queue_create() {
	Queue q = (Queue)malloc(sizeof(C_Queue)); //给循环队列分配内存空间
	q->front = q->rear = 0;  //初始状态下，头指针和尾指针 均指向0(下标)

	return q;
}

循环队列 - 判空

boolean queue_empty(Queue q) {
	if (q->front == q->rear) {  //当front和rear相等时，队列为空
		return TRUE;
	} else {
		return FALSE;
	}
}

循环队列 - 判满

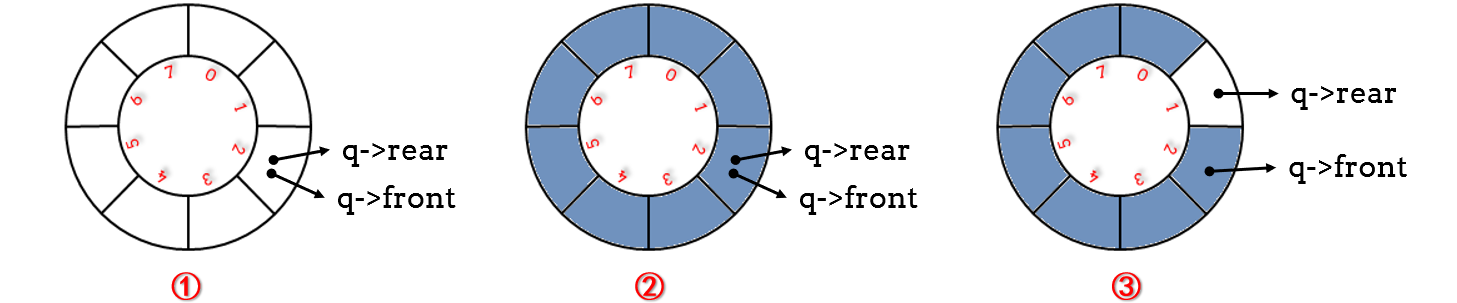
• rear 和 front的值相等时（图一和图二），队列可能出现队空或队满两种情况，从而无法判别队满还是队空。

• 针对这一问题，解决方法有两种：

    1. 定义一个变量size来记录当前队列的元素个数【队尾插入一个元素，size+1； 队头删除一个元素，size-1】

    2. 牺牲一个存储单元（如图三），在队尾指针rear+1就能赶上队头指针front时，我们就认为队满了。【即：循环队列最大实际长度 = MAX_SIZE - 1】，这种方法的队满条件是：(q->rear+1)%MAX_SIZE == q->front 【记得%MAX_SIZE取模 ，否则可能会超出数组最大下标】，下面用的就是这种方法。

boolean queue_full(Queue q) {
	if ((q->rear + 1) % MAX_SIZE == q->front) {
		return TRUE;
	} else {
		return FALSE;
	}
}

循环队列 - 求长度

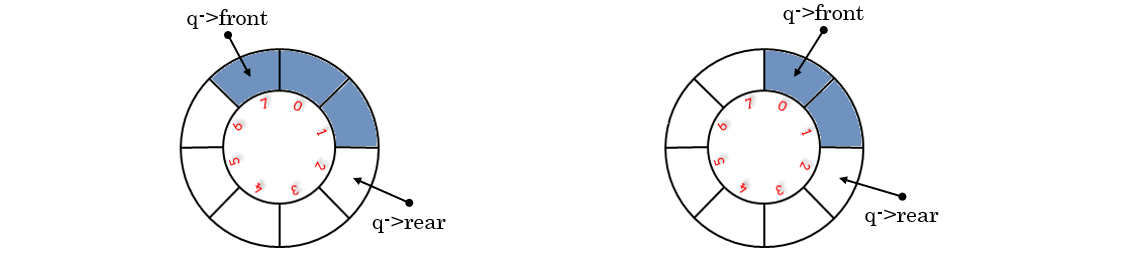
• 【由图可知：MAX_SIZE = 8，q->rear = 1，q->front = 3，队列长度length = 6】

• 验证一下：(q->rear - q->front + MAX_SIZE) % MAX_SIZE; 是不是可以求队列长度。（length = (1 - 3 + 8) % 8 = 6，没毛病）
  

int queue_length(Queue q) {
	return (q->rear - q->front + MAX_SIZE) % MAX_SIZE;
}

循环队列 - 入队

• 队尾插入元素，入队前要先判断循环队列是否已满

• 先将待入队的元素，插入尾指针原本指向的位置

• 尾指针rear + 1，并%MAX_SIZE取模。【模MAX_SIZE后，当尾指针指向数组下标最大值时，可以让尾指针折回数组开始处】

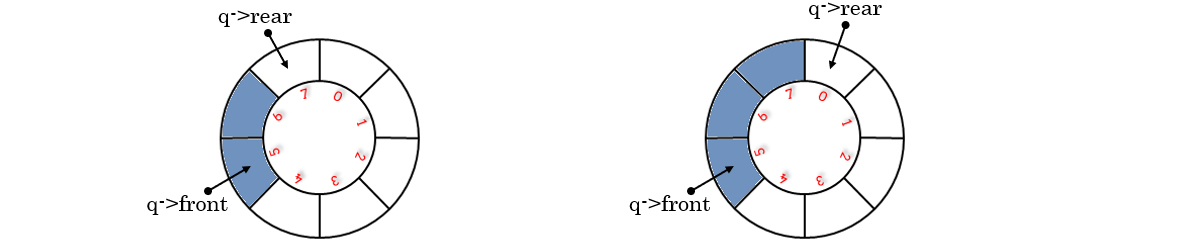
boolean queue_rear_insert(Queue q, int x) {
	if (queue_full(q)) { //判断队满
		printf("队列已满！n");
		return FALSE;
	} else {
		q->data[q->rear] = x; //先将元素插入尾指针原本指向的位置
		q->rear = (q->rear + 1) % MAX_SIZE; //尾指针+1
		return TRUE;
	}
}

循环队列 - 出队

• 队头删除元素，出对前要先判断循环队列是否为空

• 用x记录，要出队元素的值，作为函数的返回值

• 头指针front + 1，并%MAX_SIZE取模。【模MAX_SIZE后，当头指针指向数组下标最大值时，可以让头指针折回数组开始处】

int queue_front_delete(Queue q) {
	int x;
	if (queue_empty(q)) {
		printf("队列无元素可删除！n");
		return 0;
	} else {
		x = q->data[q->front];  //用x记录头指针指向的元素值
		q->front = (q->front + 1) % MAX_SIZE;  //头指针front + 1，并%MAX_SIZE取模
		return x;
	}
}

循环队列 - 获取队头元素

int queue_get_front(Queue q) {
	if (!queue_empty(q)) {
		return q->data[q->front];
	}
	return 0;
}

循环队列 - 迭代

• 将循环队列中所有元素出队，并输出

void queue_items_printf(Queue q) {
	while (!(q->front == q->rear)) {
		printf("%d ", q->data[q->front]);  //输出头指针front指向元素的值
		q->front = (q->front + 1) % MAX_SIZE;  //头指针front + 1
	}
}

整个程序代码

#include <stdio.h>
#include <stdlib.h>

typedef enum {FALSE, TRUE} boolean;

#define MAX_SIZE 8 //循环队列的最大长度

//结构体
typedef struct C_Queue {
	int data[MAX_SIZE];  //指定循环队列大小
	int front;       //循环队列头指针
	int rear;	//循环队列尾指针
} *Queue;

//创建队列
Queue queue_create() {
	Queue q = (Queue)malloc(sizeof(C_Queue)); //给循环队列分配内存空间
	q->front = q->rear = 0;  //初始状态下，头指针和尾指针 均指向0(下标)
	if (q == NULL) { //内存分配失败
		return NULL;
	}
	return q;
}

//队列判空
boolean queue_empty(Queue q) {
	if (q->front == q->rear) {  //当front和rear相等时，队列为空
		return TRUE;
	} else {
		return FALSE;
	}
}

//队列判满
boolean queue_full(Queue q) {
	if ((q->rear + 1) % MAX_SIZE == q->front) {
		return TRUE;
	} else {
		return FALSE;
	}
}

//队列长度
int queue_length(Queue q) {
	return (q->rear - q->front + MAX_SIZE) % MAX_SIZE;
}

//队尾插入元素
boolean queue_rear_insert(Queue q, int x) {
	if (queue_full(q)) {
		printf("队列已满！n");
		return FALSE;
	} else {
		q->data[q->rear] = x;
		q->rear = (q->rear + 1) % MAX_SIZE;
		return TRUE;
	}
}

//队头删除元素
int queue_front_delete(Queue q) {
	int x;
	if (queue_empty(q)) {
		printf("队列无元素可删除！n");
		return 0;
	} else {
		x = q->data[q->front];
		q->front = (q->front + 1) % MAX_SIZE;
		return x;
	}
}

//获取队头元素
int queue_get_front(Queue q) {
	if (!queue_empty(q)) {
		return q->data[q->front];
	}
	return 0;
}


//将队列所有元素出队
void queue_items_printf(Queue q) {
	while (!(q->front == q->rear)) {
		printf("%d ", q->data[q->front]);
		q->front = (q->front + 1) % MAX_SIZE;
	}
}


int main() {
	/* 创建一个循环队列 */
	Queue q = queue_create();
	int A[8], i;

	if (NULL == q) {
		printf("队列创建失败！n");
		return -1;
	}

	printf("当前队列长度为：%dn", queue_length(q));

	printf("输入要入队的元素: ");
	for (i = 0; i < 8; i++) {
		scanf("%d", &A[i]);
	}
	//将数组中的元素按顺序插入循环队列
	for (i = 0; i < 8 ; i++) {
		queue_rear_insert(q, A[i]);
	}
	printf("当前队头元素为：%dn", queue_get_front(q));
	printf("n当前队列长度为：%dn", queue_length(q));


	printf("n队列元素出队顺序：");
	//将循环队列所有元素出队，并输出
	queue_items_printf(q);
	printf("n当前队列长度为：%dn", queue_length(q));

	return 0;
}

循环队列总结：

1. 循环队列的两个状态

• 队空状态：q->front = q->rear

• 队满状态：(q->rear + 1) % MAX_SIZE = q->front

2. 循环队列的三个操作

• 求队列长度：length = (q->rear - q->front + MAX_SIZE) % MAX_SIZE

• 元素 x 入队：q->data[q->rear] = x ;   q->rear = (q->rear + 1) % MAX_SIZE ;

• 元素 x 出队：x = q->data[q->front] ;   q->front = (q->front + 1) % MAX_SIZE ;

来几道题目巩固下

1. 循环队列存储在数组A[0…n]中，则入队时的操作为：__ rear = (rear+1) mod (n+1) __

• 解析：因为数组下标是从0开始的，所以数组的最大容量为n+1，即循环队列的MAX_SIZE = n+1，入队操作为：(q->rear + 1) % MAX_SIZE = (rear + 1) mod (n + 1) 【mod是%的意思，N mod M = N % M】

2. 已知循环队列的存储空间为数组A[21]，front指向队头元素的前一个位置，rear指向队尾元素，假设当前front和rear的值分别为8和3，则该队列的长度为：__ 16 __

• 解析：length = (q->rear - q->front + MAX_SIZE) % MAX_SIZE = (3 - 8 + 21) % 21 = 16

循环队列JAVA语言实现

最后

以上就是悦耳大地为你收集整理的循环队列 (顺序存储)的全部内容，希望文章能够帮你解决循环队列 (顺序存储)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。