概述
一、前言
我们介绍一个非常有用的函数：sigmoid函数，它们在机器学习中经常用到。尤其是在神经网络中，经常用于作为隐藏层神经元的输出函数。
二、sigmoid函数
sigmoid函数也叫Logistic函数，它可以将一个实数映射到(0,1)的区间。
函数表示如下：
f
(
x
)
=
1
1
+
e
−
x
f(x)=frac1{1+e^{-x}}
f(x)=1+e−x1
当
x
=
0
x=0
x=0时，
f
(
x
)
=
0.5
f(x)=0.5
f(x)=0.5
其导数为
f
′
(
x
)
=
f
(
x
)
(
1
−
f
(
x
)
)
f'(x)=f(x)(1-f(x))
f′(x)=f(x)(1−f(x))
证明如下：
f
(
x
)
=
1
1
+
e
−
x
=
(
1
+
e
−
x
)
−
1
f(x)=frac1{1+e^{-x}}=(1+e^{-x})^{-1}
f(x)=1+e−x1=(1+e−x)−1
f ′ ( x ) = − ( 1 + e − x ) − 2 e − x ( − 1 ) = e − x ( 1 + e − x ) 2 = 1 + e − x − 1 ( 1 + e − x ) 2 = 1 1 + e − x − 1 ( 1 + e − x ) 2 = ( 1 1 + e − x ) ( 1 − 1 1 + e − x ) = f ( x ) ( 1 − f ( x ) ) begin{aligned} f'(x) &=-(1+e^{-x})^{-2}e^{-x}(-1)\ &=frac{e^{-x}}{(1+e^{-x})^2}\ &=frac{1+e^{-x}-1}{(1+e^{-x})^2}\ &=frac{1}{1+e^{-x}}-frac{1}{(1+e^{-x})^2}\ &=(frac{1}{1+e^{-x}}) (1-frac{1}{1+e^{-x}})\ &=f(x)(1-f(x)) end{aligned} f′(x)=−(1+e−x)−2e−x(−1)=(1+e−x)2e−x=(1+e−x)21+e−x−1=1+e−x1−(1+e−x)21=(1+e−x1)(1−1+e−x1)=f(x)(1−f(x))
三、代码实现绘图
用matplotlib绘制函数图像：
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
x = np.arange(-10, 10, 0.1) #起点，终点，间距
y = sigmoid(x)
plt.plot(x, y)
plt.show()
运行结果：
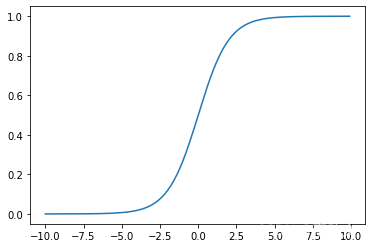
四、参考资料
《Sigmoid函数求导过程》
最后
以上就是幸福冰棍为你收集整理的sigmoid函数及其图像绘制一、前言二、sigmoid函数三、代码实现绘图四、参考资料的全部内容，希望文章能够帮你解决sigmoid函数及其图像绘制一、前言二、sigmoid函数三、代码实现绘图四、参考资料所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复