数据探索
- 数据挖掘中特别的列
- 只有一种值的列:
- 列的值各不相同:
- 派生变量:
- 异常值分析
- 3 σ 3{sigma} 3σ原则
- 箱线图分析
- 一致性分析
- 数据特征分析
- 分布分析
- 定量数据的分布分析
- 定性数据分析
- 统计量分析
- 集中趋势度量
- 离中趋势度量
- 贡献度分析
- 相关性分析
- 计算相关系数
- matlab主要数据探索函数
- 统计特征函数
- 统计作图函数
- pie
- boxplot
- errorbar
- 参考文献
数据挖掘中特别的列
列或者字段代表了每条记录里的数据。
只有一种值的列:
单值的列对于区分不同行不包含任何信息,它们缺乏任何信息内容,在数据挖掘中应当被忽略。
列的值各不相同:
另一个极端是列在每一行上几乎都不相同,由于每一个记录上这些数值几乎不同,所以它们妨碍了数据挖掘算法从不同行间找出规律。
派生变量:
如:电话号码和地址包含地理信息;
发动机的识别号码包含了生产年份、制造商、型号和原产地等;
客户号码也可能知道哪些是最新客户;
重要的特性应该作为派生变量提取出来,而忽略原始列。
异常值分析
异常值是指样本中的个别值,其数值明显偏离其余的观测值。异常值也称为离群点。异常值分析也称为离群点分析。
3 σ 3{sigma} 3σ原则
如果数据服从正态分布,在 3 σ 3{sigma} 3σ原则下,异常值被定义为一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下,距离平均值 3 σ 3{sigma} 3σ之外的值出现的概率为 P ( ∣ x − μ ∣ > 3 σ ) < = 0.003 P(|x-{mu}|>3{sigma})<=0.003 P(∣x−μ∣>3σ)<=0.003
箱线图分析
异常值通常被定义为小于 Q L − 1.5 I Q R Q_L-1.5IQR QL−1.5IQR或大于 Q U + 1.5 I Q R Q_U+1.5IQR QU+1.5IQR的值。 Q L Q_L QL被称为下四分位数, Q U Q_U QU被称为上四分位数。 I Q R IQR IQR表示四分位数间距。是上四分位数与下四分位数的插值。
function []=loss_detecting(sales)
%% 缺失值检测,并打印结果
rows = size(sales,1);
%% 缺失值检测 并打印结果
nanvalue = find(isnan( sales));
if isempty(nanvalue) % 没有缺失值
disp('没有缺失值!');
else
rows_ = size(nanvalue,1);
disp(['缺失值个数为:' num2str(rows_) ',缺失率为:' num2str(rows_/rows) ]);
end
异常值检测函数:
function [] = abnormal_detecting(sales)
%% 异常值检测
% 箱形图上下界
q_= prctile(sales,[25,75]);
p25=q_(1,1);
p75=q_(1,2);
upper = p75+ 1.5*(p75-p25);
lower = p25-1.5*(p75-p25);
upper_indexes = sales(sales>upper);
lower_indexes = sales(sales<lower);
indexes =[upper_indexes;lower_indexes];
indexes = sort(indexes);
% 箱形图
figure
hold on;
boxplot(sales,'whisker',1.5,'outliersize',6);
rows = size(indexes,1);
flag =0;
for i =1:rows
if flag ==0
text(1+0.01,indexes(i,1),num2str(indexes(i,1)));
flag=1;
else
text(1-0.017*length(num2str(indexes(i,1))),indexes(i,1),num2str(indexes(i,1)));
flag=0;
end
end
hold off;
disp('数据缺失值及异常值检测完成!');
一致性分析
该问题主要集中在重复存放的数据未能进行一致性更新造成的。
数据特征分析
分布分析
能揭示数据的分布特征和分布类型。
定量数据的分布分析
对于定量、变量而言,选择组数和组宽是做频率分布分析时最主要的问题。
一般按照以下的步骤进行:
(1)求极差;
(2)决定组距和组数;
(3)决定分点;
(4)列出频率分布表;
(5)绘制频率分布直方图;
遵循的原则有:
(1)各组之间必须是相互排斥的;
(2)各组必须将所有的数据包含在内;
(3)各组的组宽最好相等。
定性数据分析
画出条形图和饼图。
统计量分析
集中趋势度量
(1)均值
一般采用加权均值;
截断均值是去掉高、低极端值后的平均数。
(2)中位数
将某一数据集
x
:
{
x
1
,
x
2
,
.
.
.
,
x
n
}
x:{{x_1,x_2,...,x_n}}
x:{x1,x2,...,xn}从小到大排序:
{
x
(
1
)
,
x
(
2
)
,
.
.
.
,
x
(
n
)
}
{x_{(1)},x_{(2)},...,x_{(n)}}
{x(1),x(2),...,x(n)}。
当n为奇数时,
M
=
x
(
n
+
1
2
)
M=x_{(frac{n+1}{2})}
M=x(2n+1)
当n为偶数时,
M
=
1
2
(
x
(
n
2
)
+
x
(
n
+
1
2
)
)
M=frac{1}{2}(x_{(frac{n}{2})}+x_{(frac{n+1}{2})})
M=21(x(2n)+x(2n+1))
(3)众数
众数是指数据集中出现最频繁的值。
离中趋势度量
(1)极差
(2)标准差
(3)变异系数
变异系数度量标准差相对于均值的离中程度。
C
V
=
s
x
‾
∗
100
CV=frac{s}{overline{x}}*100%
CV=xs∗100
(4)四分位数间距:
其值越大,说明数据的变异程度越大,反之,说明数据的变异程度越小。
% 众数
mode_ = mode(sales);
% 极差
range_ = range(sales);
% 四分位数间距
q1=prctile(sales,25);
q2=prctile(sales,75);
distance=q3-q1;
贡献度分析
贡献度分析又称帕累托分析,它的原理是帕累托法则,又称20/80定律。比如:对于一个公司来讲,80%的利润常常来自于20%最畅销的产品,而其它80%的产品只产生了20%的利润。
帕累托分析也可以称为累计占比分析。
function [] = dish_pareto(num)
%% 帕累托图作图
rows = size(num,1);
hold on;
% 计算累计系数
yy_ = cumsum(num(:,end));
yy=yy_/yy_(end)*100;
[hAx,hLine1,hLine2]=plotyy(1:rows,num(:,end),1:rows,yy,'bar','plot');
set(hAx(1),'XTick',[])%去掉x轴的刻度
set(hLine1,'BarWidth',0.5);
set(hAx(2), 'XTick', 1:rows);
set(hAx(2),'XTickLabel',raw(2:end,2));
ylabel(hAx(1),'盈利:元') % left y-axis
ylabel(hAx(2),'累计百分比:%') % right y-axis
set(hLine2,'LineStyle','-')
set(hLine2,'Marker','d')
% 标记 80% 点
index = find(yy>=80);
plot(index(1),yy(index(1))*100,'d', 'markerfacecolor', [ 1, 0, 0 ] );
text(index(1),yy(index(1))*93,[num2str(yy(index(1))) '%'] );
hold off;
disp('餐饮菜品盈利数据帕累托图作图完成!');
相关性分析
计算相关系数
(1)Pearson相关系数
一般用于分析两个连续型变量之间的关系。
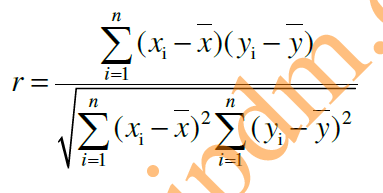
相关系数的取值范围:-1<=r<=1

(2)Spearman秩相关系数
Pearson线性相关系数要求连续变量的取值服从正态分布。不服从正态分布的变量,分类或等级变量至今的关联性可采用Spearman秩相关系数。
计算公式:
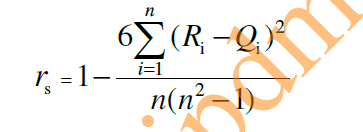
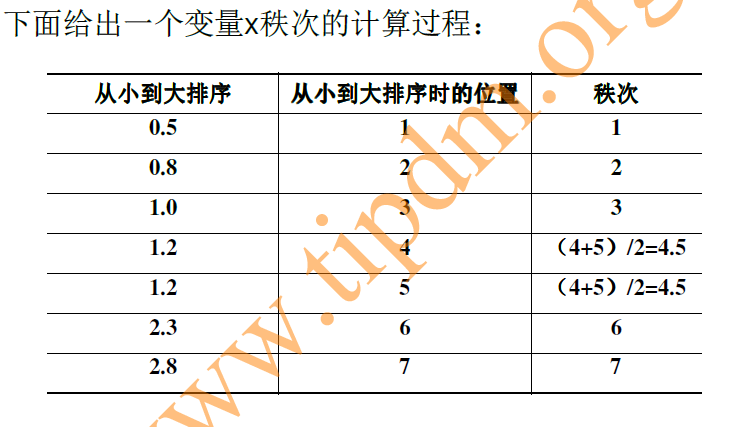
对两个变量成对的取值分别按照从小到大(或者从大到小的顺序)编秩。
R
i
R_i
Ri代表
x
i
x_i
xi的秩次,
Q
i
Q_i
Qi代表
y
i
y_i
yi的秩次。
R
i
−
Q
i
R_i-Q_i
Ri−Qi为
x
i
,
y
i
x_i,y_i
xi,yi的秩次之差。
(3)判定系数
它是相关系数的平方,用
r
2
r^2
r2表示;用来衡量回归方程对y的解释程度。
r
2
r^2
r2越接近于1,表明x与y之间的相关性越强;
r
2
r^2
r2越接近于0,表明两个变量之间几乎没有直线相关关系。
matlab主要数据探索函数
统计特征函数
MATLAB主要的统计特征函数
| 函数名 | 函数功能 |
|---|---|
| mean() | 计算数据样本的算术平均数 |
| geomean() | 计算数据样本的几何平均数 |
| var() | 计算数据样本的方差 |
| std() | 计算数据样本对的标准差 |
| corr() | 计算数据样本的spearman(Pearson)相关系数矩阵 |
| cov() | 计算数据样本的协方差矩阵 |
| moment() | 计算数据样本的指定阶中心距 |
几点说明:
var
使用格式:v=var(X),计算样本X的方差v。若X为向量,则计算向量的样本方差;若X为矩阵,则v为X的各列向量的样本方差构成的行向量。
corr
使用格式:R=corr(x,y,‘name’,‘value’),计算列向量x,y的相关系数矩阵R。
| name | value | 说明 |
|---|---|---|
| Type | pearson | 皮尔森相关系数 |
| Type | Kendall | 卡德尔系数 |
| Type | Spearman | 斯皮尔曼系数 |
| Rows | all | 全部数据,默认选项 |
| Rows | complete | 只使用没有缺失值的行 |
| Rows | pairwise | 计算R(i,j)只使用第i和j列中没有缺失值的数据 |
(6)cov
使用格式:R=cov(X),计算样本X的协方差矩阵R。样本X可为向量或矩阵。当X为向量时,R表示X的方差;当X为矩阵时,cov(X)计算方差矩阵。
R=cov(x,y)。函数等价于cov([x,y])。参数x,y为长度相等的列向量。
(7)moment
使用格式:m=moment(X,order)计算样本X的order阶次的中心矩m,参数order为正整数。样本X可为向量、矩阵或多维数组。
说明:一阶中心矩为0,二阶中心矩为用除数n得到的方差。其中n为向量X的长度或矩阵X的行数。
统计作图函数
| 作图函数名 | 作图函数功能 |
|---|---|
| pie() | 绘制饼形图 |
| hist() | 绘制二维条形直方图 |
| boxplot() | 绘制样本数据的箱线图 |
| errorbar() | 绘制误差条形图 |
pie
使用格式:pie(X).绘制矩阵X中非负数据的饼形图。若X中非负元素和小于1,则函数仅画出部分饼形图,且非负元素X(i,j)的值直接限定饼形图中扇形大小;若X中非负元素和大于等于1,则非负元素X(i,j)代表饼形图中扇形大小通过X(i,j)/Y的大小来决定,其中Y为矩阵X非负元素和。
例题:
x=[1,3,1.5,4,1.5];
explode=[1,0,0,0,0];% 第一个元素为1表示饼图中第一部分分离出来
pie(x,explode); % 画出饼形图
boxplot
使用格式:boxplot(X,notch),绘制矩阵样本X的箱型图。notch=1时,绘制矩阵样本X的带刻槽的凹盒图。参量notch=0时,绘制矩阵样本X的无刻槽的矩形箱型图。
x1=normrnd(4,5,100,1);
x2=normrnd(8,6,100,1);
boxplot([x1,x2],1);
errorbar
使用格式:errorbar(X,Y,L,U),绘制误差条形图。参量X,Y,L,U必须为同型向量或矩阵。若同为向量则在点(X(i),Y(i))画出向下长为L(i),向上长为U(i)的误差棒;若同为矩阵,则在点(X(i,j),Y(i,j))处画出向下长为L(i,j),向上长为U(i,j)的误差棒。
x=0:pi/10:pi;
y=2*x.*sin(x);
e=std(y).*ones(size(x)); % 产生误差棒长度
errorbar(x,y,e,e);
参考文献
张良均等. MATLAB数据分析与挖掘实战. 机械工业出版社,2015.
最后
以上就是霸气牛排最近收集整理的关于数据挖掘与分析(基于MATLAB)——数据探索数据挖掘中特别的列异常值分析数据特征分析matlab主要数据探索函数的全部内容,更多相关数据挖掘与分析(基于MATLAB)——数据探索数据挖掘中特别内容请搜索靠谱客的其他文章。








发表评论 取消回复