绘制图形的几个函数用法
例:绘制函数图形 f = xsin(10* pi*x)+1,区间[0,2];
plot()
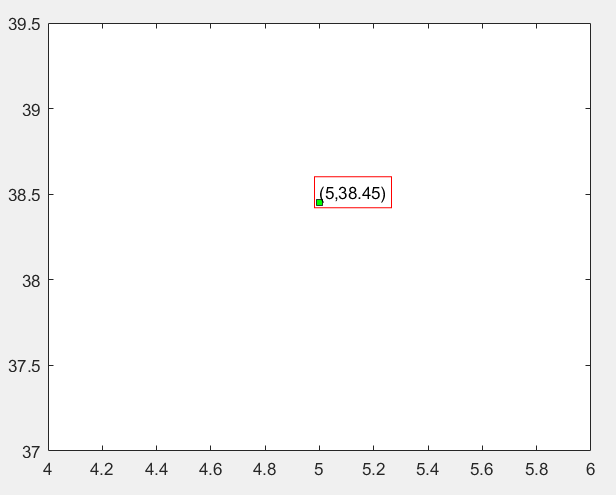
显示已知点的坐标:
plot(5,38.45,'rs','MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',5)
text(5,38.45,'(5,38.45)','EdgeColor','red','VerticalAlignment','bottom');
x=[0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39];
y2=[0 3.75 10.95 19.95 29.3 38.45 46.85 54.50 61.55 68.00 73.85 78.95 83.75 88.25 92.3 95.9 99.2 102.2 104.9 107.3 109.55 111.65 113.6 115.4 117.05 118.55 119.9 121.1 122.15 123.05 123.8 124.4 124.85 125.25 125.61 125.91 126.11 126.26 126.36 126.44];
plot(x,y2);
hold on;
y3=126.44;
plot(x,y3,'-');
% Set up fittype and options.
ft = 'linearinterp';
opts = fitoptions( ft );
opts.Normalize = 'on';
% Fit model to data.
fitresult = fit( x', y2', ft, opts );
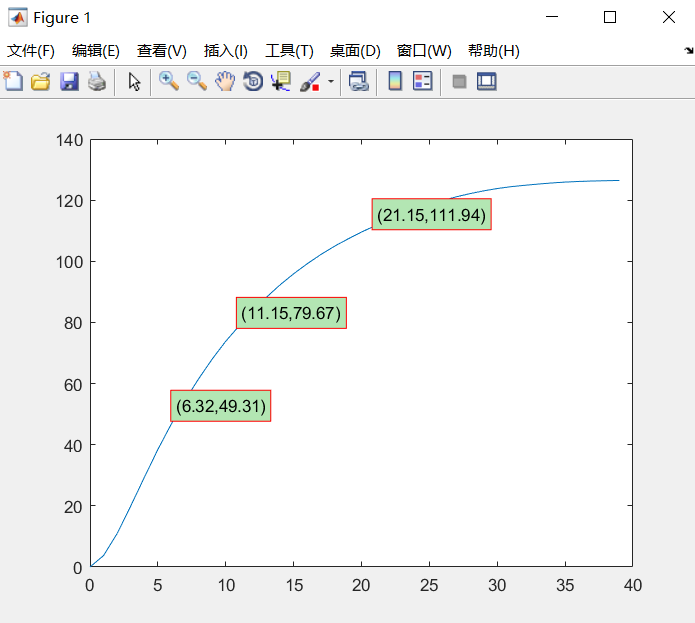
xx1 = [6.321,11.15,21.15]; % x = [6.321,11.15,21.15]
yy1 = fitresult( xx1 ); % 与x对应的y值
% 画点 标注
for i = 1:length(xx1)
plot(xx1(i),yy1(i),'rs','MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',6)
text(xx1(i),yy1(i),['(',num2str(xx1(i),'%5.2f'),',',num2str(yy1(i),'%5.2f'),')'],'EdgeColor','red','BackgroundColor',[.7 .9 .7],'VerticalAlignment','bottom');
end
- plot()
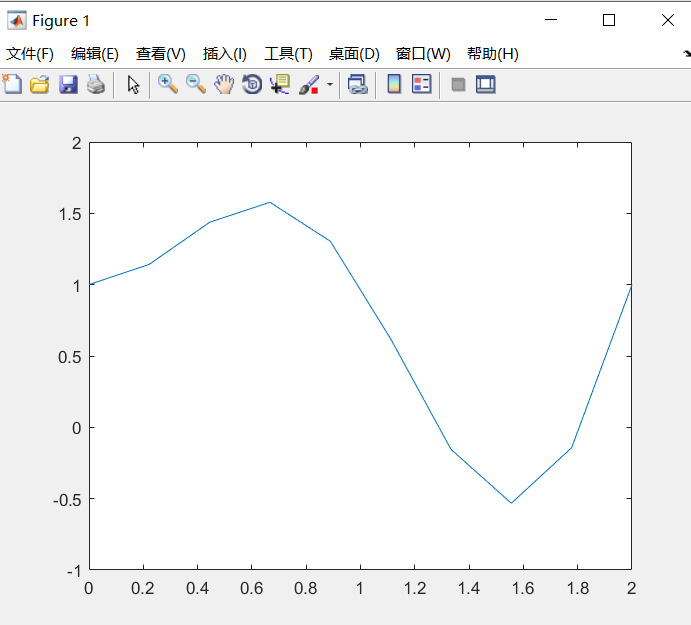
x=linspace(0,2,10); %将区间[0,10]划分为1000小区间
y=x.*sin(10*pi*x)+1;
plot(x,y) %以x元素为横坐标值,y元素为纵坐标值绘制图形
x=linspace(0,2,1000); %将区间[0,10]划分为1000小区间
y=x.*sin(10*pi*x)+1;
plot(x,y) %显示图形
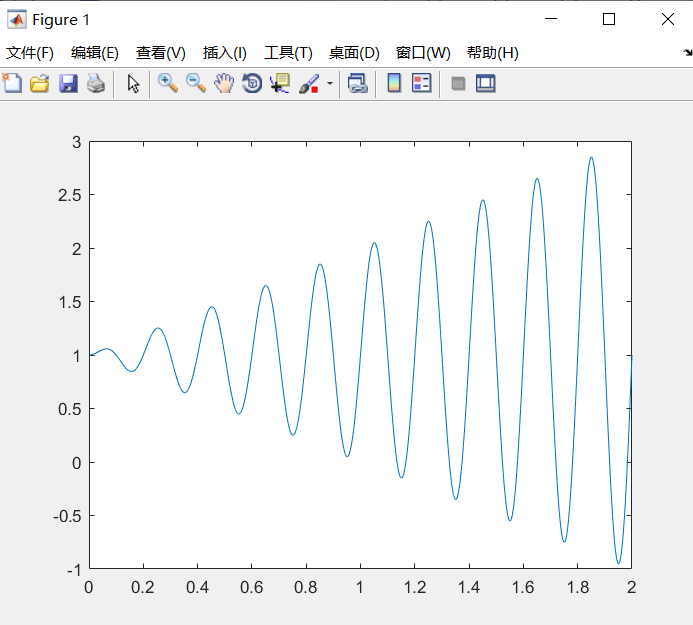
通过对比上下两张图可以发现,划分的区间越小,即划分越细,弧线越圆滑,图形拟合得越好。
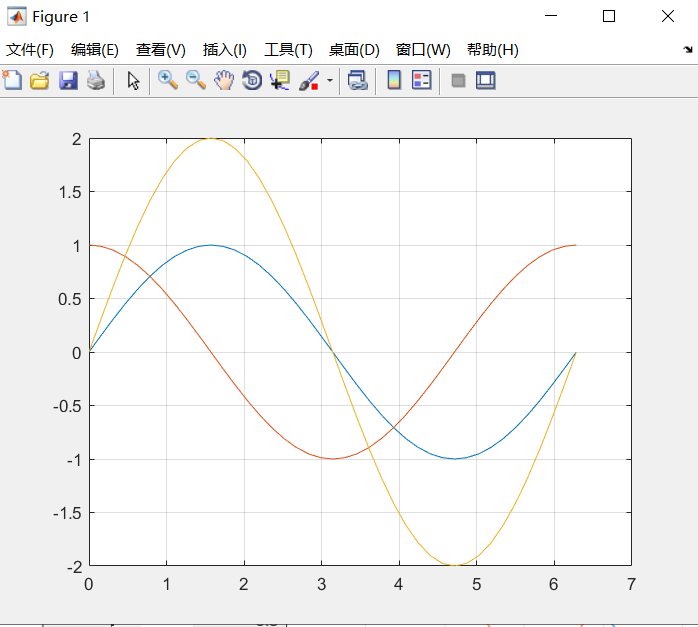
- 含多个输入参数的plot函数还可以同时绘制多条曲线,如果输入是矩阵的话,配对的x,y分别是矩阵的列元素,曲线条数等于矩阵列数。
x=0:pi/20:2*pi; %x的区间是0-2*pi,pi/20是步长
y1=sin(x);
y2=cos(x);
y3=2*sin(x);
x=[x;x;x]';
y=[y1;y2;y3]';
plot(x,y)
grid on %给图像加上栅格
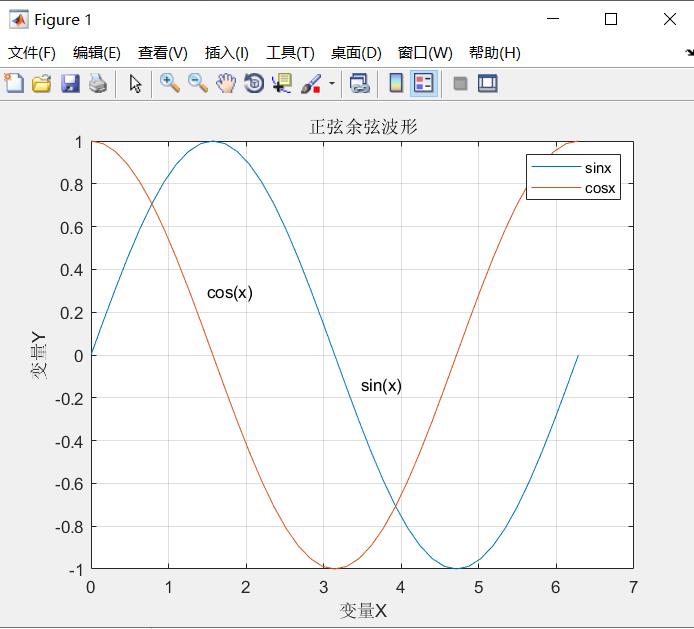
- 图形标注
%添加坐标轴信息
xlabel('变量 X')
ylabel('变量 Y1 & Y2')
title('正弦余弦波形') %添加图像标题
text(1.5,0.3,'cos(x)') %将cosx这个注解加到坐标中的某个位置
gtext('sin(x)') %用鼠标的光标定位,将sinx这个注解放在你鼠标点击的地方
legend('sinx','cosx') %添加图例
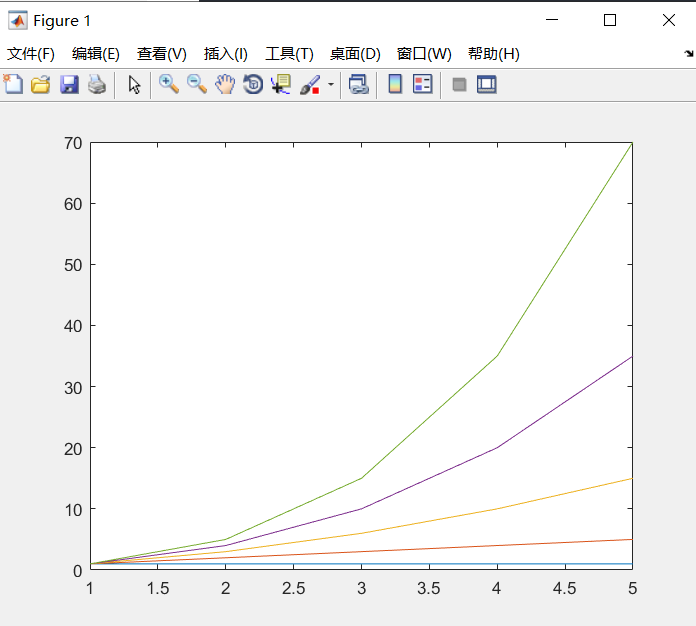
- 利用plot函数可以直接将矩阵的数据绘制在图形窗体中,此时plot函数将矩阵的每一列数据作为一条曲线绘制在窗体中。
A=pascal(5)
plot(A)
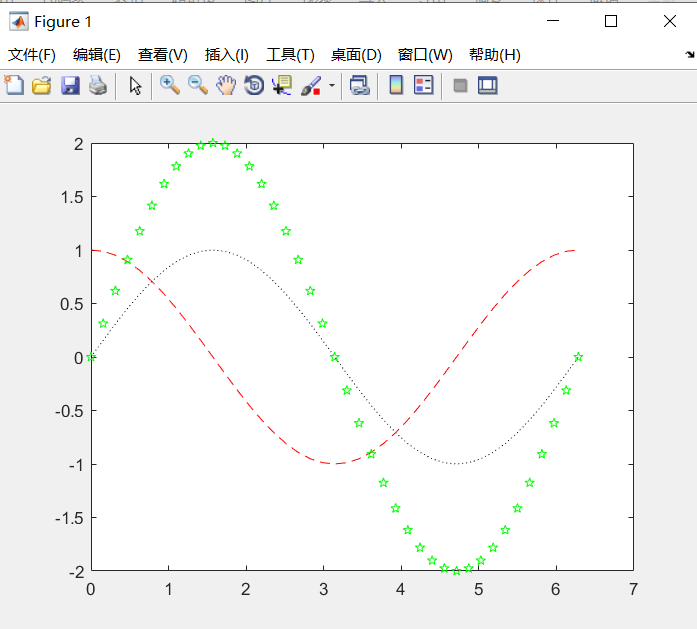
- 含选项的plot()函数
Matlab提供了一些绘图选项,用于确定所绘曲线的线型、颜色和数据点标记符号。这些选项如下表所示:
| 线型 | 颜色 | 标记符号 |
|---|
| - 实线 | b蓝色 | .点 | s 方块 |
|---|---|---|---|
| : 虚线 | g绿色 | o 圆圈 | d菱形 |
| -. 点划线 | r红色 | × 叉号 | ∨朝下三角符号 |
| – 双划线 | y黄色 | + 加号 | ∧朝上三角符号 |
| c 青色 | * 星号 | <朝左三角符号 | |
| m品红 | >朝右三角符号 | ||
| k黑色 | p五角星 | ||
| w白色 | h六角星 |
x=0:pi/20:2*pi; %x的区间是0-2*pi,pi/20是步长
y1=sin(x);
y2=cos(x);
y3=2*sin(x);
plot(x,y1,'k:',x,y2,'r--',x,y3,'gp')
- 双纵坐标函数plotyy
如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy函数,它能把具有不同量纲,不同数量级的两个函数绘制在同一个坐标中,有利于图形数据的对比分析。使用格式为:plotyy(x1,y1,x2,y2)。 - 图形保持
一般情况下,每执行一次绘图命令,就刷新一次当前图形窗口,图形窗口原有图形将不复存在,如果希望在已经存在的图形上再继续添加新的图形,可以使用图形保持命令hold。hold on/off 命令是刷新原有图形、保留原有图形,不带参数的hold命令在两者之间进行切换。 - 图形窗口分割
在实际应用中,经常需要在一个图形窗口中绘制若干个独立的图形,这就需要对图形窗口进行分割。分割后的图形窗口由若干个绘图区组成,每一个绘图区可以建立独立的坐标系并绘制图形。同一图形窗口下的不同图形称为子图。Matlab提供了subplot函数用来将当前窗口分割成若干个绘图区,每个区域代表一个独立的子图,也是一个独立的坐标系,可以通过subplot函数激活某一区,该区为活动区,所发出的绘图命令都是作用于该活动区域。调用格式:
subplot(m,n,p)
该函数把当前窗口分成m×n个绘图区,m行,每行n个绘图区,区号按行优先编号。其中第p个区为当前活动区。每一个绘图区允许以不同的坐标系单独绘制图形。 - 坐标控制
在绘制图形时,Matlab可以自动根据要绘制曲线数据的范围选择合适的坐标刻度,使得曲线能够尽可能清晰的显示出来。所以,一般情况下用户不必选择坐标轴的刻度范围。但是,如果用户对坐标不满意,可以利用axis函数对其重新设定。其调用格式为
axis([xmin xmax ymin ymax zmin zmax])
如果只给出前四个参数,则按照给出的x、y轴的最小值和最大值选择坐标系范围,绘制出合适的二维曲线。如果给出了全部参数,则绘制出三维图形。
axis函数的功能丰富,其常用的用法有:
axis equal :纵横坐标轴采用等长刻度
axis square:产生正方形坐标系(默认为矩形)
axis auto:使用默认设置
axis off:取消坐标轴
axis on :显示坐标轴
fplot()
fplot()函数可以自适应地对函数进行采样,能更好地反应函数的变化规律。
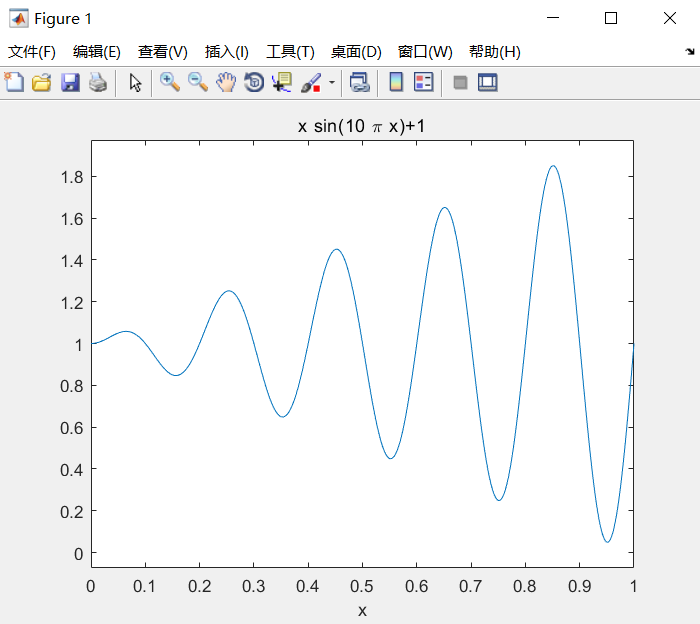
f='x*sin(10*pi*x)+1' %或者 f='x.*sin(10*pi*x)+1'
fplot(f,[0,1],1e-4) % 1e-4也可以不要,图形没什么区别
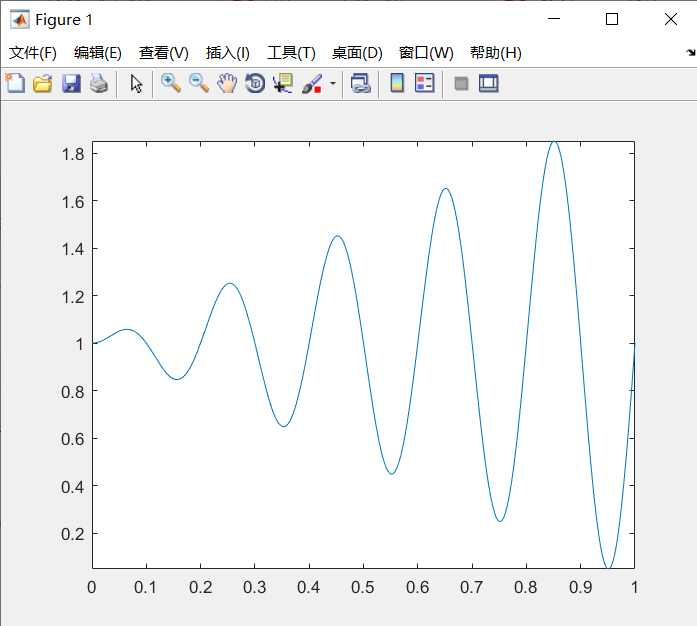
ezplot()
常用于隐函数绘图。
f='sin(x)'
ezplot(f,[0,10])
几种图形的绘制
(1)条形图
绘制条形图可以分为二维和三维条形图,其中绘制二维条形图的函数有bar(竖直条形图)和barh(水平条形图);绘制三维条形图的函数有bar3(竖直条形图)和bar3h(水平条形图)。他们的调用格式是一样的,下面只介绍bar()的用法:
1、bar(Y):若Y为向量,则分别显示每个分量的高度,横坐标从1到length(Y);若Y为矩阵,则把Y分解为行向量,分别画出,横坐标分别为从1到size(Y,1),即矩阵的行数;
2、bar(x,Y):x为指定的横坐标;
3、bar(…width):width为条形的宽度;
4、bar(…‘style’):style为指定条形的排列类型,类型有group和stack两种;
5、bar(…LineSpec):用指定的颜色LineSpec显示所有的条形。
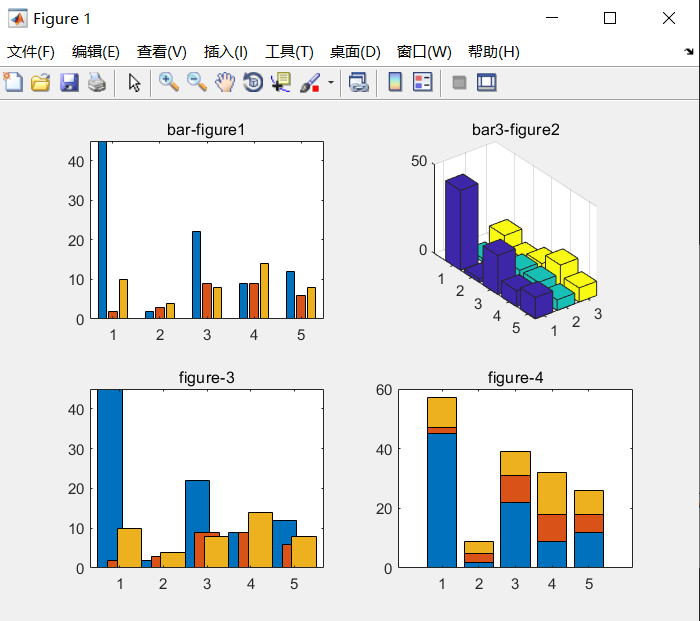
y=[45 2 10;2 3 4;22 9 8;9 9 14;12 6 8];
subplot(2,2,1);
bar(y); %普通的二维条形图
title('bar-figure1')
subplot(2,2,2);
bar3(y); %三维条形图
title('bar3-figure2')
subplot(2,2,3);
bar(y,2.5) %指定条形的宽度
title('figure-3')
subplot(2,2,4);
bar(y,'stack') %以stack的排列类型显示条形
title('figure-4')
(2)面积图
在MATLAB中,绘制面积图的函数是area()。
area(x) :与plot(x)命令一样,但是将所得曲线下方的区域填充颜色;
area(x,y):其中y为向量,与plot(x,y)一样,但是将所得曲线下方的区域填充颜色;
area(x,A):矩阵A的第一行对向量x绘图,然后依次是下一行与前面所有行值的和对向量x绘图,每个区域有各自的颜色;
area(…,level):将填充颜色改为由连线图到y=level的水平线之间的部分。
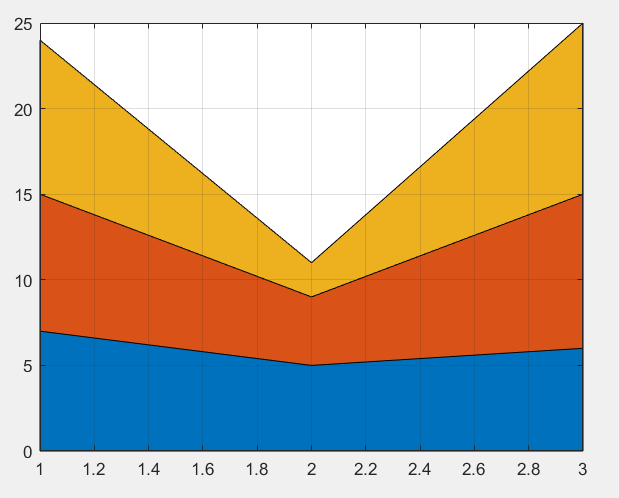
x=[1 2 3];
y=[7 8 9;5 4 2;6 9 10];
area(x,y)
grid on
set(gca,'Layer','top');
(3)饼图
饼图也分为二维和三维两种情况,二维使用pie(),三维使用pie3(),两种调用方式基本一样。
pie(X):X是向量,用X中的数据来画饼图,X中的每一个元素都是饼图的一部分,X(i)代表的饼图大小由X(i)/sum(X)来决定。若sum(X)=1,则X中元素就指定了所在部分的大小;若sum(X)<1,则画出来一个不完整的饼图。
X=[528 701 688 799];
subplot(1,2,1);
pie(X);
title('figure1')
subplot(1,2,2)
explode=[0,1,0,0]; %1是使其分割出来
pie3(X,explode);
title('figure2')
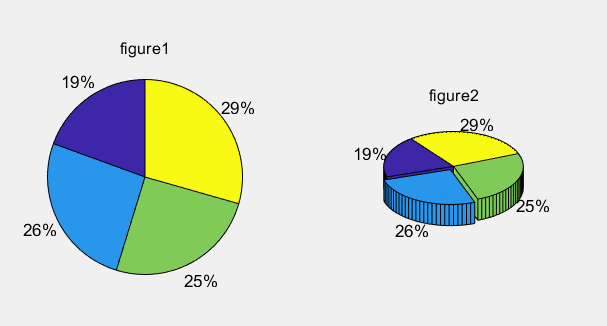
其中pie(X,explode)在实际的财务分析或者销售数据汇报时比较常用。
(4)柱状图
柱状图有两种函数:
1、hist():绘制直角坐标系下的柱状图;
用法:
n=hist(Y):把向量Y中的数据分放到等距的10个柱状图中,且返回每一个柱状图中的元素个数n;若Y为矩阵,则按列对Y进行处理。
n=hist(Y,n):n指定柱状图的数目,也就是将数据分为多少个区间,默认为10,就等同于hist(Y);
n=hist(Y,X):X为向量,把Y中元素放到m=length(X)个由X中元素指定的位置为中心的柱状图中;
[n,xout]=hist(…):返回向量n与包含频率计数与柱状图的位置向量xout,用户可以用bar(xout,n)画出条形图;
hist(…) :直接绘出柱状图。
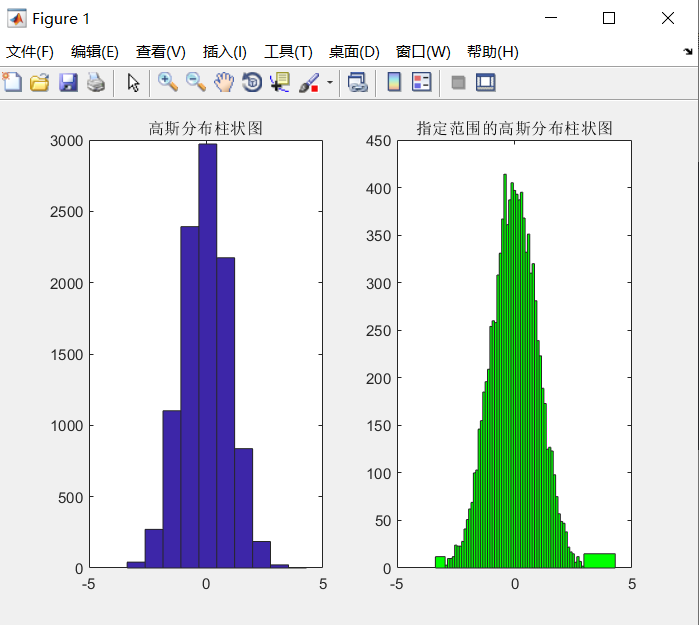
Y=randn(10000,1);%randn是均值为0方差为1的正态分布
subplot(1,2,1);
hist(Y);
title('高斯分布柱状图')
x=-3:0.1:3;
subplot(1,2,2);
hist(Y,x);
h=findobj(gca,'Type','patch');
set(h,'FaceColor','g');
title('指定范围的高斯分布柱状图')
2、rose():绘制极坐标系下的柱状图。
(5)阶梯图、杆图和填充图
阶梯图主要用在电子信息工程以及控制理论中,其调用命令为stairs
其调用格式为:
stairs(Y):用参量Y的元素画阶梯图,若Y为向量,则横坐标x的变化范围为1到length(Y),若Y为mxn矩阵,则对Y的每一行画一阶梯图,其中x的范围从1到n。
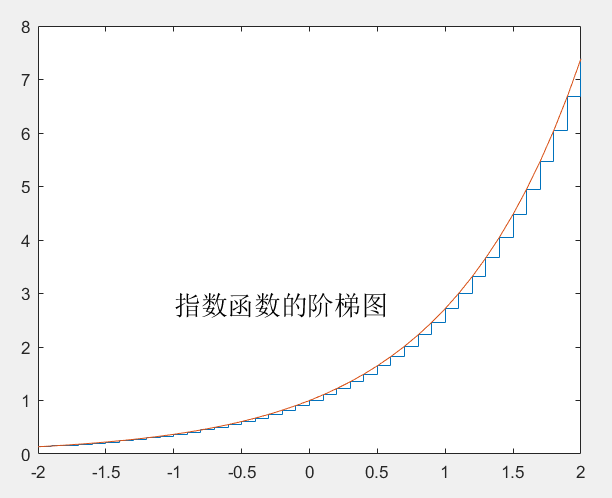
%画y=e^x的阶梯图
x=-2:0.1:2;
y=exp(x);
stairs(x,y);
hold on; %如果没有此条指令,则plot画的图形会覆盖stairs画的图形
plot(x,y)
text(-1,2.8,'指数函数的阶梯图','FontSize',16)
stairs(x,y,选项)
stem(x,y,选项)
fill(x1,y1,选项1,x2,y2,选项2,…)
前三个函数和plot的用法相似,只是没有多输入变量形式。fill函数按向量元素下标渐增次序依次用直线段连接x,y对应元素定义的数据点。
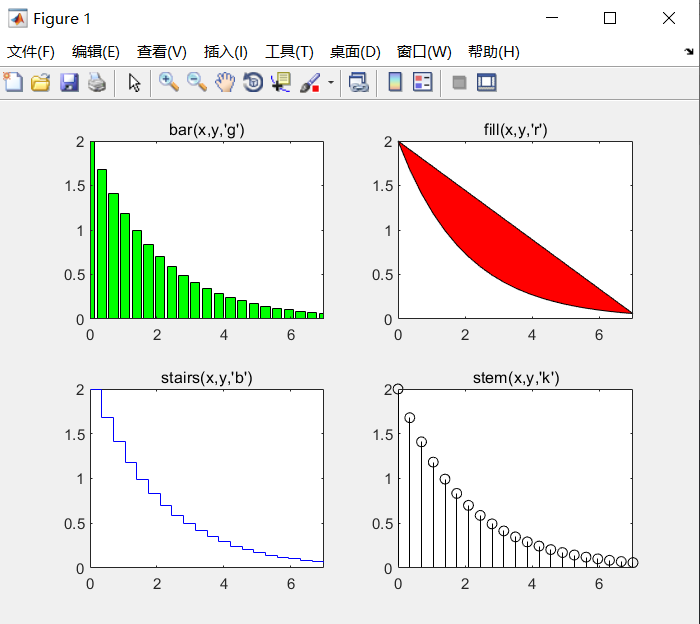
下面是包含几种图的一个例子:
x=0:0.35:7;
y=2*exp(-0.5*x);
subplot(2,2,1)
bar(x,y,'g')
title('bar(x,y,''g'')')
axis([0, 7, 0 ,2]) % axis([xmin,xmax,ymiin,ymax])是坐标系的设置函数
subplot(2,2,2)
fill(x,y,'r')
title('fill(x,y,''r'')')
axis([0, 7, 0 ,2])
subplot(2,2,3)
stairs(x,y,'b')
title('stairs(x,y,''b'')')
axis([0, 7, 0 ,2])
subplot(2,2,4)
stem(x,y,'k')
title('stem(x,y,''k'')')
axis([0, 7, 0 ,2])
(6)极坐标图
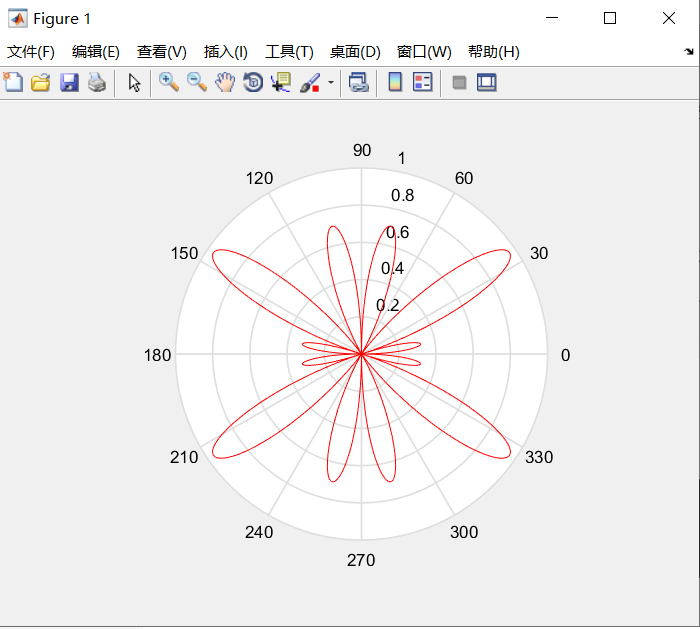
theta=0:0.01:2*pi;
rho=sin(3*theta).*cos(5*theta);
polar(theta,rho,'r')
(7)对数坐标图
semilogx(x1,y1,选项1,x2,y2,选项2…)
semilogy(x1,y1,选项1,x2,y2,选项2…)
loglog(x1,y1,选项1,x2,y2,选项2…)
这些函数中选项的定义和plot函数完全一样,所不同的是坐标轴的选取。semilogx函数使用半对数坐标,x轴为常用对数刻度,而y轴仍保持线性刻度。semilogy恰好和semilogx相反。loglog函数使用全对数坐标,x、y轴均采用对数刻度。
(8)箱线图
箱线图,又称箱型图,盒须图和盒式图,用来显示一组数据分散情况的资料。
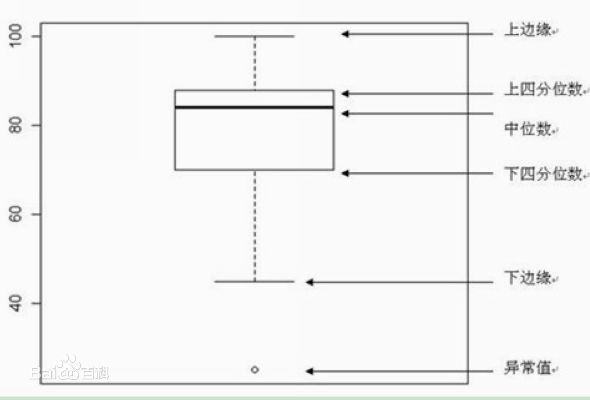
箱线图是针对连续型变量的,解题时重点关注平均水平(中位数),波动程度(箱子的上下限),异常值;
当箱子被压得很扁或者有很多异常的时候,尝试做对数变换;
当只有一个连续型变量时,不适合画箱型图,直方图更适合;
箱线图最有效的是作比较,配合一个或多个定性数据,画分组箱线图。
箱线图的详细介绍可以参照下面几篇文章:
丑图百讲 | 箱线图应该怎么用
箱线图的理解
下面是几种分析离散数据的图形:
(9)误差棒图
误差棒是以被测量的算术平均值为中点,在表示测量值方向上画的一条线段,线段长度的一半就表示不确定度,它表示被测量量以某一概率(68%或95%)落在棒上。主要用于显示不确定度。
errorbar(Y,E):画出向量Y,同时显示在向量Y中的每一元素之上的误差棒,其中误差棒为E(i)在曲线Y上面与下面的距离线段,故误差棒的长度为2E(i) ;
errorbar(X,Y,E):X、Y、E必须为同型参量。若同为向量,则画出曲线上点(X(i),Y(i))处长度为2E(i)的误差棒图;若同为矩阵,则画出曲面上点(X(i,j),Y(i,j))处带长度为E(i,j)的误差棒图;
errorbar(X,Y,L,U):X、Y、L、U必须为同型参量。若同为向量,则在点(X(i),Y(i))处画出向下长为L(i)、向上长为U(i)的误差棒图;若同为矩阵,则在点(X(i,j),Y(i,j))处画出向下长为L(i,j)、向上长为U(i,j)的误差棒图;
errorbar(…,LineSpec):画出用LineSpec指定线型、标记符、颜色等的误差棒图;
h = errorbar(…):返回线图形对象的句柄向量h。
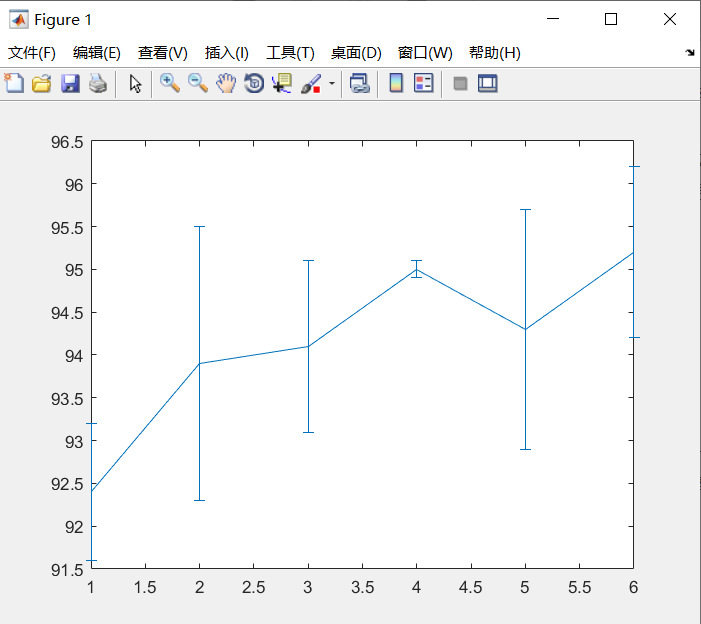
例:甲乙两个铸造厂生产同种原件,相同型号的零件尺寸,根据测量结果绘制误差棒图
x=[93.2 92.3 95.1 94.9 95.7 94.2];
y=[92.4 93.9 94.1 95.0 94.3 95.2];
e=abs(x-y);
errorbar(y,e)
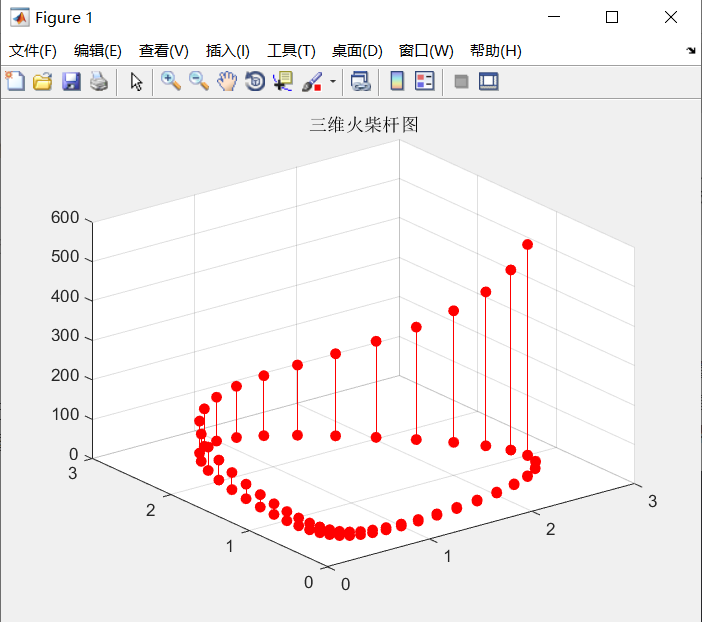
(10)火柴杆图
用线条显示数据点与x轴的距离,用以小圆圈(默认标记)或者用指定的其他标记符号与线条相连,并在y轴上标记数据点的值,这样的图像即为火柴杆图,绘制二维火柴杆图使用函数命令stem;绘制三维火柴杆图使用stem3。
t=-2*pi:pi/20:2*pi;
x=exp(cos(t));
y=exp(sin(t));
z=exp(-t);
stem3(x,y,z,'fill','r')
title('三维火柴杆图')
(11)罗盘图
罗盘图是起点是坐标原点的二维或三维向量,同时还在坐标系中显示圆形的分割线。
compass(X,Y):参量X与Y为n维向量,命令显示n个箭头,箭头的起点为原点,箭头的位置为[X(i),Y(i)];
compass(Z):参量Z为n维复数向量,命令显示n个箭头,箭头起点为原点,箭头的位置为[real(Z),imag(Z)];
compass(…,LineSpec):用参量LineSpec指定箭头图的线型、标记符号、颜色等属性;
h = compass(…):返回line对象的句柄给h。
(12)羽毛图
羽毛图是在横坐标上等距地显示向量的图形,看起来就像羽毛一样。
feather(U,V):显示由参量向量U与V确定的向量,其中U包含作为相对坐标系中的x成分,V包含作为相对坐标系中的y成分;
feather(Z):显示得数参量向量Z确定的向量,等价于feather(real(Z),imag(Z));
feather(…,LineSpec):用参量LineSpec所指定的线型、标记符号、颜色等属性画出羽毛图。
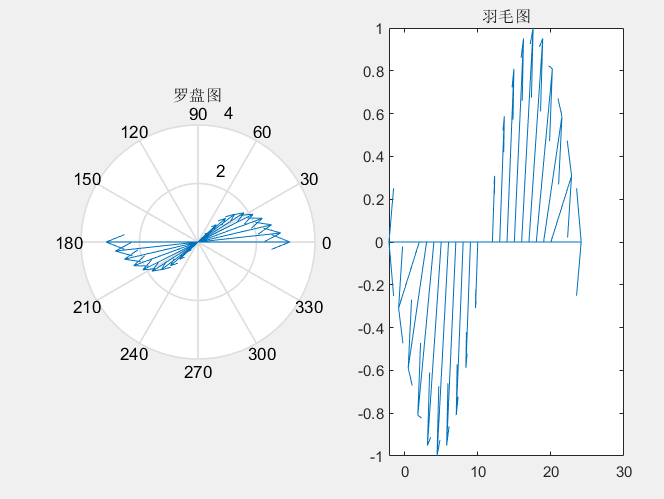
x=-pi:pi/10:pi;
y=sin(x);
subplot(1,2,1)
compass(x,y)
title('罗盘图')
subplot(1,2,2)
feather(x,y)
title('羽毛图')
(13)箭头图
上面两种也可以叫做箭头图,但是下面讲的箭头图比上面两个箭头更像数学中的向量,箭头的方向就是向量的方向,箭头的长短代表向量的大小。quiver绘制二维图形,quiver3绘制三维,它们的使用格式也十分相似,只是后者比前者多一个坐标参数。
quiver(U,V):其中U、V为m*n矩阵,绘出在范围为x = 1:n和y = 1:m的坐标系中由U和V定义的向量;
quiver(X,Y,U,V):若X为n维向量,Y为m维向量,U、V为m*n矩阵,则画出由X、Y确定的每一个点处由U和V定义的向量;
quiver(…,scale):自动对向量的长度进行处理,使之不会重叠,可以对scale进行取值,若scale=2,则向量长度伸长2倍;若scale = 0, 则如实画向量图;
quiver(…,LineSpec):用LineSpec指定的线型、符号、颜色等画向量图;
quiver(…,LineSpec,‘filled’):对用LineSpec指定的记号进行填充;
h = quiver(…):返回每个向量图的句柄。
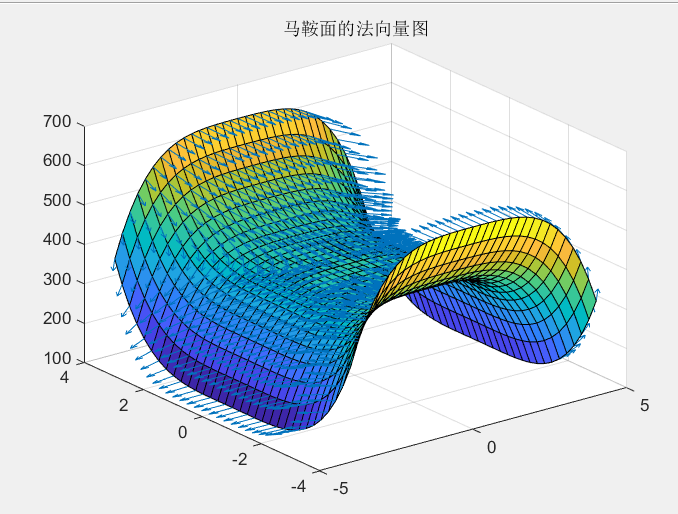
例:绘制马鞍面:z=-x4+y4-x2-y2+2xy 上的法线方向向量;
x=-4:0.25:4;
y=x;
[X,Y]=meshgrid(x,y);%将向量x和y定义的区域转换成矩阵X和Y
Z=-X.^4+Y.^4-X.^2-Y.^2+2*X*Y;
surf(X,Y,Z)
hold on
[U,V,W]=surfnorm(X,Y,Z); %计算并显示三维曲面法向量
quiver3(X,Y,Z,U,V,W,0.05)
title('马鞍面的法向量图')
暂时写到这儿吧,后续继续更新~
最后
以上就是务实小丸子最近收集整理的关于MATLAB中绘制图形绘制图形的几个函数用法几种图形的绘制的全部内容,更多相关MATLAB中绘制图形绘制图形内容请搜索靠谱客的其他文章。








发表评论 取消回复