神奇的柯西分布

今天来讲下柯西分布，它的概率密度函数如下（摘自百度百科）：

当$x_0$=0,$\gamma$=1,就得到了标准柯西分布：

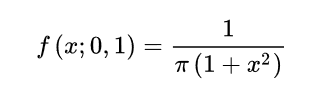
柯西分布的均值、方差都不存在，真的是很神奇。我们使用numpy对它进行抽样，具体感受下。作为对比，我使用了标准正态分布。

import numpy as np
from matplotlib import pyplot as plt
cnt=1000 #抽样1000个样本点
x=np.random.standard_cauchy(cnt)
y=np.random.randn(cnt)
plt.figure()
plt.subplot(2,1,1)
plt.hist(x,100,density=True)
plt.legend(['Cauchy'])

plt.subplot(2,1,2)
plt.hist(y,100,density=True)
plt.legend(['Gauss'])
plt.show()

结果如下：

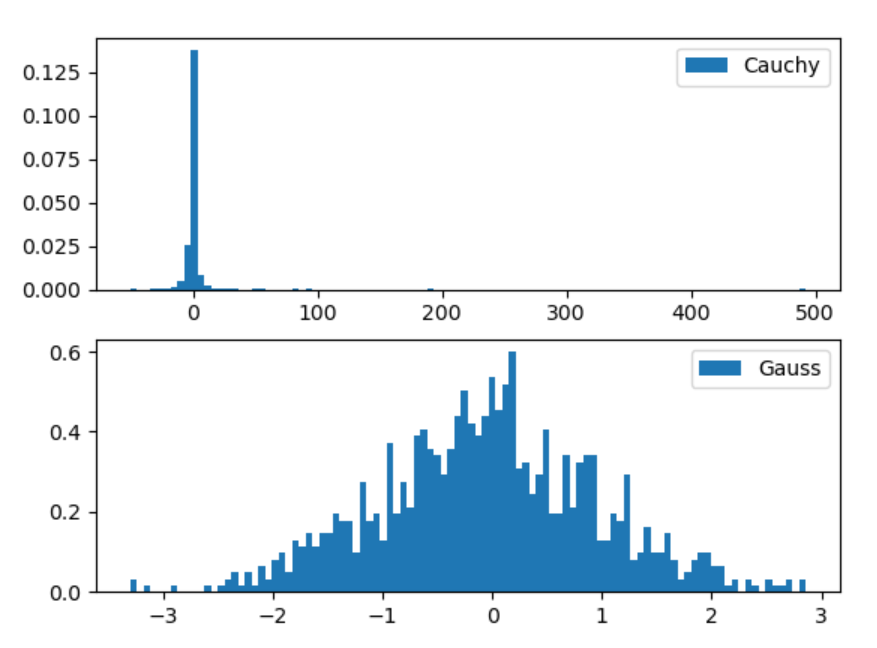
能够看出，柯西分布的取值范围非常广，很大的值也有一定概率取到，因而柯西分布也称为heavy-tail distribution。并且相比于gaussian，概率密度的最大取值只有0.1
25左右，就是x=0的那个地方。而高斯分布的取值就集中很多，0处的概率密度为0.6左右。

为了进一步验证柯西分布取值范围很大这一点，我们使用isolation forest检查一下它的异常点。

from sklearn.ensemble import IsolationForest
clf=IsolationForest(contamination=0.01,random_state=66)

#Cauchy
x=np.expand_dims(x,axis=1)
clf.fit(x)
x_pred = clf.predict(x)

#Gauss
y=np.expand_dims(y,axis=1)
clf.fit(y)
y_pred = clf.predict(y)

#打印异常点
print(x[x_pred==-1])
print(y[y_pred==-1])

柯西分布的异常点：
[[ 30.69826717]
[ 80.6436644 ]
[191.76900491]
[-33.12623108]
[ 48.05771579]
[-50.74298487]
[ 95.56422102]
[ 31.65199471]
[492.45628768]
[ 54.08139074]]

高斯分布的异常点：
[[ 2.86236466]
[-2.89916881]
[ 2.85901616]
[-3.17533096]
[ 2.69596821]
[-3.26238662]
[ 2.66074621]
[ 2.57826264]
[-3.30816191]
[ 2.73796603]]

所以，柯西分布的神奇之处就是取值分布非常宽广。这个神奇之处有什么用处呢，下回再跟大家聊~~

最后

以上就是务实小丸子为你收集整理的神奇的柯西分布的全部内容，希望文章能够帮你解决神奇的柯西分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。