一.简介
1.动态规划算法与分治法类似,其思想也是将求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
与分治法不同的是,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。
2.枚举算法的核心思想就是枚举所有的可能
二.实现
1.0-1背包问题
package com.vincent;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Main {
public static void main(String[] args) throws Exception {
//data[i][0] 表示物品重量,data[i][1] 表示商品价值
int[][] data = {{1,1500},{4,3000},{3,2000},{2,4000}};
wayOfDP(data,4);
System.out.println("--------------穷举法");
//如果对data 数据按重量从小到大排列将可以进一步优化程序,减少循环次数,该方法不需要对商品数据排序
wayOfEnum(data,new int[2],new int[]{0,4},0,new ArrayList<>());
}
/**
* 0-1背包问题动态规划算法求解:
* 定义子问题p(i,j),表示前i个商品中总重量不超过j的最大价值,w[i]表示第i个商品重量,v[i]表示第i个商品价值
* 对于第i个商品有2中选择可能
* 不选择的话背包容量不变,最优解将是p(i-1,j),选择的话背包容量减少且还可以添加p(i-1,j-v[i])
* @param data 求解问题的数据
* @param maxWeight 背包极限容量
*/
public static void wayOfDP(int[][] data,int maxWeight){
//行i表示前i个商品、列j表示重量j,组合在一起表示前i个商品对应重量的最优解
int[][] table = new int[data.length+1][maxWeight+1];
//商品组合结果,rst[i][j] 表示前i个商品背包容量j情况下是否可以装入索引为i的商品
int[][] rst = new int[data.length][maxWeight];
for(int i=1;i<=data.length;i++){//前i个商品
for(int j=1;j<=maxWeight;j++){//前j个重量
int[] item = data[i-1];
//求解前i个商品的前j个重量最优解
if(item[0] > j){
table[i][j] = table[i-1][j];
}
else{
table[i][j] = Math.max(table[i-1][j],item[1]+table[i-1][j-item[0]]);
//索引为i的商品可以装入背包
if(table[i-1][j] <= item[1]+table[i-1][j-item[0]]){
rst[i-1][j-1] = 1;
}
}
}
}
for(int i=0;i<table.length;i++){
System.out.println(Arrays.toString(table[i]));
}
System.out.println("--------------选中的对应商品");
for(int i=0;i<rst.length;i++){
System.out.println(Arrays.toString(rst[i]));
}
System.out.println("--------------选中的对应商品索引");
int weight = 0;
for(int i=data.length-1;i>=0;i--){
if(rst[i][maxWeight-1] == 1){
if(weight + data[i][0] <= maxWeight){
weight += data[i][0];
System.out.printf("%d ",i);
}
}
}
System.out.println();
}
/**
* 枚举法求解背包问题
* @param data 求解问题的数据
* @param maxValue maxValue[0]表示组合过程中的累计金额,maxValue[1]表示当前金额
* @param maxWeight maxWeight[0]表示组合过程中的重量,maxWeight[1]表示最大重量限制
* @param level 递归层级 >= 0
* @param rst 保存组合索引
*/
public static void wayOfEnum(int[][] data,int[] maxValue,int[] maxWeight,int level,List<Integer> rst){
for(int i=0;i<data.length;i++){
if(level == 0){
maxValue[1] = 0;
maxWeight[0] = 0;
rst.clear();
}
if(!rst.contains(i)) {
int weight = maxWeight[0]+data[i][0];
if(weight <= maxWeight[1]){
rst.add(i);
maxValue[1] += data[i][1];
maxWeight[0] = weight;
wayOfEnum(data,maxValue,maxWeight,level+1,rst);
}
else{
if(maxValue[1] > maxValue[0]) {
maxValue[0] = maxValue[1];
System.out.println(rst);
}
}
}
}
}
}
效果:
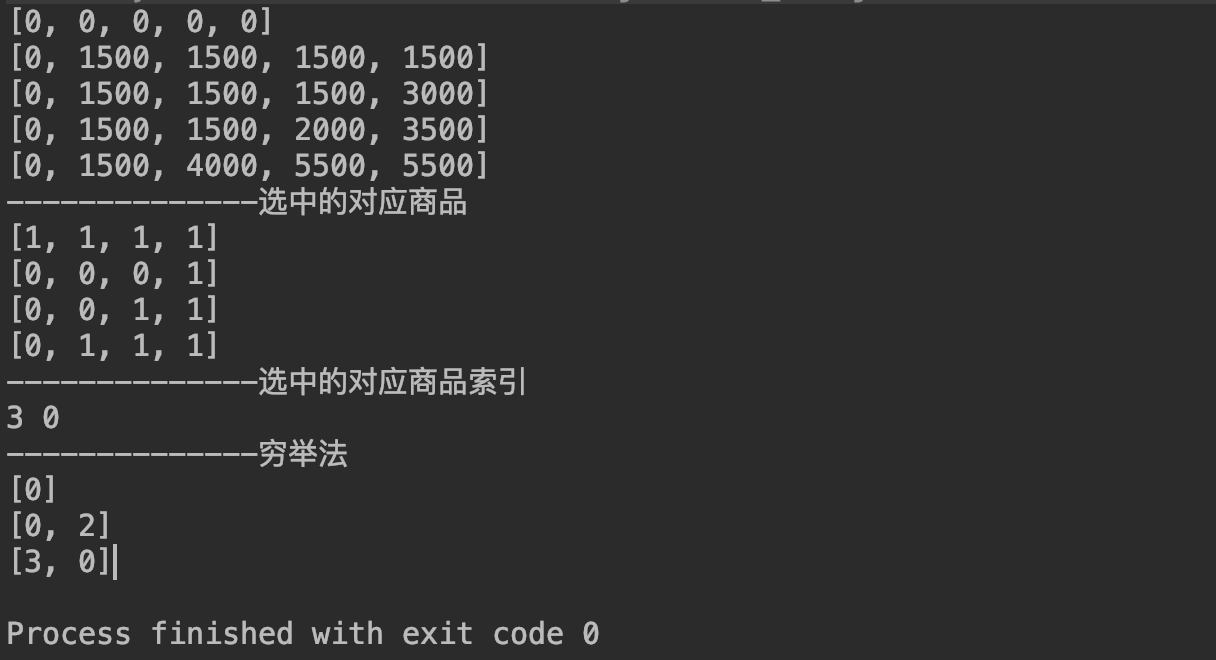
三.总结
1.动态规划对于解决多阶段决策问题的效果是明显的,但是动态规划也有一定的局限性,当变量的维数增大时,总的计算量及存贮量急剧增大
2.枚举法对于解决多维数据非常有优势,数据量太大可能导致栈溢出
最后
以上就是知性跳跳糖最近收集整理的关于动态规划 & 枚举算法的全部内容,更多相关动态规划内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复