多维高斯分布

69 阅读 0 评论 46 点赞

我是靠谱客的博主爱听歌枕头，最近开发中收集的这篇文章主要介绍多维高斯分布，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

我们常见的一维高斯分布公式为：

$mathit{N(xvert mu, sigma^2)} = frac{1}{sqrt{2pisigma^2}}exp[-frac{1}{2sigma^2}(x-mu)^2]$

拓展到高维就变成：

$mathit{N(overline{x}vert overline{mu}, Sigma)} = frac{1}{(2pi)^{frac{D}{2}}}frac{1}{|Sigma|^{frac{1}{2}}}exp[-frac{1}{2}(overline{x}-overline{mu})^{mathit{T}}Sigma^{-1}(overline{x}-overline{mu})]$

其中， $overline{x}$ 表示维度为 $mathit{D}$ 的向量， $overline{mu}$ 则是这些向量的平均值， $Sigma$ 表示所有向量 $overline{x}$ 的协方差矩阵。

本文简单探讨一下，上面这个高维的公式是怎么来的。

二维的情况

为了简单起见，本文假设所有变量都是相互独立的。即对于概率分布函数 $f(x_0,dots, x_n)$ 而言，有 $f(x_0, x_1, dots, x_n) = f(x_0)f(x_1)f(x_n)$ 成立。

现在，我们用一个二维的例子推出上面的公式。

假设有很多变量 $overline{x} = begin{bmatrix} x_1\x_2 end{bmatrix}quad$ , 他们的均值为 $overline{mu} = begin{bmatrix} mu_1\mu_2 end{bmatrix}quad$ , 方差为 $overline{sigma} = begin{bmatrix} sigma_1\sigma_2 end{bmatrix}quad$ 。

由于 $x_1$ , $x_2$ 是相互独立的，所以， $overline{x}$ 的高斯分布函数可以表示为:

$begin{flalign} f(overline{x}) & = f(x_1, x_2) & = f(x_1)f(x_2) end{flalign}$ $begin{align*} f(overline{x}) &= f(x_1,x_2)\ & = f(x_1)f(x_2)\ & = frac{1}{sqrt{2pisigma^2_1}}exp(-frac{1}{2}(frac{x_1 - mu_1}{sigma_1})^2) times frac{1}{sqrt{2pisigma^2_2}}exp(-frac{1}{2}(frac{x_2 - mu_2}{sigma_2})^2)\ & = frac{1}{(2pi)^{frac{2}{2}}(sigma_1^2sigma_1^2)^{frac{1}{2}}} exp(-frac{1}{2}[(frac{x_1 - mu_1}{sigma_1})^2 + (frac{x_2 - mu_2}{sigma_2})^2]) end{align*}$

接下来，为了推出文章前边的高维公式我们要想办法得到协方差矩阵 $Sigma$

对于二维向量 $overline{x}$ 而言，其协方差矩阵为：

$begin{align*} Sigma & = begin{bmatrix} sigma_{11} & sigma_{12} \ sigma_{21} & sigma_{22} end{bmatrix}nonumber\ & = begin{bmatrix} sigma_1^2 & sigma_{12} \ sigma_{21} & sigma_2^2 end{bmatrix} end{align*}$

由于 $x_1 , x_2$ 是相互独立的，所以 $sigma_{12} = sigma_{21} = 0 。$ 。这样， $Sigma$ 退化成 $begin{bmatrix} sigma_1^2 & 0 \ 0 & sigma_2^2 end{bmatrix}$ 。

则 $Sigma$ 的行列式 $|Sigma| = sigma_1^2 sigma_2^2$ , 带入上边 $overline{x}$ 的高斯分布函数 $f(overline{x})$ 最后化简结果中（简称公式（4））就可以得到:

$f(overline{x}) = frac{1}{(2pi)^{frac{2}{2}}|Sigma|^{frac{1}{2}}} exp(-frac{1}{2}[(frac{x_1 - mu_1}{sigma_1})^2 + (frac{x_2 - mu_2}{sigma_2})^2])$

这样一来，我们已经推出了公式的左半部分，下面，开始处理右面的 $exp$ 函数。

原始的高维高斯函数的 $exp$ 函数为： $exp[-frac{1}{2}(overline{x}-overline{mu})^{mathit{T}}Sigma^{-1}(overline{x}-overline{mu})]$ , 根据前面计算出来的 $Sigma$ ，我们可以求出它的逆：

$Sigma^{-1} = frac{1}{sigma_1^2sigma_2^2} begin{bmatrix} sigma_2^2 & 0 \ 0 & sigma_1^2 end{bmatrix}$ 。

接下来根据这个二维的例子，将原始的 $exp()$ 展开：

$begin{align*} exp[-frac{1}{2}(overline{x}-overline{mu})^{mathit{T}}Sigma^{-1}(overline{x}-overline{mu})] & = exp[-frac{1}{2}[x_1 - mu_1 quad x_2-mu_2]frac{1}{sigma_1^2sigma_2^2}begin{bmatrix} sigma_2^2&0\0&sigma_1^2 end{bmatrix}begin{bmatrix} x_1-mu_1\x_2-mu_2 end{bmatrix}]\ & = exp[-frac{1}{2}[x_1 - mu_1 quad x_2-mu_2]frac{1}{sigma_1^2sigma_2^2}begin{bmatrix} sigma_2^2(x_1-mu_1)\sigma_1^2(x_2-mu_2) end{bmatrix}]\ & = exp[-frac{1}{2sigma_1^2sigma_2^2}[sigma_2^2(x_1-mu_1)^2+sigma_1^2(x_2-mu_2)^2]]\ & = exp[-frac{1}{2}[frac{(x_1-mu_1)^2}{sigma_1^2}+frac{(x_2-mu_2)^2}{sigma_2^2}]] end{align*}$

展开到最后，发现推出了公式（4）。说明原公式 $mathit{N(overline{x}vert overline{mu}, Sigma)} = frac{1}{(2pi)^{frac{D}{2}}}frac{1}{|Sigma|^{frac{1}{2}}}exp[-frac{1}{2}(overline{x}-overline{mu})^{mathit{T}}Sigma^{-1}(overline{x}-overline{mu})]$ 是成立的。你也可以将上面的过程逆着推回去，一样可以从例子中的公式（4）推出多维高斯公式。

函数图像

知道多维的公式后，下面再简单比较一下一维和二维的图像区别。

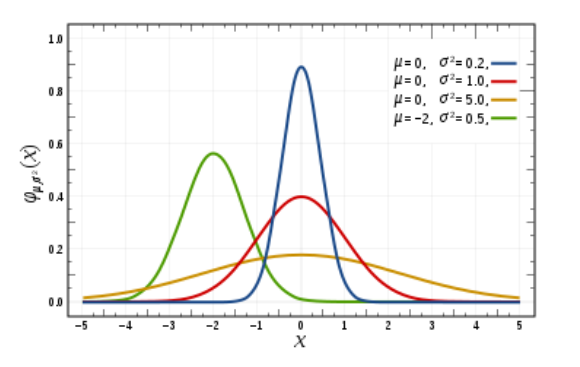
上面展示的是4个一维高斯函数的图像。高斯函数是一个对称的山峰状，山峰的中心是均值 $mu$ ，山峰的 [胖瘦] 由标准差 $sigma$ 决定，如果 $sigma$ 越大，证明数据分布越广，那么山峰越 [矮胖] ，反之，则数据分布比较集中，因此很大比例的数据集中在均值附近，山峰越[瘦高] 。在偏离均值 $mu$ 三个 $sigma$ 的范围外，数据出现的概率几乎接近0，因此这一部分的函数图像几乎与 $x$ 轴重合。

下面看二维的例子：

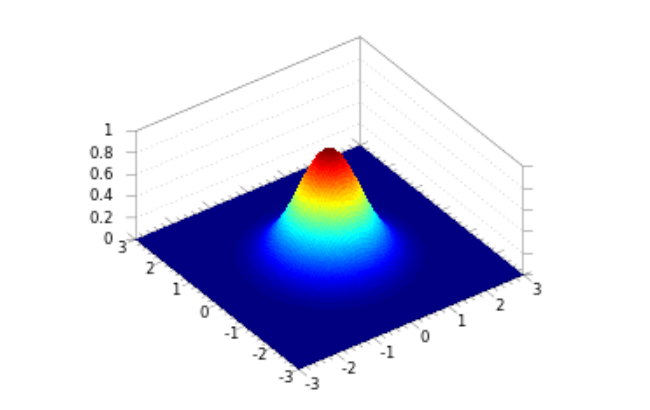
有了一维图像的例子，二维图像就可以类比出来了。如果说，一维只是山峰的一个横截面，那么二维则是一个完整的有立体感的山峰。山峰的 [中心] 和 [胖瘦] 的一维的情况是一致的，而且，对于偏离中心较远的位置，数据出现的概率几乎为0，因此，函数图像在这些地方就逐渐退化成 [平原] 了。

参数估计

另外，如果给定了很多数据点，并且知道它们服从某个高斯分布，我们要如何求出高斯分布的参数（ $mu$ 和 $Sigma$ ）呢？

当然，估计模型参数的方法有很多，最常用的就是极大似然估计。

简单起见，拿一维的高斯模型举例。假设我们有很多数据点： $(x_1,x_2,x_3,dots,x_m)$ 。一维高斯函数是：

$mathit{p(xvert mu, sigma^2)} = frac{1}{sqrt{2pi}sigma}exp(-frac{(x-mu)^2}{2sigma^2})$

首先，我们先写出似然函数：

$begin{align*} f(x_1,x_2,dots,x_m) & = prod_{i=1}^{m}frac{1}{sqrt{2pi}sigma}exp(-frac{(x_i-mu)^2}{2sigma^2}) \ & = (2pisigma^2)^{-frac{m}{2}}exp(-frac{sum_{i=1}^{n}(x_i-mu)^2}{2sigma^2}) end{align*}$

然后取对数：

$begin{align*} lnf(x_1,x_2,dots,x_m) & = -frac{m}{2}ln(2pisigma^2) - frac{1}{2sigma^2}sum_{i=1}^{n}(x_i-mu)^2 end{align*}$

求出导数，令导数为 0 得到似然方程：

$frac{partial lnf}{partial mu} = frac{1}{sigma^2}sum_{i=1}^{n}(x_i-mu) = 0$

$frac{partial lnf}{partial sigma} = -frac{m}{sigma} + frac{1}{sigma^3}sum_{i=1}^{n}(x_i-mu)^2 = 0$

我们可以求出： $mu = frac{1}{m}sum_{i=1}^{m}(x_i-mu)$ , $sigma = sqrt{frac{1}{m}sum_{i=1}^{m}(x_i - mu)^2}$ ，可以看到，这其实就是高斯函数中平均值和标准差的定义。

对于高维的情况，平均值和协方差矩阵也可以用类似的方法计算出来。

总结

本文只是从一个简单的二维例子出发，来说明多维高斯公式的来源。在 PRML 的书中，推导的过程更加全面，也复杂了许多，想深入学习多维高斯模型的还是参考教材为准。

重新对比一维和多维的公式：

$mathit{N(xvert mu, sigma^2)} = frac{1}{sqrt{2pisigma^2}}exp[-frac{1}{2sigma^2}(x-mu)^2]$

$mathit{N(overline{x}vert overline{mu}, Sigma)} = frac{1}{(2pi)^{frac{D}{2}}}frac{1}{|Sigma|^{frac{1}{2}}}exp[-frac{1}{2}(overline{x}-overline{mu})^{mathit{T}}Sigma^{-1}(overline{x}-overline{mu})]$

其实二者是等价的。一维中，我们针对的是一个数，多维时，则是针对一个个向量求分布。如果向量退化成一维，则多维公式中的 $D = 1$ , $Sigma = sigma^2$ , $Sigma^{-1} = frac{1}{sigma^2}$ , 这时多维公式就退化成一维的公式。所以，在多维的公式中，我们可以把 $Sigma$ 当作是样本向量的标准差。