前言

在数理统计和机器学习中，经常用到高斯分布，这里根据网上的资源和理解，对多维高斯分布做一个小总结。如有谬误，请联系指正。转载请注明出处。

$\nabla$ 联系方式：

e-mail: FesianXu@gmail.com

QQ: 973926198

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

微信公众号：

一维高斯分布

标准的一维高斯分布是0均值和单位方差的，数学形式如(1)：
$$p(x)=\frac{1}{\sqrt{2\pi }}exp(-\frac{x^2}{2})\text{\hspace{1em}(1)}$$
为了扩展成一般的一维高斯分布，我们引入一个线性变换$x:=A(x-\mu )$，结合(1)，有：
$$\begin{array}{rl}p(x)& =\frac{|A|}{\sqrt{2\pi }}exp(-\frac{A^2(x-\mu {)}^2}{2})\end{array}\text{\hspace{1em}(2)}$$
令$\sigma =1/A$，式(2)变为:
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}exp(-\frac{(x-\mu {)}^2}{2{\sigma }^2})\text{\hspace{1em}(3)}$$
从这里可以看出$A$和$\sigma$存在关系。在系数前乘上$|A|$是为了整个分布的积分为1。这里的$|\cdot |$表示绝对值，在多变量下，则表示行列式。

在一维高斯分布上，通过调整均值$\mu$和方差${\sigma }^2$可以调整分布的形状，使得其向左右平移，或者拉伸其"顶峰"。

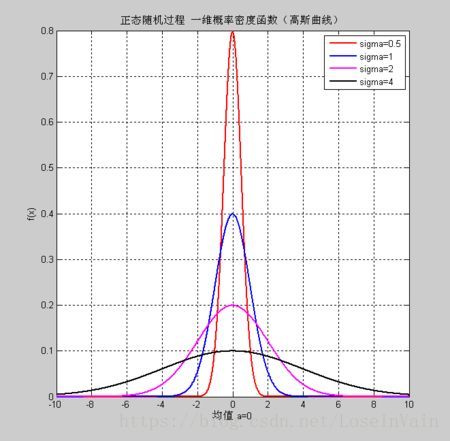
多维高斯分布

多维高斯分布其变量为$n$维变量，每个变量之间可能会存在关系，为了描述这种关系，我们引入了协方差矩阵$\Sigma$，其大小为$n\times n$，其中每一个元素为:
$$\begin{array}{rl}{\Sigma }_{i,j}& =conv(X_i,X_j)\\ & =E(X_i{X}_j)-E(X_i)E(E_j)\end{array}\text{\hspace{1em}(4)}$$

我们首先看看标准二维高斯分布的数学表达式(5)，因为是标准二维高斯分布，所以每个变量之间是独立的:
$$p(x,y)=p(x)p(y)=\frac{1}{2\pi }exp(-\frac{x^2+y^2}{2})\text{\hspace{1em}(5)}$$
为了向量化公式，用向量$\text{v}=[xy{]}^T$，有：
$$p(\text{v})=\frac{1}{2\pi }exp(-\frac{1}{2}{\text{v}}^T\text{v})\text{\hspace{1em}(6)}$$
这个时候，用$\text{v}=\text{A}(\text{x}-\mu )$，其中的$\text{A}$为$\text{v}$中每个分量的线性组合系数，也就是说$\text{A}$表示了每个变量的线性关系。有：
$$p(\text{v})=\frac{|\text{A}|}{2\pi }exp(-\frac{1}{2}(\text{x}-\mu {)}^T{\text{A}}^T\text{A}(\text{x}-\mu ))\text{\hspace{1em}(7)}$$
用$\Sigma =({\text{A}}^T\text{A}{)}^{-1}$表示其协方差，其中$|\text{A}|$为行列式，有：
$$p(\text{v})=\frac{1}{2\pi |\Sigma {|}^{1/2}}exp(-\frac{1}{2}(\text{x}-\mu {)}^T{\Sigma }^{-1}(\text{x}-\mu ))\text{\hspace{1em}(8)}$$
当维度大于2时，情形类似，$n$维的高斯分布公式为：
$$\begin{gathered} p(\text{v})=\frac{1}{(2\pi {)}^{n/2}|\Sigma {|}^{1/2}}exp(-\frac{1}{2}(\text{x}-\mu {)}^T{\Sigma }^{-1}(\text{x}-\mu )) \\ \text{v}\in {\mathbb{R}}^n\text{\hspace{1em}(9)} \end{gathered}$$

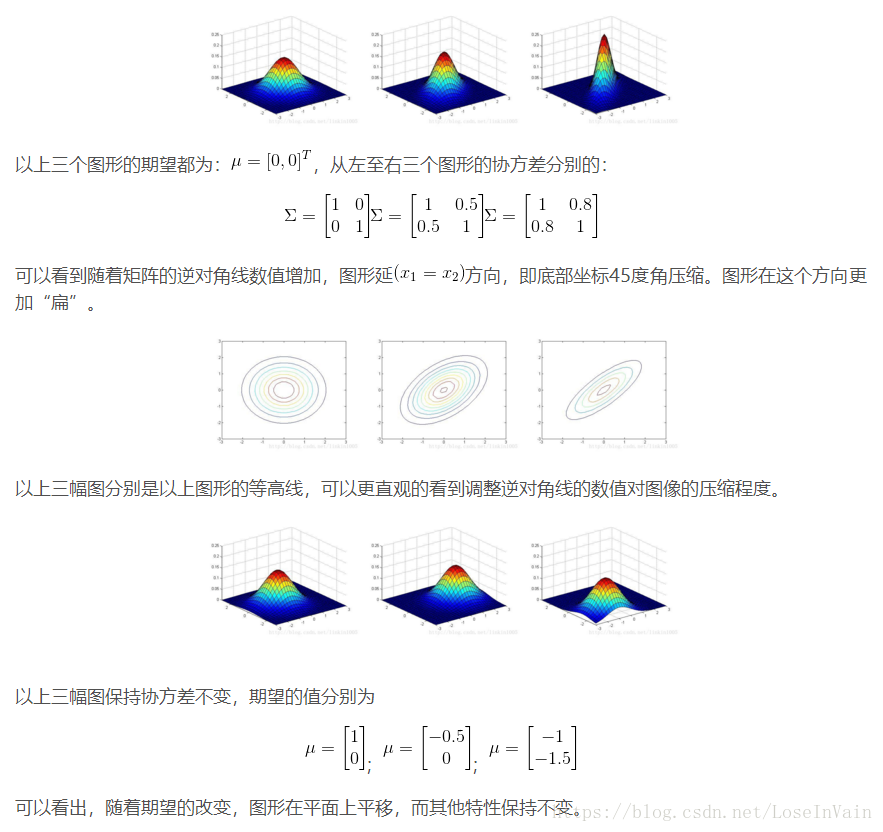
多维高斯分布的图像性质

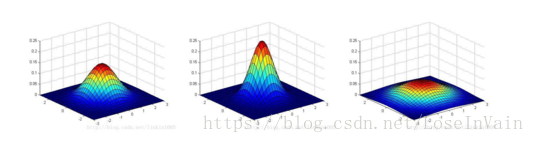
以上三个图形的期望都为：$\mu =[0,0{]}^T$，最左端图形的协方差$\Sigma =I$，中间的$\Sigma =0.6I$，最右端的$\Sigma =2I$，我们可以看出：当变小时，图像变得更加“瘦长”，而当增大时，图像变得更加“扁平”。

Reference

1. 斯坦福大学机器学习——高斯判别分析
2. 多维高斯分布是如何由一维发展而来的？

最后

以上就是洁净玉米为你收集整理的理解多维高斯分布前言一维高斯分布多维高斯分布多维高斯分布的图像性质Reference的全部内容，希望文章能够帮你解决理解多维高斯分布前言一维高斯分布多维高斯分布多维高斯分布的图像性质Reference所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。