实验一 最大最小距离法
一.实验目的
本实验的目的是使学生了解最大最小距离法聚类方法,掌握最大最小距离聚类分析法的基本原理,培养学生实际动手
和思考能力,为数据分析和处理打下牢固基础。
二. 基本思想
最大最小距离法是模式识别中一种基于试探的类聚算法,它以欧式距离为基础,取尽可能远的对象作为聚类中心。因此可以避免K-means法初值选取时可能出现的聚类种子过于临近的情况,它不仅能智能确定初试聚类种子的个数,而且提高了划分初试数据集的效率。
该算法以欧氏距离为基础,首先初始一个样本对象作为第1个聚类中心,再选择一个与第1个聚类中心最远的样本作为第2个聚类中心,然后确定其他的聚类中心,直到无新的聚类中心产生。最后将样本按最小距离原则归入最近的类。
三. 算法原理和步骤

四.最大最小距离聚类算法
该算法以欧氏距离为基础,首先辨识最远的聚类中心,然后确定其他的聚类中心,直到无新的聚类中心产生。最后将样本按最小距离原则归入最近的类。
例:样本分布如图所示。
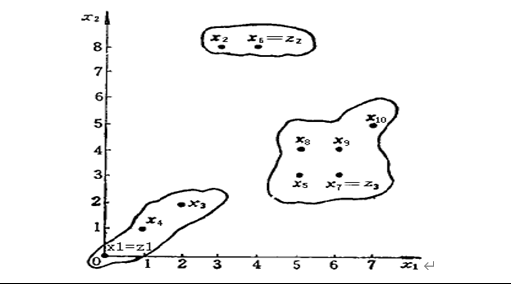
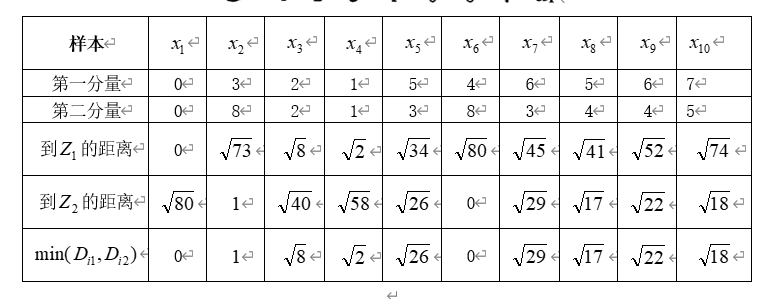


五.实验内容
见下图所示,为二维点集。
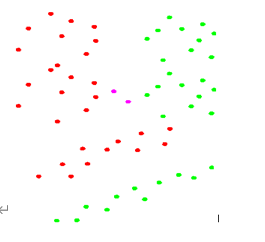
六. 测试代码
clc
close all;
x=xlsread(‘exp_1.xlsx’,‘A1:A10’);
y=xlsread(‘exp_1.xlsx’,‘B1:B10’);
figure;
plot(x,y,‘ok’,‘linewidth’,2);
grid on; axis([0 10 0 10]);
set(gca,‘xtick’,0:10);
set(gca,‘ytick’,0:10);
xlabel(‘x’); ylabel(‘y’);
max1 = 0;
max_x = 0;
max_y = 0;
T = 0.5;%阈值T由人主观设置。
for i = 1;length(x)
temp = sqrt((x(i)-x(1))^2 + (y(i)-y(1))^2);
if temp>max1
max1 = temp;
max_x = x(i);
max_y = y(i);
end
end
a_x = [];
a_y = []; minMax1 = 0;
for i = 1:length(x)
temp1 = sqrt((x(i)-x(1))^2 + (y(i)-y(1))^2);
temp2 = sqrt((x(i)-max_x)^2 + (y(i)-max_y)^2);
if minMax1<min(temp1,temp2)
minMax1 = min(temp1,temp2);
b_x = x(i);
b_y = y(i);
end
end
minMax2 = 0;
showZ1_x = [];
showZ1_y = [];
showZ2_x = [];
showZ2_y = [];
showZ3_x = [];
showZ3_y = [];
showZ4_x = [];
showZ4_y = [];
if minMax1/max1 > T
for i = 1:length(x) temp1 = sqrt((x(i)-x(1))^2 + (y(i)-y(1))^2);
temp2 = sqrt((x(i)-max_x)^2 + (y(i)-max_y)^2);
temp3 = sqrt((x(i)-b_x)^2 + (y(i)-b_y)^2);
c = min(temp1,temp2);
if minMax2<min(c,temp3) minMax2 = min(c,temp3);
b2_x = x(i); b2_y = y(i);
end
end
for i = 1:length(x)
temp1 = sqrt((x(i)-x(1))^2 + (y(i)-y(1))^2);
temp2 = sqrt((x(i)-max_x)^2 + (y(i)-max_y)^2);
temp3 = sqrt((x(i)-b_x)^2 + (y(i)-b_y)^2);
temp4 = sqrt((x(i)-b2_x)^2 + (y(i)-b2_y)^2);
if temp1<temp2 && temp1<temp3 && temp1temp2 && temp2 < temp3 && temp2< temp4
showZ2_x = [showZ2_x,x(i)];
showZ2_y = [showZ2_y,y(i)];
else if temp3 < temp1 && temp3 < temp2 && temp3 < temp4 showZ3_x = [showZ3_x,x(i)];
showZ3_y = [showZ3_y,y(i)];
else if temp4 < temp1 && temp4 < temp2 && temp4 < temp3 showZ4_x = [showZ4_x,x(i)];
showZ4_y = [showZ4_y,y(i)];
end
end
end
end
end
else if minMax1/max1 < T
for i = 1:length(x)
temp1 = sqrt((x(i)-x(1))^2 + (y(i)-y(1))^2);
temp2 = sqrt((x(i)-max_x)^2 + (y(i)-max_y)^2);
temp3 = sqrt((x(i)-b_x)^2 + (y(i)-b_y)^2);
if temp1 < temp2 && temp1 < temp3
showZ1_x = [showZ1_x,x(i)];
showZ1_y = [showZ1_y,y(i)];
else if temp1 > temp2 && temp2 < temp3
showZ2_x = [showZ2_x,x(i)];
showZ2_y = [showZ2_y,y(i)];
else if temp3 < temp1 && temp3 < temp2
showZ3_x = [showZ3_x,x(i)];
showZ3_y = [showZ3_y,y(i)];
end
end
end
end
end
end
figure
plot(showZ1_x,showZ1_y,‘or’,‘linewidth’,2);
hold on;
plot(showZ2_x,showZ2_y,‘ob’,‘linewidth’,2);
grid on;
plot(showZ3_x,showZ3_y,‘og’,‘linewidth’,2);
plot(showZ4_x,showZ4_y,‘ok’,‘linewidth’,2);
plot(x(1),y(1),‘or’,‘linewidth’,5);
plot(max_x,max_y,‘ob’,‘linewidth’,5);
plot(b_x,b_y,‘og’,‘linewidth’,5);
if minMax1/max1 > T
plot(b2_x,b2_y,‘ok’,‘linewidth’,5);
end
axis([0 10 0 10]);
set(gca,‘xtick’,0:10);
set(gca,‘ytick’,0:10);
xlabel(‘x’);
ylabel(‘y’);
title(‘最大最小距离算法’);
gtext(‘Z1’); gtext(‘Z2’); gtext(‘Z3’); gtext(‘Z4’); %顺序为:红、蓝、绿、黑
运行结果
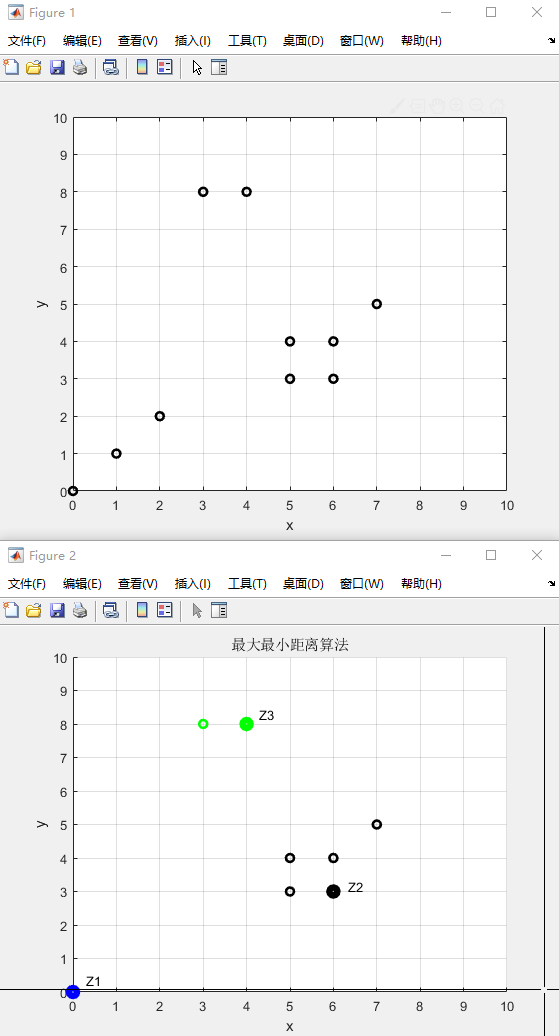
七. 分析

最后
以上就是虚拟巨人最近收集整理的关于实验一 最大最小距离法的全部内容,更多相关实验一内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。






![因子分析累计贡献率_[2018年最新整理]多元统计分析之因子分析.doc](https://www.shuijiaxian.com/files_image/reation/bcimg3.png)

发表评论 取消回复