极大似然估计
1.用途
在已知样本的情况下,估计满足样本分布的参数。
2.例子
为了调查一个学校中男生的身高分布,我们随机抽取了100个男生作为样本X = {x1,x2,…,x100};已知男生身高分布满足高斯分布,求高斯分布的参数均值和标准差。
极大似然的思想就是出现的就是最大的,可以这样想,那么多学生我们随机抽取100个,刚好就抽到我们样本中那100个学生,这说明了这100个学生是所有组合中出现概率最大的。也就是说这100个学生身高对应高斯分布中的概率密度值的乘积应该是最大的。我们把身高x对应的概率密度值记为x~p(x;θ),θ代表高斯分布。
L(θ) = p(x1;θ)*…p(x100;θ)
上式叫做似然函数,在已知样本的情况下就要保证L(θ)最大。这个式子相对于θ求导不好求,因此两端去取对数得
l(θ) = lnp(x1;θ)+…+lnp(x100;θ);
接下来就是求解l(θ)的最大值,这里θ是有两个参数的,所以要分别求偏导,令导数为零。如果有n个参数也只能一个个求偏导。 令偏导为零,然后求解最大值。
3.求解步骤
(1)写出似然函数
(2)两边取对数
(3)对新的似然函数求导
(4)令导数为零,得参数解
EM算法
1.凸函数与凹函数
凸函数:当f函数的二次导数大于等于零时,那么称f为凸函数;当其二次导大于零不等于零时,成为严格的凸函数。
凹函数:f是(严格)凹函数当且仅当-f为(严格)凸函数。
2.Jerson不等式
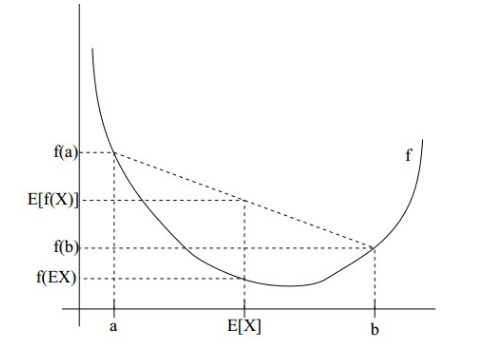
当f为凸函数时,E[f(X)]>=f(E[X]);当f为严格的凸函数时,当X为常数时,等号成立。当f为凹函数时,不等号相反。如下图:从图中可知,f(b)>f(E(X))
3.EM算法(期望最大化算法)
为了统计学校男女生的身高分布,我们随机抽样了200个身高样例X = {x1,x2,…,x200},但是不知道哪个是男生哪个是女生。如果知道男女生类别后就可以用极大似然估计了。所以这个地方就多了一个隐变量z,z服从多项式分布。对于这个地方只有男女两个类,我们就简单认为服从伯努利分布。
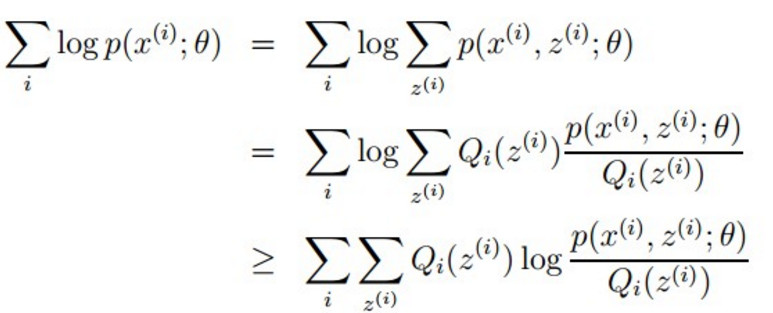
针对我们的例子来讲,i=0~200;对应不同的Zi,高斯分布参数θ也不一样。假设Zi已经知道,那么对于这200个样本同样按照极大似然的思路,求概率密度乘积的最大值。关键就是Zi是未知量,那我们只能以不等式的形式来一步步逼近真实结果了。于是,Jerson不等式就发挥作用了,为了使不等式成立,就要保证不等号左边那一部分的对数函数是凹函数,这个如何保证呢?对数函数log(x)肯定是凹函数啦。
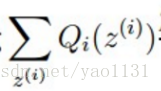 =1,之所以加入Qi主要是为了凑出平均值然后利用Jerson不等式。
=1,之所以加入Qi主要是为了凑出平均值然后利用Jerson不等式。
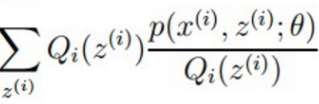 就相当于E(x)。但是这个地方的Qi是根据什么得来的,怎么算呢?前面说过了,对于Jerson不等式在凹函数的情况下,如果想取等号,那就需要变量为常数,也即
就相当于E(x)。但是这个地方的Qi是根据什么得来的,怎么算呢?前面说过了,对于Jerson不等式在凹函数的情况下,如果想取等号,那就需要变量为常数,也即
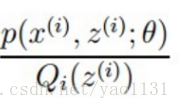 =c;由于分母的和为1,所以分子的和为c,为什么呢?举个栗子,(1+2)/(2+4) = 1/2 = 2/4。所以这个地方分子的和除以分母的和也即Qi的和结果还是c;所以由
=c;由于分母的和为1,所以分子的和为c,为什么呢?举个栗子,(1+2)/(2+4) = 1/2 = 2/4。所以这个地方分子的和除以分母的和也即Qi的和结果还是c;所以由
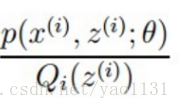 =c可以推导出
=c可以推导出
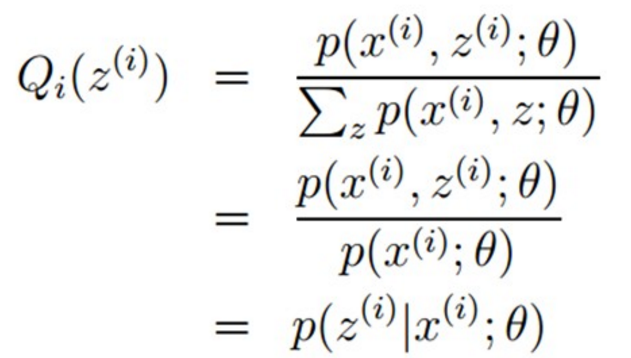
这个就是θ固定时,Qi的求解公式。 然后依据先验知识,初始化θ,这个时候
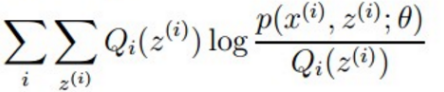 中只有Zi一个变量了,优化Zi使这个式子的结果最大也即先固定男生和女生的θ,然后对样本进行男女分类使得200个样本的概率密度乘积最大。分完后再分别以得到的男女类别里面的样本求取最大似然对应的θ’,然后再固定θ’,优化Zi,反复迭代直到收敛到最优。
中只有Zi一个变量了,优化Zi使这个式子的结果最大也即先固定男生和女生的θ,然后对样本进行男女分类使得200个样本的概率密度乘积最大。分完后再分别以得到的男女类别里面的样本求取最大似然对应的θ’,然后再固定θ’,优化Zi,反复迭代直到收敛到最优。
总结下EM算法的流程:
先初始化参数θ
1.E-STEP:根据初始化参数θ或者上一步迭代出来的参数,依据后验概率求取隐含变量的均值Qi(Zi),拉升下界。此时,
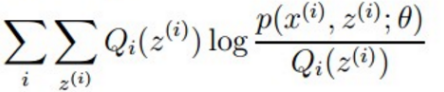 可以化简为
可以化简为
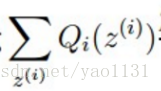 *logc
*logc
2.M-STEP:固定上一部求出来的Zi,再以求似然函数最大值为目标,更新θ。接着跳到E-STEP。
细心的读者会问,你怎么知道最终肯定会收敛的,这个就是数学上的证明了。想要详细了解,可以去网上接着搜资源继续深挖。
可以参考 高斯混合模型,一个EM算法思想的应用。
最后
以上就是专一犀牛最近收集整理的关于极大似然估计与EM算法 极大似然估计 EM算法的全部内容,更多相关极大似然估计与EM算法内容请搜索靠谱客的其他文章。








发表评论 取消回复