【读书2】【2014】基于MATLAB的雷达信号处理基础（第二版）——数据积累与相位变化建模(2)

有时必须对数据进行预处理，以确保信号分量的相位对准，从而可以实现相干积累增益。

Sometimes the data must be preprocessed toensure that the signal component phases align so that a coherent integrationgain can be achieved.

在前面的示例中，如果目标一直在运动，那么信号的测量将引入多普勒频移，则式（1.29）改写为

If the target had been moving in theprevious example, the signal component of the measurements would have exhibiteda Doppler shift, and Eq. (1.29) would instead become

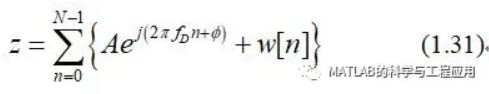
其中fD为归一化的多普勒频率。

for some value of normalized Dopplerfrequency fD.

这种情况下的信号功率将与特定的多普勒频移相关，除了非常幸运的情况，其积累的信号功率都将小于A2N2。

The signal power in this case will dependon the particular Doppler shift, but except in very fortunate cases will beless than A2N2.

然而，如果预先已知目标的多普勒频移，则在积累相加之前可以先对信号的相位变化进行补偿对齐，即：

However, if the Doppler shift is known inadvance, the phase progression of the signal component can be compensatedbefore summing:

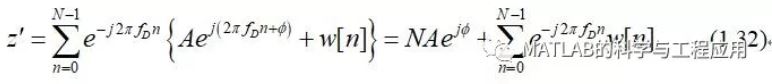
通过相位校正使得信号分量的相位对准，以便能够将信号相干叠加。

The phase correction aligns the signalcomponent phases so that they add coherently.

而噪声相位彼此之间仍然是随机的。

The noise phases are still random withrespect to one another.

Compensation for the phase progression sothat the compensated samples add in phase is an example of phase historymodeling: if the sample-to-sample pattern of target echo phases can bepredicted or estimated (at least to within a constant overall phase), the datacan be modified with a countervailing phase so that the full coherent integrationgain is achieved.（这句话有点冗余，就不翻译了。）

相位变化建模是许多雷达信号处理功能的核心，对于获得足够的信噪比增益至关重要。

Phase history modeling is central to manyradar signal processing functions and is essential for achieving adequate gainsin SNR.

在非相干积累中，相位信息被丢弃了，只对幅度、幅度平方或对数幅度进行累加。

In noncoherent integration, the phases arediscarded and some function of the magnitudes of the measured data samples areadded, such as the magnitude, magnitude-squared, or log-magnitude.

如果选择幅度平方的累加，则z为：

If the magnitude-squared is chosen, then zis formed as

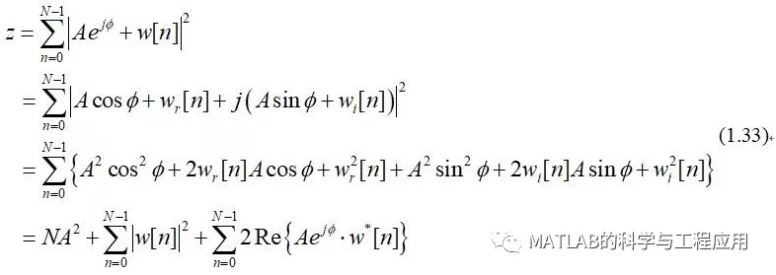
重要的事实是接收信号样本中的相位信息被丢弃。

The important fact is that phaseinformation in the received signal samples is discarded.

式（1.33）的第一行定义了非相干平方律积累。

The first line of Eq. (1.33) definesnoncoherent square-law integration.

由于非线性幅度平方运算，存在涉及信号和噪声分量之间的交叉积，z不能简单表示为信号与噪声分量之和。

The next two lines show that, because ofthe nonlinear magnitude-squared operation, z cannot be expressed as the sum ofa signal-only part and a noise-only part due to the presence of the third terminvolving cross-products between signal and noise components.

如果采用幅度或者对数幅度进行非相干积分，则存在类似的情况。

A similar situation exists if the magnitudeor log-magnitude is chosen for the noncoherent integration.

因此，与相干的情况相比，非相干积累增益的定义更加复杂。

Consequently, a noncoherent integrationgain cannot be simply defined as it was for the coherent case.

含蓄地定义非相干增益是可能的。

It is possible to define a noncoherent gainimplicitly.

——本文译自Mark A. Richards所著的《Fundamentals of Radar Signal Processing（Second edition）》

更多精彩文章请关注微信号：

最后

以上就是动人乌龟为你收集整理的【读书2】【2014】基于MATLAB的雷达信号处理基础（第二版）——数据积累与相位变化建模(2)的全部内容，希望文章能够帮你解决【读书2】【2014】基于MATLAB的雷达信号处理基础（第二版）——数据积累与相位变化建模(2)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。