在自然科学,工程技术和经济活动等各领域中,经常需要根据实验观测数据(xi,yi),i=1,2,.....,n研究因变量y与自变量x之间的关系。一般来说,变量之间的关系分为两种,一种是确定性的函数关系,另一种是不确定性关系,也称为相关关系。、
更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016
回归分析是研究变量之间的相关关系的数学工具,主要解决以下几个方面的问题。
(1)根据变量观测数据确定某些变量之间的定量关系式,即建立回归方程并估计其中的未知参数。估计参数的常用方法是最小二乘法。
(2)对求得的回归方程的可信度进行统计检验。
(3)判断自变量对因变量有无影响。特别的,在许多自变共同影响一个因变量的关系中,需要判断哪些自变量的影响是显著的,哪些自变量的影响是不显著的,将影响显著的自变量选入模型中,剔除影响不显著的变量,通常用逐步回归、向前回归和向后回归等方法。
(4)利用所求的回归方程对某一生成过程进行预测和控制。
1.MATLAB中,有三种回归模型类:LinearModel class(线性回归模型类)、NonLinear class(非线性回归模型类)和GeneralizedLinearModle class(广义线性回归),通过调用类的构造函数可以创建类对象,然后调用类对象的各种方法(例如fit和predict方法)作回归分析。
1.1线性回归模型类
1.1.1线性回归模型类的类方法
对于一元或多元线性回归,MATLAB提供了LinearModel类,用户可以根据自己的观测数据,调用LinearModel类的方法创建一个LinearModel类对象,用来求解型回归模型。LinearModel类的方法如下表所示:
| 方法名 | 功能说明 | 方法名 | 功能说明 |
| addTerms | 在线性回归模型中增加项 | plotAdjustedResponse | 绘制调整后的响应曲线 |
| anova | 对线性模型做方差分析 | plotDiagnostics | 绘制回归诊断图 |
| coefCI | 系数估计值的置信区间 | plotEffects | 绘制回归模型中每个自变量的主效应图 |
| coefTest | 对回归系数进行检验 | plotInteraction | 绘制回归模型中两个自变量的交互效应图 |
| disp | 显示线性回归分析的结果 | plotResiduals | 绘制线性回归模型的残差图 |
| dwtest | 对线性模型进行Durbin-Watson检验 | plotSlice | 绘制通过回归面的切片图 |
| feval | 利用线性回归模型进行预测 | predict | 利用线性回归模型进行预测 |
| fit | 创建线性回归模型 | random | 利用线性回归模型模拟响应的值(因变量值) |
| plot | 绘制模型拟合效果图 | removeTerms | 从线性回归模型中移出项 |
| plotAdded | 绘制指定项的拟合效果图 | step | 通过增加或移出项来改进线性回归模型 |
| stepwise | 利用逐步回归方法建立线性回归模型 |
|
|
>> mdl=LinearModel %创建一个LinearModel类对象
mdl =
Linear regression model:
y ~ 0
Coefficients:
>> methods(mdl) %查看LinearModel类中的方法
类 LinearModel 的方法:
addTerms disp plotAdded plotInteraction random
anova dwtest plotAdjustedResponse plotResiduals removeTerms
coefCI feval plotDiagnostics plotSlice step
coefTest plot plotEffects predict
1.1.2 线性回归模型类的类属性
LinearModel类对象的属性中包含了模型求解的所有结果,
>> properties(mdl) %查询LinearModel类对象mdl�
类 LinearModel 的属性:
MSE %均方误差(残差)
Robust %稳健回归参数
Residuals %残差
Fitted %拟合值
Diagnostics %回归诊断统计量
RMSE %均方根误差(残差)
Steps %逐步回归相关信息
Formula %回归模型公式
LogLikelihood %对数似然函数值
DFE %误差(残差)的自由度
SSE %误差(残差)平方和
SST %y的总离差平方和
SSR %回归平方和
CoefficientCovariance %系数统计值的协方差矩阵
CoefficientNames %
NumCoefficients
NumEstimatedCoefficients
Coefficients
Rsquared
ModelCriterion
VariableInfo
ObservationInfo
Variables
NumVariables
VariableNames
NumPredictors
PredictorNames
ResponseName
NumObservations
ObservationNames
1.2 非线性回归模型类
1.2.1 非线性回归模型类NonLinearModel类的类方法
MATLAB中提供了NonLinearModel类,用来求解一元或多元非线性回归模型类。NonLinearModel类的类方法如下表:
| 方法名 | 功能说明 |
| coefCI | 系数估计值的置信区间 |
| coefTest | 对回归系数进行检验 |
| disp | 显示非线性回归分析的结果 |
| feval | 利用非线性回归模型进行预测 |
| fit | 利用观测数据对非线性回归模型进行拟合 |
| plotDiagnositics | 绘制回归分析诊断图 |
| plotResiduals | 绘制非线性回归模型的残差图 |
| plotSlice | 绘制通过回归面的切片图 |
| predict | 利用非线性回归模型进行预测 |
| random | 利用非线性回归模型模拟响应值(因变量值) |
1.2.2非线性回归模型类NonLinearModel的类属性
NonLinearModel类对象的属性中包含了模型求解的所有结果,用户可以通过查询NonLinearModel类对象的指定属性的属性值得到想要的结果。
>> nlm=NonLinearModel
nlm =
Nonlinear regression model:
y ~ 0
Coefficients:
>> methods(nlm) %查看类方法
类 NonLinearModel 的方法:
coefCI disp plotDiagnostics plotSlice random
coefTest feval plotResiduals predict
>> properties(nlm) %查看NonLinearModel类属性
类 NonLinearModel 的属性:
MSE
Iterative
Robust
Residuals
Fitted
RMSE
Diagnostics
WeightedResiduals
Formula
LogLikelihood
DFE
SSE
SST
SSR
CoefficientCovariance
CoefficientNames
NumCoefficients
NumEstimatedCoefficients
Coefficients
Rsquared
ModelCriterion
VariableInfo
ObservationInfo
Variables
NumVariables
VariableNames
NumPredictors
PredictorNames
ResponseName
NumObservations
ObservationNames
2. 一元线性回归
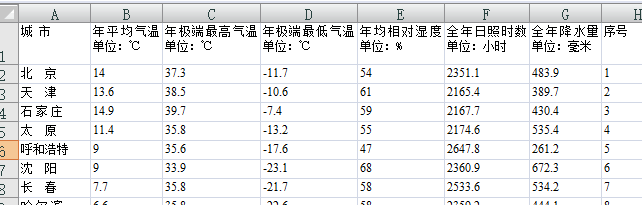
现有全国31个城市的气候情况观测数据,在“气温.xls”文件中,现在根据这些观测数据研究年平均气温和全年光照时数之间的关系。
2.1 数据的散点图
令x表示年平均气温,y表示全面日照时数。由于x和y均是一维变量,可以先从x和y的散点图上直观地观察他们之间的关系,然后再进一步的分析。
>> ClimateData = xlsread('气温.xls'); %读取数据文件
x = ClimateData(:, 1); %读取文件中的第2列,即年平均气温数据
y = ClimateData(:, 5); %读取第5列,即全年日照时数数据
figure;
plot(x, y, 'k.', 'Markersize', 15); %绘制x和y的散点图
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
R = corrcoef(x, y) %计算x和y的线性相关系数矩阵R
R =
1.0000 -0.7095
-0.7095 1.0000
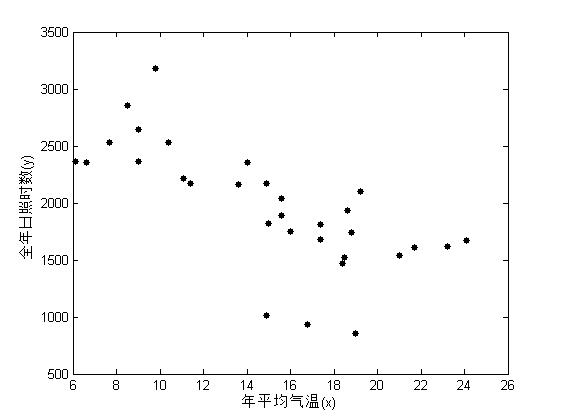
从散点图可以看出,有4组数据有些异常,除了这4组数据外,散点图编写x和y的线性趋势比较明显,可以用直线y=b0+b1*x进行拟合。
从相关系数可以看到,x和y的线性相关系数为-0.7095,表明x和y负相关。
2.2 模型的建立与求解
(1)模型的建立
建立y关于x的一元线性回归模型如下:
yi=b0+b1*x+a
a~N(0,c^2), i=1,2,...n
模型中有四个基本假定:线性假设、误差正态性假设、误差方差齐次性假定、误差独立性假定。
(2)调用LinearModel类的fit方法求解模型
mdl1 = LinearModel.fit(x,y) %模型求解
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) 3115.4 223.06 13.967 2.0861e-14
x1 -76.962 14.197 -5.4211 7.8739e-06
Number of observations: 31, Error degrees of freedom: 29
Root Mean Squared Error: 383
R-squared: 0.503, Adjusted R-Squared 0.486
F-statistic vs. constant model: 29.4, p-value = 7.87e-06
从输出的结果看,常数项b0和回归系数b1,的估计值分别为3115.4和-76.962,从而可以写出线性回归方程为
y=3115.4-76.962*x
对回归直线进行显著性检验的p=7.8739e-06<0.05,认为是y与x的线性关系是显著的。
(3)调用LinearModel类的plot方法绘制拟合效果图
下面调用LinearModel类的plot方法绘制拟合效果图。
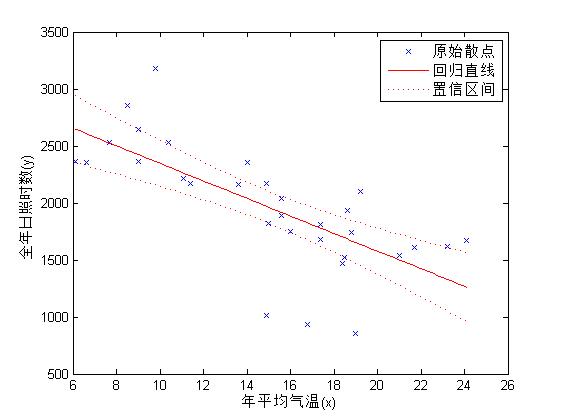
(4)预测
给定自变量x的值,可以调用LinearModel类对象的predict方法计算因变量y的预测值。例如,给定年平均气温x=5,25,计算全年日照时数y的预测值?
xnew = [5,25]'; %定义新的自变量,必须是列向量矩阵
ynew = mdl1.predict(xnew) %计算预测值
ynew =
1.0e+03 *
2.7306
1.1913
2.3 回归诊断
回归诊断主要包括以下内容:
异常点和强影响点诊断,查找数据集中的异常点(离群点)和强影响点,对模型做出改进;
残差分析,用来验证模型的基本假定,包括模型线性诊断,误差正态性诊断,误差方差齐次性诊断和误差独立性诊断
多重共线性诊断,对应多元线性回归,检验自变量之间是否存在共线性关系。
(1)查找异常点和强影响点
数据中的异常点是指远离数据中心的观测点,又称离群点,强影响点是指数据集中对回归方差参数估计结果有较大影响的观测点,通过剔除这些异常点和某些强影响点,可对模型做出改进。 LinearModel类对象的Residuals属性值中列出了标准化残差和学生化残差值,(用来查找异常点)
在回归分析中,测定值与按回归方程预测的值之差称为残差,以δ表示。残差δ遵从正态分布N(0,σ2)。(δ-残差的均值)/残差的标准差,称为标准化残差,以δ*表示。δ*遵从标准正态分布N(0,1)。实验点的标准化残差落在(-2,2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2,2)区间以外,可在95%置信度将其判为异常实验点,不参与回归直线拟合
LinearModel类对象的Diagnostics属性值中包含有杠杆值,Cook距离,Covration统计量,Dffits统计量,Dfbeta统计量等回归诊断结果,这些是用来查找强影响点的。可以调用LinearModel类对象的plotDIagnostics方法绘制个统计量对应的回归诊断图,借助回归诊断图可以直观的查找异常点和强影响点。
Res = mdl1.Residuals; %查询残差值
Res_Stu = Res.Studentized; %学生化残差
Res_Stan = Res.Standardized; %标准残差
figure;
subplot(2,3,1);
plot(Res_Stu,'kx'); %绘制学生化残差图
refline(0,-2); %在y=2和y=-2处画直线,超过这个范围即为异常点
refline(0,2);
title('(a) 学生化残差图')
xlabel('观测序号');ylabel('学生化残差');
subplot(2,3,2);
mdl1.plotDiagnostics('cookd'); %绘制Cook距离图,直线以上的点为强影响点
title('(b) Cook距离图')
xlabel('观测序号');ylabel('Cook距离');
subplot(2,3,3);
mdl1.plotDiagnostics('covratio'); %线外的为强影响点
title('(c) Covratio统计量图');
xlabel('观测序号');ylabel('Covratio统计量');
subplot(2,3,4);
plot(Res_Stan,'kx'); %绘制标准化残差图
refline(0,-2); %在y=2和y=-2处画直线,超过这个范围即为异常点
refline(0,2);
title('(d) 标准化残差图');
xlabel('观测序号');ylabel('标准化残差');
subplot(2,3,5);
mdl1.plotDiagnostics('dffits'); %绘制Dffits统计量图,超出点为强影响点
title('(e) Dffits统计量图');
xlabel('观测序号');ylabel('Dffits统计量');
subplot(2,3,6);
mdl1.plotDiagnostics('leverage'); %绘制杠杆值图,超出点为强影响点
title('(f) 杠杆值图');
xlabel('观测序号');ylabel('杠杆值');
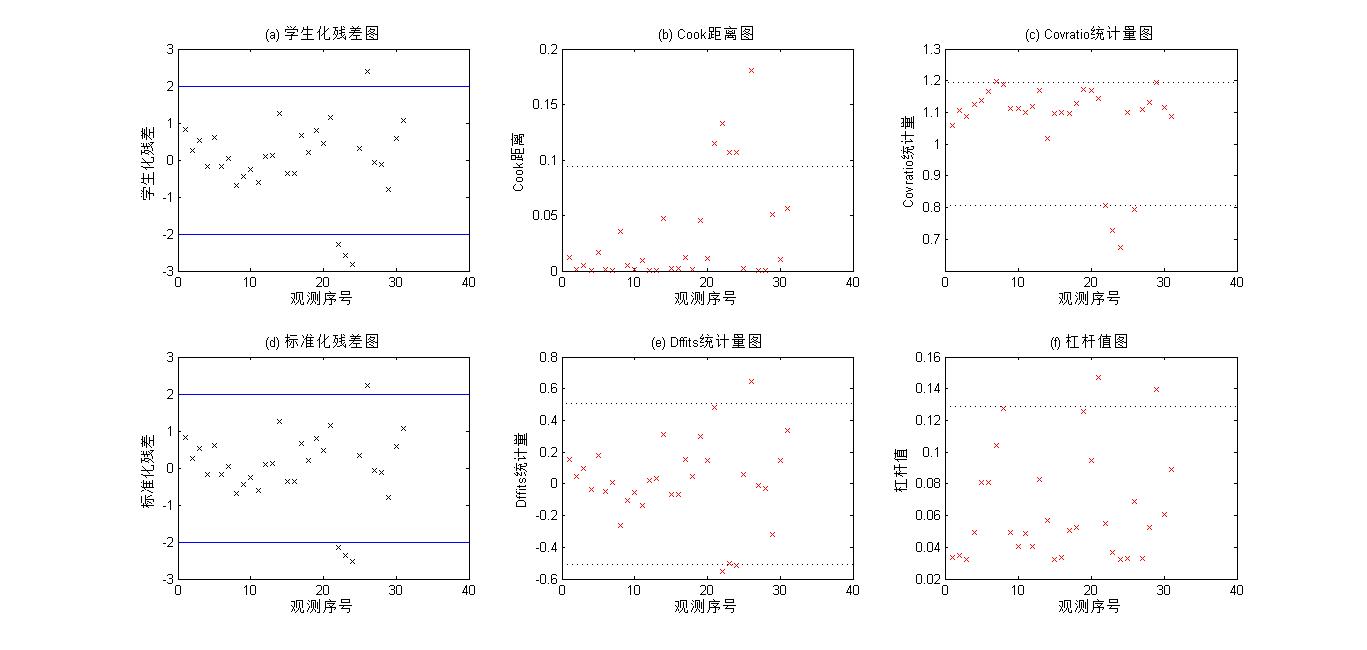
(2)模型改进
将检测到的4组异常数据剔除后重新做一元线性回归分析,对模型做出改进。
id = find(abs(Res_Stu)>2); %查找异常值的序号
mdl2 = LinearModel.fit(x,y,'Exclude',id) %去除异常值,重新求解
figure;
mdl2.plot; %绘制拟合效果图
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
title('');
legend('剔除异常数据后散点','回归直线','置信区间'); %图例
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ __________
(Intercept) 2983.8 121.29 24.601 4.8701e-19
x1 -63.628 7.7043 -8.2587 1.3088e-08
Number of observations: 27, Error degrees of freedom: 25
Root Mean Squared Error: 201
R-squared: 0.732, Adjusted R-Squared 0.721
F-statistic vs. constant model: 68.2, p-value = 1.31e-08
剔除异常值后的回归直线方程为y=2983.8-63.628*x
对回归直线进行显著性检验的p值为1.3088e-08,可知y与x的线性关系更为显著,拟合效果图如下:
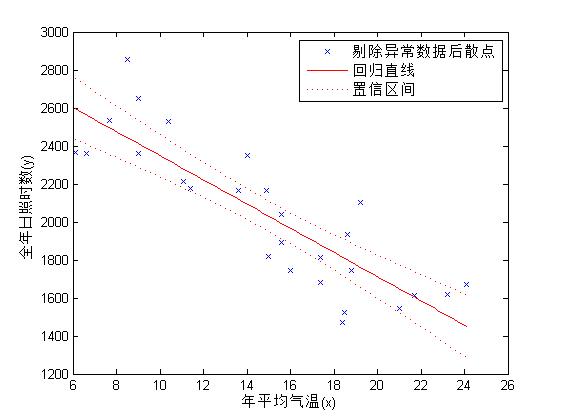
为了便于比较,做出原始数据散点、原始数据对应的回归线和剔除异常数据后的回归直线图,
figure; %新建一个图形窗口
plot(x,y,'ko'); %画出原始数据散点
hold on; %图形叠加
xnew=sort(x); %将x从小到大排序,为了画图的需要
yhat1=mdl1.predict(xnew); %计算模型1的拟合值
yhat2=mdl2.predict(xnew); %计算模型2的拟合值
plot(xnew,yhat1,'r--','linewidth',3); %画原始数据对应的回归线,红色虚线
plot(xnew,yhat2,'b','LineWidth',3); %画出剔除异常数据后的回归直线,蓝色实线
legend('原始数据散点','原始数据回归直线','剔除异常数据后回归直线'); %图例
xlabel('年平均气温');
ylabel('全年日照时数')
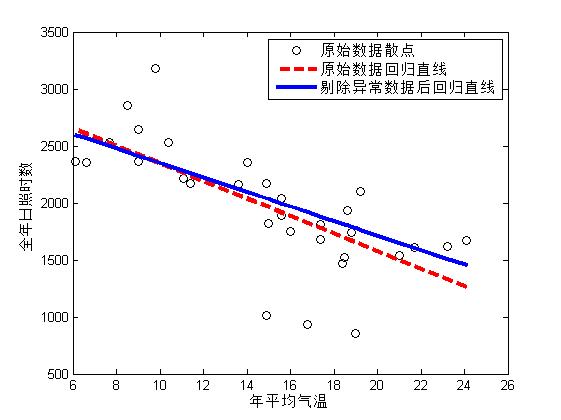
由于受异常数据的影响,两次回归结果并不相同。
(3)残差分析
在回归诊断中,常借助残差图来验证模型的基本假定是否成立。常用的残差图包括残差序列图,残差与拟合值图、残差直方图、残差正态概率图、残差与滞后残差图。可以通过调用LinearModel类对象的plotResiduals方法绘制各种残差图。
figure;
subplot(2,3,1);
mdl2.plotResiduals('caseorder'); %绘制残差值序列图
title('(a) 残差值序列图');
xlabel('观测序号');ylabel('残差');
subplot(2,3,2);
mdl2.plotResiduals('fitted'); %绘制残差与拟合值图
title('(b) 残差与拟合值图');
xlabel('拟合值');ylabel('残差');
subplot(2,3,3);
plot(x,mdl2.Residuals.Raw,'kx'); %绘制残差与自变量图
refline(0,0);
title('(c) 残差与自变量图');
xlabel('自变量值');ylabel('残差');
subplot(2,3,4);
mdl2.plotResiduals('histogram'); %绘制残差直方图
title('(d) 残差直方图');
xlabel('残差r');ylabel('f(r)');
subplot(2,3,5);
mdl2.plotResiduals('probability'); %绘制残差正态概率图
title('(e) 残差正态概率图');
xlabel('残差');ylabel('概率');
subplot(2,3,6);
mdl2.plotResiduals('lagged'); %绘制操作与滞后残差图
title('(f) 残差与滞后残差图');
xlabel('滞后残差');ylabel('残差');
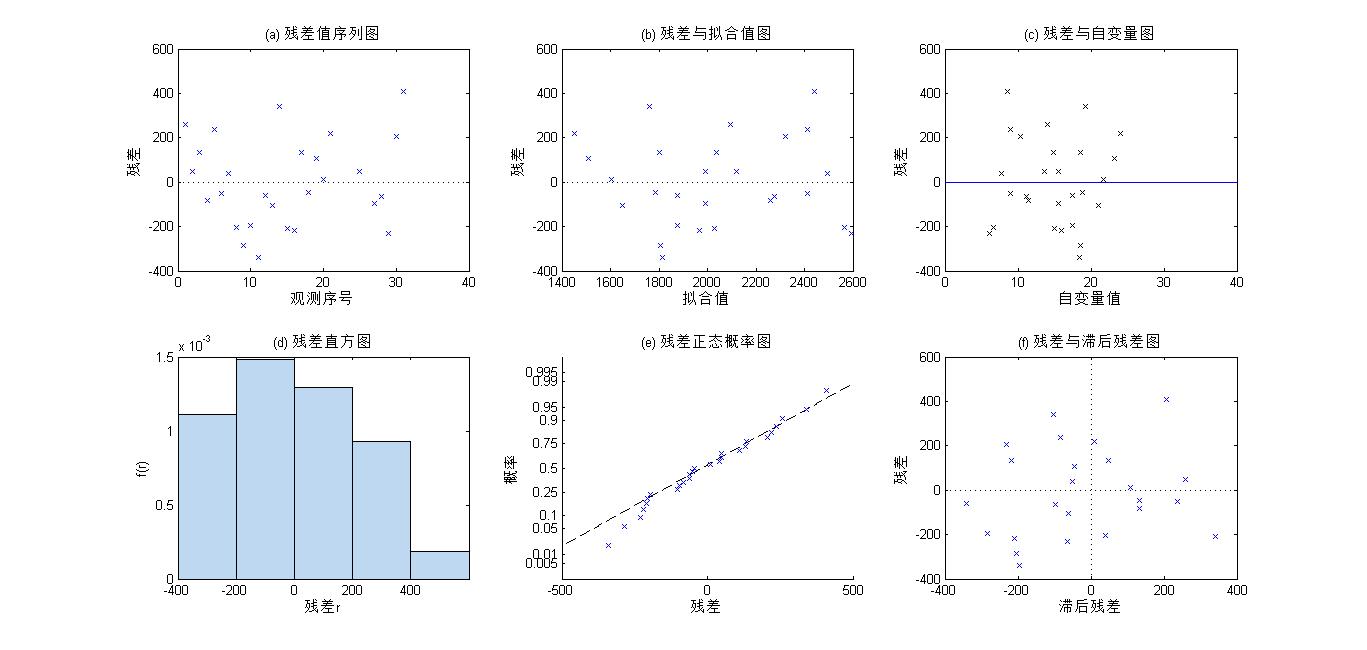
(a)残差值序列图,横坐标为观测序号,纵坐标为残差值,可以看出个观测对应的残差值随机地在水平轴y=0上下无规则地波动,说明残差值间是相互独立的。如果残差的分布有一定的规律,则说明残差间不独立。
(b)残差与拟合值图,横坐标为拟合值,纵坐标为残差值,可以看出残差基本分布在左右等宽的水平条带内,说明残差值是等方差。如果残差分布呈现喇叭口形,则说明残差不满足方差齐性假定,此时应对因变量y做某种变换(如取平方根、取对数、去倒数等),然后重新拟合。
(c)残差与自变量图,横坐标为自变量的值,纵坐标为残差值,可以看出残差基本分布在左右等宽的水平条带内,说明线性模拟与数据拟合较好。
(d)残差直方图,残差直方图反映了残差的分布。因为这里数据太少,不能根据残差直方图验证残差的正态性。
(e)残差正态概率图,用来检验残差是否服从正态分布。从图中可以看出残差基本服从正态分布
(f)残差与滞后残差图,横坐标为滞后残差,纵坐标为残差,用来检验残差间是否存在自相关性。从图中可以看出散点均匀分布在四个象限内,说明残差间不存在自相关性。
2.4 稳健回归
默认情况下,fit函数的‘RobustOpts’参数值为‘off’,此时fit函数利用普通最小二乘法估计模型中的参数,参数的估计值受异常值的影响比较大。若将fit函数的‘RobustOpt’参数值设置为‘on’,则可采用加权最小二乘法估计模型中的参数,结果受异常值的影响就比较小。
下面是稳健回归的MATLAB实现
mdl3 = LinearModel.fit(x,y,'RobustOpts','on')
mdl3 =
Linear regression model (robust fit):
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ ______ __________
(Intercept) 3034.8 182.01 16.674 2.1276e-16
x1 -68.3 11.584 -5.896 2.1194e-06
Number of observations: 31, Error degrees of freedom: 29
Root Mean Squared Error: 313
R-squared: 0.551, Adjusted R-Squared 0.535
F-statistic vs. constant model: 35.5, p-value = 1.78e-06
稳健回归得出的回归方差为y=3034.8-68.3*x。
下面对比非稳健拟合和稳健拟合,可以看出加权最小二乘拟合的稳健性。
mdl3 = LinearModel.fit(x,y,'RobustOpts','on')
xnew = sort(x); %将x从小到大排序,为了后面画图的需要
yhat1 = mdl1.predict(xnew); %计算拟合值(非稳健拟合)
yhat3 = mdl3.predict(xnew); %计算拟合值(稳健拟合)
plot(x, y, 'ko');
hold on;
plot(xnew, yhat1, 'r--','linewidth',3);
plot(xnew, yhat3, 'linewidth', 3);
legend('原始数据散点','非稳健拟合回归直线','稳健拟合回归直线');
xlabel('年平均气温(x)');
ylabel('全年日照时数(y)');
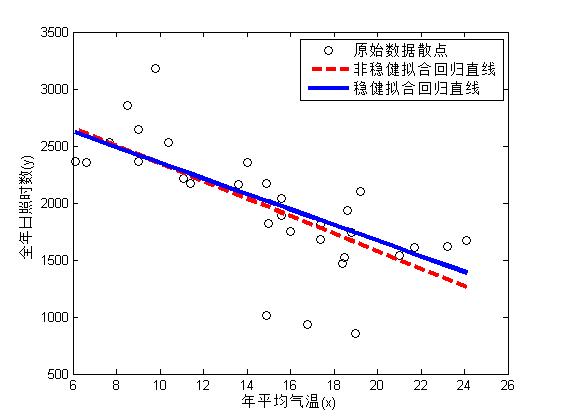
非稳健拟合是基于普通最小二乘拟合,而稳健拟合是基于加权最小二乘拟合。从图中可以看出,通过加权可以消除异常值的影响,增强拟合的文件性。
3.一元非线性回归
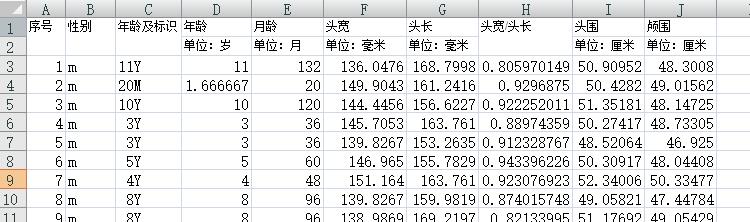
头尾是反映婴儿大脑和颅骨发育程度的的重要指标,对头围研究就有非常重要的意义。现有一组关于头围和年龄的数据,根据这些数据建立头围关于年龄的回归方程。
3.1 数据的散点图
令x表示年龄,y表示头围。x和y均为一维变量,同样可以先从x和y的散点图上直观的观察他们之间的关系,然后再做进一步分析。
HeadData = xlsread('儿童.xls'); %读入数据
x = HeadData(:, 4); %提取第4列数据,即年龄数据
y = HeadData(:, 9); %提取第9列数据,即头围数据
plot(x, y, 'k.'); %绘制x和y的散点图
xlabel('年龄(x)');
ylabel('头围(y)');
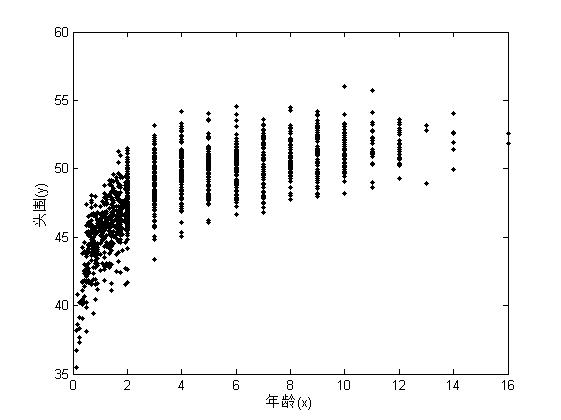
从散点图中可以看出,y(头围)和x(年龄)之间呈现非线性相关关系,应该作非线性回归方程。根据散点图的走势,可以选择负指数函数作为理论回归方程。
负指数方程的形式为 y=e(1/x),当x趋于正无穷时,y趋向于1,线急速增加,然后趋于平缓,符号散点图的趋势,但是需要加入一些参数,y=b1*e(b2/(x+b3))
3.2 模型的建立与求解
(1)模型的建立
建立y关于x的一元非线性回归模型如下:
yi=f(xi;b1,b2,b3)+ai
ai~N(0,aa^2),i=1,2,..n
式中,y=f(x,b1,b2,b3)为非线性回归方差,为上面定义的负指数函数,a为误差,服从正态分布
(2)调用NonLinearModel类的fit方法求解模型
在调用NonLinearModel类的fit方法求解模型之前, 应根据观测数据的特点选择合适的理论回归方差,这里我们选择负指数函数作为理论回归方程y=b1exp[b2/(x+b3)],但是理论回归方差往往不是唯一的,可以有多种选择.
有了理论回归方程之后,首先编写理论回归方程所对应的M函数,也可以用匿名函数的形式定义理论回归方程。函数应有两个输入参数,1个输出参数。第一个输入为未知参数向量,第2个输入为自变量观测值向量。
HeadCir = @(beta, x)beta(1)*exp(beta(2)./(x+beta(3))); %定义理论回归方差
beta0 = [53,-0.2604,0.6276]; %定义参数初始值
opt = statset; %创建统计选择的结构体
opt.Robust = 'on'; %Robust字段设为on,进行稳健拟合
nlm1 = NonLinearModel.fit(x,y,HeadCir,beta0,'Options',opt) %模型求解,稳健拟合,如果理论回归方程是由M函数定义的,需要在函数名前加@符号,即@HeadCir
nlm1 =
Nonlinear regression model (robust fit):
y ~ beta1*exp(beta2/(x + beta3))
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ __________
beta1 52.377 0.1449 361.46 0
beta2 -0.25951 0.016175 -16.044 6.4817e-53
beta3 0.76038 0.072948 10.423 1.7956e-24
Number of observations: 1281, Error degrees of freedom: 1278
Root Mean Squared Error: 1.66
R-Squared: 0.747, Adjusted R-Squared 0.747
F-statistic vs. zero model: 4.64e+05, p-value = 0
关于未知参数初始值的选择:未知参数初始值的选取是一个难点,根据散点图可以发现,随着年龄的增长,头围也在增长,但是头围不会一直增长,到了一定年龄后,头围就稳定在50-55之间,根据理论回归方差的形式,当x趋于无穷大时,y趋向于b1,所以可以选取b1的初始值为50-55之间的一个数,这里我们选取53,再注意到,初始婴儿(x=0)的头围在35左右,带入方程中,在选取一个点,x=2时,儿童的头围大约在48左右,带入方程中,就可以确定b2,和b3.
由未知参数的估计值可以写出头围关于年龄的一元非线性回归方程为
y=52.377*exp[-0.25951/(x+0.76038)]
对回归方差进行显著性检验的p=0<0.05,可知回归方程是显著的。
(3)绘制一元非线性回归曲线
xnew = linspace(0,16,50)'; %定义新的x
ynew = nlm1.predict(xnew); %求y的估计值
figure;
plot(x, y, 'k.'); %绘制原始数据的散点图
hold on;
plot(xnew, ynew, 'linewidth', 3); %绘制回归曲线
xlabel('年龄(x)');
ylabel('头围(y)');
legend('原始数据散点','非线性回归曲线');
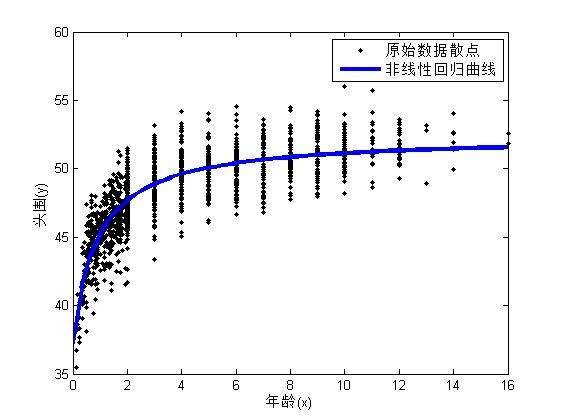
(4)参数估计值的置信区间
NonLinearModel类的coefCI方法用来计算参数估计值的置信区间
Alpha = 0.05; %定义显著性水平
ci1 = nlm1.coefCI(Alpha) %求显著性水平Alpha下的置信区间
ci1 =
52.0923 52.6609
-0.2912 -0.2278
0.6173 0.9035
(5)头围预测值和预测区间
计算给定年龄处头围预测值和预测区间
求出头围关于年龄的回归曲线后,对应给定的年龄,可以调用NonLinearModel类的predict方差求出头围的预测值、预测值的置信区间。下面调用predict函数求出y(头围)的95%的预测区间,并做出回归曲线
[yp,ypci] = nlm1.predict(xnew,'Prediction','observation');
yup = ypci(:,2); %预测区间下限
ydown = ypci(:,1); %预测区间上下限,yp是预测值
figure;
hold on;
plot(xnew,yup,'r--','LineWidth',2); %画出预测区间的上限曲线,红色曲线
plot(xnew,ydown,'b-.','LineWidth',2);%画出预测值区间的下限曲线,蓝色点画线
plot(xnew, yp, 'k','linewidth', 2); %回回归线,黑色实线
grid on;
ylim([32, 57]);
xlabel('年龄(x)');
ylabel('头围(y)');
legend('预测区间上限','预测区间下限','回归曲线','Location','SouthEast'); %图例加在右下角
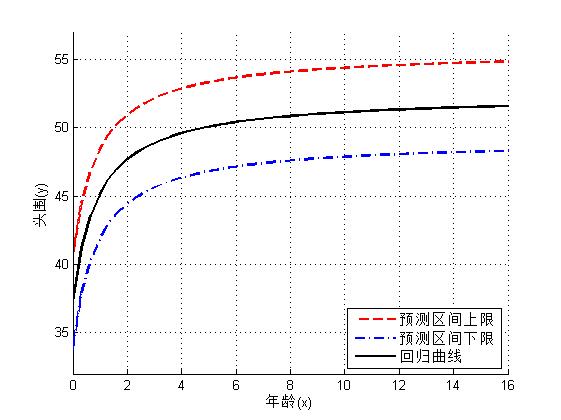
图中给出了个年龄段头围的95%的预测空间,可以用这个来评价儿童头颅发育正常与否。
3.3 回归诊断
(1)残差分析
调用NonLinearModel类的plotResiduals方法绘制残差直方图和残差正态概率图。
figure;
subplot(1,2,1);
nlm1.plotResiduals('histogram');
title('(a) 残差直方图');
xlabel('残差r');ylabel('f(r)');
subplot(1,2,2);
nlm1.plotResiduals('probability');
title('(b) 残差正态概率图');
xlabel('残差');ylabel('概率');
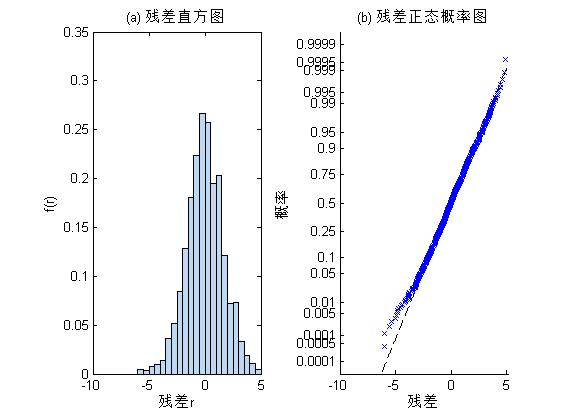
从残差直方图和残差概率图可以看出,残差分布的左尾(下尾)较长,可能存在异常值,若除去这些异常值,残差基本服从正态分布。
(2)异常值诊断
NonLinearModel类对象的Residuals属性值中列出了标准化残差和学生化残差值,下面通过学生会残差值查找异常值。
Res2 = nlm1.Residuals; %查询残差值
Res_Stu2 = Res2.Studentized; %学生化残差
id2 = find(abs(Res_Stu2)>2); %查找异常值
(3)模型改进
将检测到的异常数据剔除后重新作一元非线性回归,对模型做出改进
%剔除异常值,重新拟合
nlm2 = NonLinearModel.fit(x,y,HeadCir,beta0,'Exclude',id2,'Options',opt)
xb = x; xb(id2) = [];
yb = y; yb(id2) = [];
ynew = nlm2.predict(xnew);
figure;
plot(xb, yb, 'k.');
hold on;
plot(xnew, ynew, 'linewidth', 3);
xlabel('年龄(x)');
ylabel('头围(y)');
legend('原始数据散点','非线性回归曲线');
nlm2 =
Nonlinear regression model (robust fit):
y ~ beta1*exp(beta2/(x + beta3))
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ __________
beta1 52.369 0.12693 412.6 0
beta2 -0.26243 0.014592 -17.984 5.9309e-64
beta3 0.78167 0.067002 11.666 8.2311e-30
Number of observations: 1159, Error degrees of freedom: 1156
Root Mean Squared Error: 1.37
R-Squared: 0.807, Adjusted R-Squared 0.807
F-statistic vs. zero model: 6.11e+05, p-value = 0
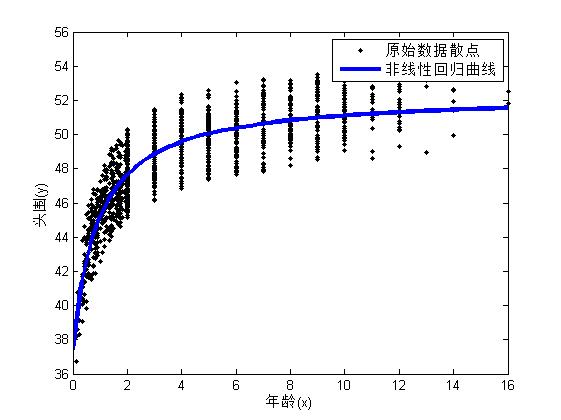
从上面的结果可知,剔除异常数据后,头围关于年龄的一元非线性回归方程为:y=52.368exp[-0.2624/(x+0.78167)]
4.多元线性和广义线性回归
在有氧锻炼中,人的耗氧能力是衡量身体状况的重要指标,它可能与一些因素有关:年龄x1,体重x2,1500米所用的时间x3,静止时心速x4,跑步后心速x5,。先对24名志愿者进行了测试,结果如下,根据测得的数据建立耗氧能力y与诸因素之间的回归模型。
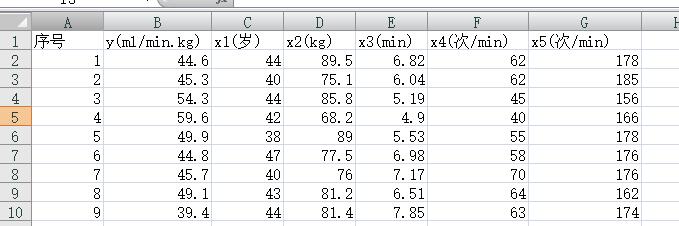
4.1 计算相关矩阵
对于多元回归,由于自变量较多,理论回归方差的选择是比较困难的,这里先计算变量间的相关系数矩阵和线性相关性检验矩阵,分析变量间的线性相关性。
data = xlsread('耗氧.xls');
X = data(:,3:7);
y = data(:,2);
[R,P] = corrcoef([y,X])
VarNames1 = {'','y','x1','x2','x3','x4','x5'};
VarNames = {'y','x1','x2','x3','x4','x5'};
newP=[VarNames1;VarNames',num2cell(P)] %转换一下格式,加入标签,便于观察
R =
1.0000 -0.3201 -0.0777 -0.8645 -0.5130 -0.4573
-0.3201 1.0000 -0.1809 0.1845 -0.1092 -0.3757
-0.0777 -0.1809 1.0000 0.1121 0.0520 0.1410
-0.8645 0.1845 0.1121 1.0000 0.6132 0.4383
-0.5130 -0.1092 0.0520 0.6132 1.0000 0.3303
-0.4573 -0.3757 0.1410 0.4383 0.3303 1.0000
P =
1.0000 0.1273 0.7181 0.0000 0.0104 0.0247
0.1273 1.0000 0.3976 0.3882 0.6116 0.0704
0.7181 0.3976 1.0000 0.6022 0.8095 0.5111
0.0000 0.3882 0.6022 1.0000 0.0014 0.0322
0.0104 0.6116 0.8095 0.0014 1.0000 0.1149
0.0247 0.0704 0.5111 0.0322 0.1149 1.0000
newP =
'' 'y' 'x1' 'x2' 'x3' 'x4' 'x5'
'y' [ 1] [0.1273] [0.7181] [5.1258e-08] [0.0104] [0.0247]
'x1' [ 0.1273] [ 1] [0.3976] [ 0.3882] [0.6116] [0.0704]
'x2' [ 0.7181] [0.3976] [ 1] [ 0.6022] [0.8095] [0.5111]
'x3' [5.1258e-08] [0.3882] [0.6022] [ 1] [0.0014] [0.0322]
'x4' [ 0.0104] [0.6116] [0.8095] [ 0.0014] [ 1] [0.1149]
'x5' [ 0.0247] [0.0704] [0.5111] [ 0.0322] [0.1149] [ 1]
从检验的p值矩阵可以看出哪些变量间的线性相关性是显著的,若p值<0.05,则认为变量间的线性相关性是显著的,反之则认为变量间的线性相关性是不显著的。从P矩阵可以看出y与x3,x4,x5的线性相关性是显著的,x3与x4,x5的线性相关性是显著的。
注意:当线性回归模型中有两个或多个自变量高度线性相关时,使用最小二乘法建立回归方程就有可能会失效,甚至会把分析引入歧途,这就是所谓的多重共线性问题。在做多元线性回归分析的时候,应做多重共线性诊断,以期得到较为合理的结果。
4.2 多元线性回归
(1)模型的建立
这里先尝试做5元线性回归,建立y关于x1,x2,....,x5的回归模型:
yi=b0+b1*xi1+b2*xi2+b3*xi3+b4*xi4+b5*xi5+a
a~N(0,aa^2), i=1,2,...,n
(2)调用LinearModel类的fit方法求解模型
调用LinearModel类的fit方法作多元线性回归,返回参数估计结果和显著性检验结果。
mmdl1 = LinearModel.fit(X,y) %5元线性回归拟合
mmdl1 =
Linear regression model:
y ~ 1 + x1 + x2 + x3 + x4 + x5
Estimated Coefficients:
Estimate SE tStat pValue
_________ ________ ________ __________
(Intercept) 121.17 17.406 6.961 1.6743e-06
x1 -0.34712 0.14353 -2.4185 0.026406
x2 -0.016719 0.087353 -0.19139 0.85036
x3 -4.2903 1.0268 -4.1784 0.00056473
x4 -0.039917 0.094237 -0.42357 0.67689
x5 -0.15866 0.078847 -2.0122 0.059407
Number of observations: 24, Error degrees of freedom: 18
Root Mean Squared Error: 2.8
R-squared: 0.816, Adjusted R-Squared 0.765
F-statistic vs. constant model: 16, p-value = 4.46e-06
根据返回值,可写出回归方程为
y=121.17-0.34713*x1-0.016719*x2-4.2903*x3-0.039917*x4-0.15866*x5
回归方差检验的p值=4.46e-6<0.05,可知在显著性水平0.05下,认为回归方差是显著的,但这并不能说明回归方程中的每一项都是显著的。参数估计表中列出了常数项和各项线性进行检验的p值,可以看出,x2,x4和x5所对应的p值大于0.05,说明在显著性水平0.05下,回归方程中的线性项x2,x4,x5都是不显著的,其中x2最不显著,其次是x4,然后x5.
(3)多重共线性诊断
多重共线性诊断的方法很多,这里用的是基于方差膨胀因子(VIF)的多重共线性诊断,
VIFi=1/(1-Ri^2) ; Ri为模型的判定系数
VIF<5时,认为不存在共线性;
5<=VIF<=10,认为存在中等程度共线性;
VIF>10,认为共线性严重,必须设法消除共线性。常用的消除共线性的方法有:去除变量,变量变换,岭回归,主成分回归
可以根据自变量的相关系数矩阵Rx计算各自变量的方差膨胀因子,自变量xi的方差膨胀因子VIFi等于Rx的逆矩阵的对角线上的第i个元素。
Rx = corrcoef(X);
VIF = diag(inv(Rx)) %inv函数求逆,diag函数求对角线上的元素
VIF =
1.5974
1.0657
2.4044
1.7686
1.6985
各自变量的方差膨胀因子均小于5,说明模型中不存在多重共线性。
(4)残差分析与异常值诊断
下面绘制残差直方图和残差正态概率图,并根据学生会残差查找异常值
figure;
subplot(1,2,1);
mmdl1.plotResiduals('histogram'); %绘制残差直方图
title('(a) 残差直方图');
xlabel('残差r');ylabel('f(r)');
subplot(1,2,2);
mmdl1.plotResiduals('probability'); %绘制残差正态该论图
title('(b) 残差正态概率图');
xlabel('残差');ylabel('概率');
Res3 = mmdl1.Residuals; %查询残差值
Res_Stu3 = Res3.Studentized; %学生化残差
id3 = find(abs(Res_Stu3)>2) %查找异常值
id3 =
10
15
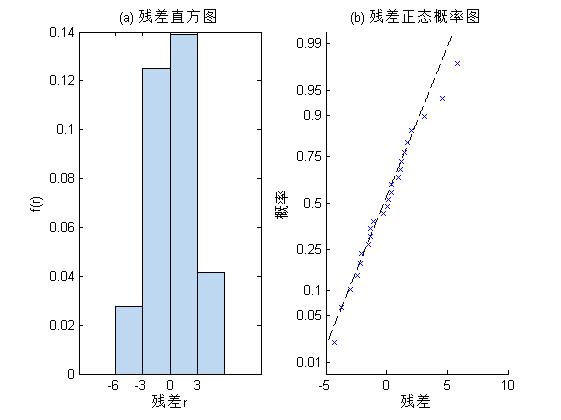
从返回结果可以看出,残差基本服从正态分布,有2组数据出现异常,它们的观测序号分别为10和15.
(5)模型改进
下面去掉异常值,并将最不显著的线性项x2,x4去掉,重新建立回归模型
y=b0+b1*xi1+b3*xi3+b5*xi5+a
a~N(0,aa^2),i=1,2,....,m
说明:在调用LinearModel类对象的fit方法作多元多项式回归时,可通过形如‘polyijk....’的参数指定多项式方差的具体形式,这里的i,j,k,.....,为取值介于0--9的整数,用来指定多项式方程中各变量的最高次数,其中,i用来指定第一个自变量的次数,j用来指定第2个自变量的次数,以此类推。
Model = 'poly10101'; %指定模型的具体形式
mmdl2 = LinearModel.fit(X,y,Model,'Exclude',id3) %去掉异常值和不显著项重新拟合
mmdl2 =
Linear regression model:
y ~ 1 + x1 + x3 + x5
Estimated Coefficients:
Estimate SE tStat pValue
________ _______ _______ __________
(Intercept) 119.5 11.81 10.118 7.4559e-09
x1 -0.36229 0.11272 -3.2141 0.0048108
x3 -4.0411 0.62858 -6.4289 4.7386e-06
x5 -0.17739 0.05977 -2.9678 0.0082426
Number of observations: 22, Error degrees of freedom: 18
Root Mean Squared Error: 2.11
R-squared: 0.862, Adjusted R-Squared 0.84
F-statistic vs. constant model: 37.6, p-value = 5.81e-08
从返回结果可以看出,剔除异常值和线性项x2,x4后的回归方程为
y=119.5-0.36229*x1-4.0411*x3-0.17739*x5
对整个回归方程进行显著性检验p=5.81e-8<0.05,说明该方程是显著的,对常数项和线性项x1,x3,x5的p值均小于0.05,说明常数项和线性项也是显著的。
4.3 多元多项式回归
虽然上面已经剔除了最不显著的线性项x2,x4,并且整个方程是显著的,但是不能认为这样的结果就是最好的回归方程,还应该尝试增加非线性项,作广义线性回归,例如二次多项式。
Model = 'poly22222'; %指定自变量x1,x2,x3,x4,x5的最高次数为2次,
mmdl3 = LinearModel.fit(X,y,Model) %完全二次多项式拟合
mmdl3 =
Linear regression model:
y ~ 1 + x1^2 + x1*x2 + x2^2 + x1*x3 + x2*x3 + x3^2 + x1*x4 + x2*x4 + x3*x4 + x4^2 + x1*x5 + x2*x5 + x3*x5 + x4*x5 + x5^2
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ ________ _________
(Intercept) 1804.1 176.67 10.211 0.0020018
x1 -26.768 3.3174 -8.069 0.0039765
x2 -16.422 1.4725 -11.153 0.0015449
x3 -7.2417 17.328 -0.41792 0.70412
x4 1.7071 1.5284 1.1169 0.34543
x5 -5.5878 1.2082 -4.6248 0.019034
x1^2 0.034031 0.02233 1.524 0.22489
x1:x2 0.18853 0.014842 12.702 0.0010526
x2^2 -0.0024412 0.0030872 -0.79075 0.48684
x1:x3 0.23808 0.21631 1.1006 0.35145
x2:x3 -0.56157 0.087918 -6.3874 0.0077704
x3^2 0.68822 0.63574 1.0826 0.35825
x1:x4 0.016786 0.015763 1.0649 0.36502
x2:x4 0.0030961 0.0058481 0.52942 0.63319
x3:x4 -0.065623 0.071279 -0.92065 0.42513
x4^2 -0.016381 0.0047701 -3.4342 0.041411
x1:x5 0.03502 0.011535 3.0359 0.056047
x2:x5 0.067888 0.0063552 10.682 0.0017537
x3:x5 0.17506 0.063871 2.7408 0.071288
x4:x5 -0.0016748 0.0056432 -0.29679 0.78599
x5^2 -0.007748 0.0027112 -2.8577 0.064697
Number of observations: 24, Error degrees of freedom: 3
Root Mean Squared Error: 0.557
R-squared: 0.999, Adjusted R-Squared 0.991
F-statistic vs. constant model: 123, p-value = 0.00104
由计算结果可知,整个回归方程显著性检验的p=0.00104<0.05,说明在显著性水平0.05下,y关于x1,x2,x3,x4,x5的完全二多项式回归方差是显著的。
上面调用fit函数分布做了5元线性回归拟合,3元线性回归拟合和完全二次多项式回归拟合得出了3个回归方程,下面绘制出这三个拟合的效果图进行对比
figure;
plot(y,'ko'); %绘制因变量y与观察序号的散点图
hold on
plot(mmdl1.predict(X),':'); %绘制5元线性回归的拟合效果图
plot(mmdl2.predict(X),'r-.'); %绘制3元线性回归的拟合效果图
plot(mmdl3.predict(X),'k'); %绘制完全二次多项式回归的拟合效果图
legend('y的原始散点','5元线性回归拟合',...
'3元线性回归拟合','完全二次回归拟合');
xlabel('y的观测序号');
ylabel('y');
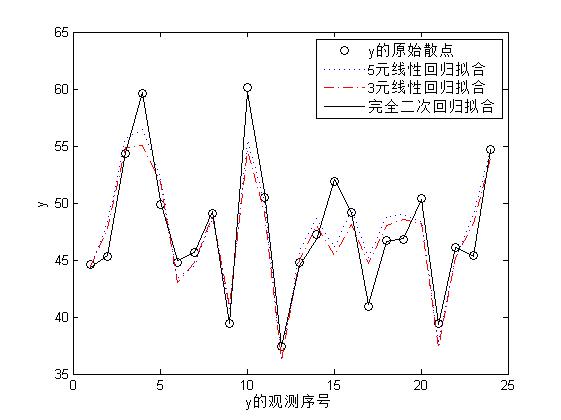
横坐标是因变量的观测序号,纵坐标是因变量的取值,从图中可以看出,完全二次多项式回归拟合的效果最好,5元和3元线性回归拟合的效果差不多。
4.4 逐步回归
逐步回归法是根据自变量对因变量y的影响大小,将他们逐个进入回归方差,影响最显著的变量先引入回归方程,在引入一个变量的同时,对已引入的自变量逐个检验,将不显著的变量再从回归方差中剔除,最不显著的变量线被剔除,直到再也不能向回归方差中引入新的变量,也不能从回归方差中剔除任何一个变量为止。这样就保证了最终得到的回归方程是最优的。
LinearModel类对象的stepwise方法用来作逐步回归,这里在二次多项式的基础上,利用逐步回归方法,建立耗氧能力y与诸多因素之间的二次多项式回归模型。
mmdl4 = LinearModel.stepwise(X,y, 'poly22222') %逐步回归
figure;
plot(y,'ko');
hold on
plot(mmdl4.predict(X),':','linewidth',2)
legend('y的原始散点','逐步回归拟合');
xlabel('y的观测序号');
ylabel('y');
mmdl4 =
Linear regression model:
y ~ 1 + x1^2 + x1*x2 + x2*x3 + x1*x4 + x4^2 + x1*x5 + x2*x5 + x3*x5 + x5^2
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ __________
(Intercept) 1916.6 106.48 17.999 2.2957e-08
x1 -29.485 1.6156 -18.251 2.0321e-08
x2 -15.841 0.92505 -17.124 3.553e-08
x3 3.3267 4.4986 0.7395 0.47845
x4 0.757 0.43986 1.721 0.11936
x5 -6.547 0.69061 -9.4801 5.5705e-06
x1^2 0.060353 0.0051667 11.681 9.6821e-07
x1:x2 0.17622 0.010126 17.403 3.0846e-08
x2:x3 -0.46789 0.050314 -9.2994 6.5277e-06
x1:x4 0.034115 0.0041517 8.2173 1.7857e-05
x4^2 -0.019258 0.0032306 -5.9612 0.00021239
x1:x5 0.045394 0.0050247 9.0342 8.2768e-06
x2:x5 0.063051 0.0043992 14.332 1.6742e-07
x3:x5 0.165 0.025546 6.4588 0.00011693
x5^2 -0.0052175 0.0016766 -3.1119 0.01248
Number of observations: 24, Error degrees of freedom: 9
Root Mean Squared Error: 0.521
R-squared: 0.997, Adjusted R-Squared 0.992
F-statistic vs. constant model: 201, p-value = 1.82e-09
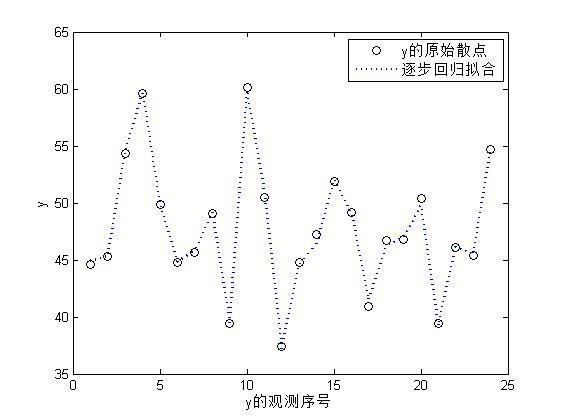
在二次多项式回归模型的基础上,进行逐步回归,得到的回归方程
y=1916.6-29.485*x1-15.841*x2.......................................
对回归方差进行显著性检验的p=1.82e-09<0.05,说明整个回归方程是显著的。
5.多项式回归
在用回归分析方法作数据拟合时,很多情况下很难写出回归函数的解析表达式,例如股票历史价格的拟合,海岸线拟合,地形曲面拟合等。此时,可借助于多项式回归,根据已知的变量观测数据,构造出一个易于计算的多项式函数来描述变量间的不确定性关系,还可以利用该函数计算非数据节点的变量近似值。
5.1 多项式回归模型
对于可控变量x和随机变量y的m(m>n)次独立的观测(xi,yi),i=1,2,....,m,若y(因变量,也称为响应变量)和x(自变量)之间的回归模型为:
yi=p1*xi^n+p2*xi^n-1+....+pn*xi+pn+1 +a
a~N(o,aa^2), i=1,2,....m
其中p1,p2,.....,pn+1为未知参数,yi为回归多项式模型
5.2 多项式回归的MATLAB实现
(1)polyfit函数的用法
MATLAB中提供了polyfit函数,用来做多项式曲线拟合,求解yi=p1*xi^n+p2*xi^n-1+....+pn*xi+pn+1 +a中的未知参数,polyfit函数的调用格式如下:
<1>p=polyfit(x,y,n)
返回n次(阶)多项式回归方程中系数向量的估计值p,这里的p是一个1x(n+1)的行向量,按降幂排列。输入参数x为自变量观测值向量,y为因变量观测值向量,n为正整数,用来指定多项式的阶数。
<2>[p,s]=polyfit(x,y,n)
还返回一个结构体变量s,可作为polyval函数的输入,用来计算预测值及误差的估计值。s有一个normr字段,字段值为残差的模,其值越小,表示拟合越精确。
<3>[p,s,mu]=polyfit(x,y,n)
首先对自变量x进行标准化变换,x=(x-u)/a ;这里u为x的均值,a为x的标准差,然后对y和标准化变换后的x作多项式回归,返回系数向量的估计值p,结构体变量s,已及mu=[u,a]
(2)polyval函数的用法
MATLAB提供了polyval函数,用来根据多项式系数向量计算多项式的值,调用格式如下:
<1>y=polyval(p,x)
计算n次多项式y=p1*x^n+....+pn*x+pn+1在x处的值,输入参数p=[p1,p2,.....,pn]为系数向量,按降幂排列,x为用户指定的自变量取值向量。输出参数y是与x等长的向量。
<2>[y,delta]=polyval(p,x.s)
根据polyfit函数返回的系数向量p和结构体s计算因变量y的预测值,已经误差的标准差的估计值delta。若误差相互独立,服从同方差的正态分布,则[y-delta,y+delta]可作为预测值的50%置信区间。
<3>y=polyval(p,x,[ ],mu) 或[y,delta]=polyval(p,x,s,mu)
首先对自变量x进行标准化变换,然后进行相应的计算,输入参数mu是polyfit函数的第3个输出参数。
(3)poly2sym函数的用法
MATLAB中提供了poly2sym函数,用来把多项式系数向量转为符号多项式,调用格式如下:
<1> r=poly2sym(p)
根据多项式系数向量p生成多形式的符号表达式r。输入参数p是按降幂排列的多项式系数向量
5.3 多项式回归示例
现有我国2007年1月到2011年11月的食品价格分类指数数据,如下,根据这些数据研究全国食品零售价格分类指数(上年同月=100)和时间的关系。
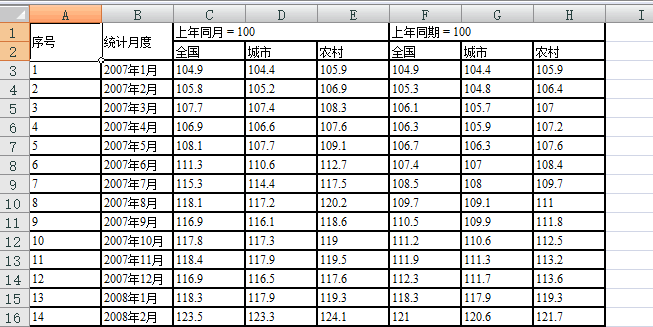
(1)数据的散点图
用序号表示时间,记为x,用y表示全国食品零售价格分类指数(上年同月=100)。由于x和y均为一维变量,可以先从x和y的散点图上直观地观察他们之间的关系,然后在做进一步的分析。
[Data,Textdata] = xlsread('食品价格.xls'); %读取数据
x = Data(:,1); %提取Data中的第一列,即观测序号
y = Data(:,3); %提取Data中第3列,即价格指数数据
figure;
plot(x,y,'k.','Markersize',15); %绘制x,y的散点图
xlabel('时间序号');
ylabel('食品零售价格分类指数');
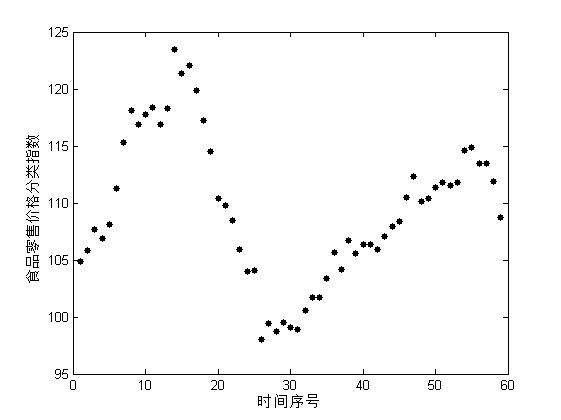
散点图表明x和y的非线性趋势比较明显,可以用多项式曲线进行拟合。
(2)四次多项式拟合
假设y关于x的理论回归方程为:
y=p1*x^4+p2*x^3+p3*x^2+p4*x+p5
其中,p1,p2,p3,p4,p5为未知参数,下面调用polyfit函数求解方程中的未知参数,然后调用poly2sym函数显示多项式的符号表达式
[p4,S4] = polyfit(x,y,4)
r = poly2sym(p4);
r = vpa(r,5) %用vpa函数控制r的精度,保留5位有效数字
p4 =
-0.0001 0.0096 -0.3985 5.5635 94.2769
S4 =
R: [5x5 double]
df: 54
normr: 21.0375
r =
- 0.000074268*x^4 + 0.0096077*x^3 - 0.39845*x^2 + 5.5635*x + 94.277 %与p4向量不完全一致是由于舍入误差的原因
(3)更高次多项式拟合
下面调用polyfit函做更高次(>4)多项式拟合,并把多次拟合的残差的模加以对比
[p5,S5] = polyfit(x,y,5);
S5_normr=S5.normr
[p6,S6] = polyfit(x,y,6);
S6_normr=S6.normr
[p7,S7] = polyfit(x,y,7);
S7_normr=S7.normr
[p8,S8] = polyfit(x,y,8);
S8_normr=S8.normr
[p9,S9] = polyfit(x,y,9);
S9_normr=S9.normr
S5_normr =
21.0359
S6_normr =
16.7662
S7_normr =
12.3067
S8_normr =
11.1946
S9_normr =
10.4050
结果表明,随着多项式次数的提高,残差的模呈下降趋势,单纯从拟合的角度来看,拟合精度会随着多项式次数的提高而提高。
(4)拟合效果图
调用polyval函数计算给定自变量x处的因变量y的预测值,来绘制拟合效果图,从效果图上直观的观察出拟合的准确性
figure;
plot(x,y,'k.','Markersize',15); %x和y的散点图
xlabel('时间序号');
ylabel('食品零售价格分类指数');
hold on;
yd4 = polyval(p4,x);%计算4次多项式拟合的预测值
yd6 = polyval(p6,x);%计算6次多项式
yd8 = polyval(p8,x);% 8次多项式
yd9 = polyval(p9,x);% 9次多项式
plot(x,yd4,'r:+'); %绘制4次多项式拟合曲线
plot(x,yd6,'b--s'); % 6
plot(x,yd8,'g-.d'); % 8
plot(x,yd9,'k-p'); % 9
legend('原始散点','4次多项式拟合','6次多项式拟合','8次多项式拟合','9次多项式拟合')
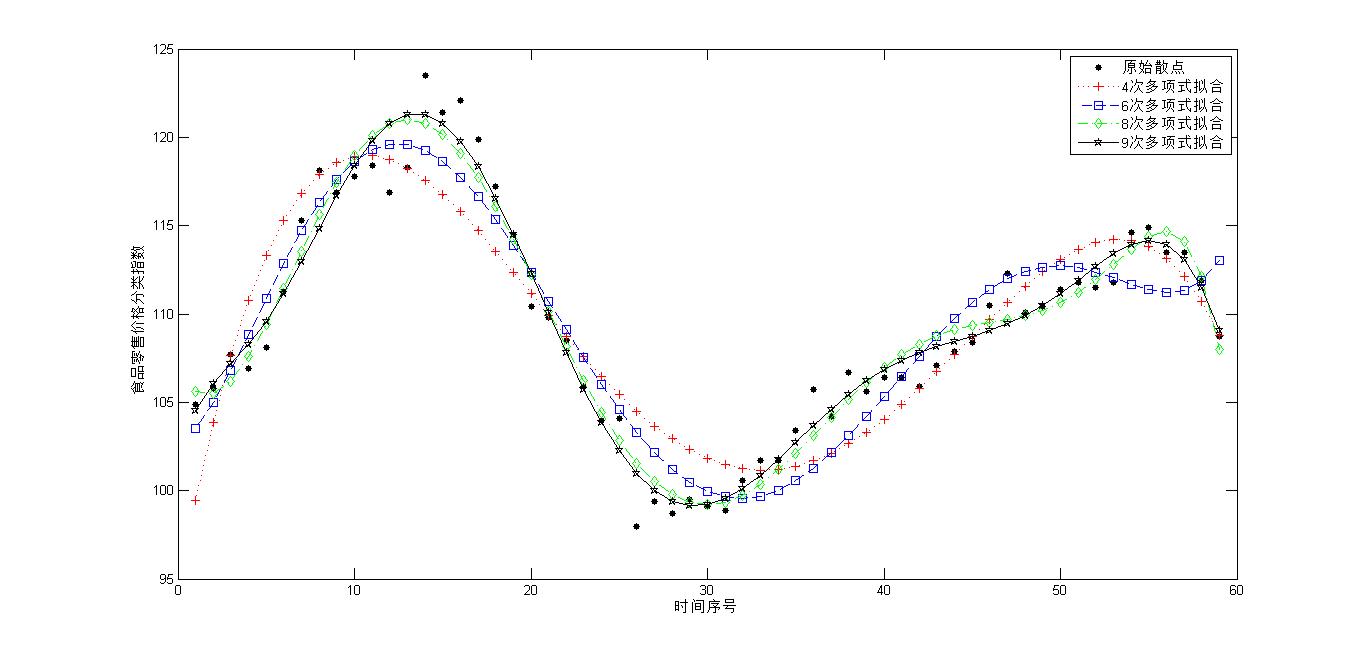
由图中可以看出,高阶多项式的拟合效果比低阶的效果好。
更多MATLAB数据分析视频请点击,或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016
最后
以上就是欣慰手链最近收集整理的关于11.回归分析的全部内容,更多相关11内容请搜索靠谱客的其他文章。








发表评论 取消回复