1. 线性回归思想

1.1 线性回归算法思路

• 线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为，为误差服从均值为0的正态分布。
• 回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
• 简单的说：线性回归对于输入x与输出y有一个映射f，,而f的形式为。其中a和b是两个可调的参数，我们训练的时候就是训练a，b这两个参数。
• 多元线性回归用一个线性方程来适配观察数据，这个线性方程有两个及以上的特征和响应之间构建一个关系。可以用来找出预测结果上哪个因素影响力最大，以及不同变量之间如何相互关联的。

例如：对房价的预测。但是有人可能会问，为什么对于房价的预测就应该用线性回归，而不是其它算法呢？原因在于：常识告诉我们房价都是随着面积的增长而增长的，且总体上呈线性增长的趋势。基本不存在那种当面积大到一定程度后价格反而降低了。

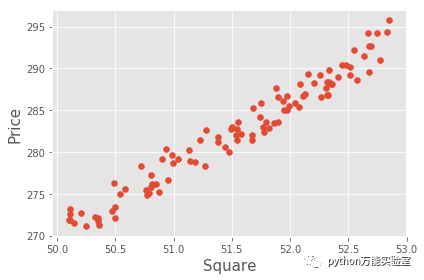如图所示为某房价的一个走势图，其中横坐标为面积，纵坐标为价格，且房价整体上呈线性增长的趋势。那假如随意告诉你一个房屋的面积，怎么才能预测出其对应的价格呢？

1.2 线性回归算法前提

• 线性：自变量和因变量的关系应该是线性的(即特征值和预测值是线性相关)；
• 保持误差项的方差(分散)等同；
• 多元正态分布：多元回归假定残差符合正态分布。

k-means算法中文名叫做k均值。它是一种非监督聚类算法，如有一堆数据，但是知道这些数据有k个类，具体每一个数据点所属分类不知道。此时就需要用k-means聚类算法，它可以把原先的数据分成k个部分，相似的数据就聚在一起。

2. 线性回归模型

2.1 如何建立模型

机器学习中所谓的模型，简单理解就是一个(复合)函数。当我们拿到一个实际问题时首先会根据问题的背景结合常识选择一个合适的模型。同时，现在常识告诉我们房价的增长更优先符合线性回归这类模型，因此可以考虑建立一个如下的线性回归模型：其中叫权重参数(weight)，叫偏置(bias)或者截距(intercept)。当求解得到未知参数之后也就意味着我们得到了预测模型，即给定一个房屋面积，就能够预测出其对应的房价。

2.2 如何求解模型

当我们建立好一个模型后，如何通过给定的数据，也叫训练集(traing data)来对模型进行求解呢？当满足一个什么样的条件时，它才能称得上是一个好的模型? 就是希望输入面积x后能够输出"准确"的房价 h(x)。既然直接求解不好入手，那么我们就从“准确”来入手。

那又怎么来定义准确呢？在这里我们可以通过计算每个样本的真实房价与预测房价之间的均方误差来进行刻画,均方误差来，均方误差越小，说明准确度越高：

其中，表示总的样本数，表示第个样本的，也就是第个房屋的面积，表示第个房屋的真实价格，表示第个房屋的预测价格.

当函数取最小值时的参数，就是我们要求的目标参数。为什么？因为当取最小值就意味着此时所有样本的预测值与真实值之间的误差(error)是最小的。如果极端一点，那就是所有预测值都等同于真实值，此时的就是0了。因此，对于如何求解模型的问题就转换为如何最小化函数的问题了。其实有一个专门的术语叫目标函数(objective function)或者是代价函数(cost function)亦或是损失函数。

3 利用Scikit-learn进行线性回归建模

3.1 制作样本(数据集)

import numpy as npfrom sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as pltdef make_data():    np.random.seed(20)    x = np.random.rand(100) * 30 + 50  # square    noise = np.random.rand(100) * 50    y = x * 8 - 127  # price    y = y - noise    return x, y

3.2 定义模型并求解

def main(x, y):    model = LinearRegression()# 定义模型    x = np.reshape(x, (-1, 1))    model.fit(np.reshape(x, (-1, 1)), y)# 求解模型    y_pre = model.predict(x)# 预测    plt.scatter(x, y)    print("参数w={},b={}".format(model.coef_,model.intercept_))    print("面积50的房价为：",model.predict([[50]]))    plt.plot(x, y_pre, c='r')    plt.xlabel('Square', fontsize=15)    plt.ylabel('Price', fontsize=15)    plt.tight_layout()  # 调整子图间距    plt.show()

其中np.reshape(x,(-1,1))表示把x变成[n,1]的形状，至于n到底应该是多少，将通过np.reshape函数自己推导得出。距离：x的shape为[4,5]，如果我想把a改成[2,10]形状则可以这样：a.reshape([2,10])，或者a.reshape([2,-1])

3.3 运行及结果

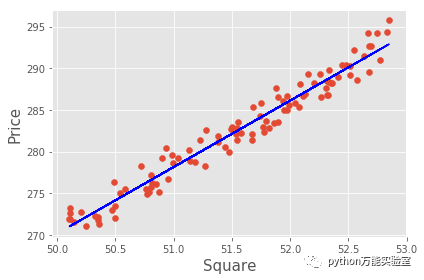
if __name__ == '__main__':    x, y = make_data()    main(x, y)# 输出结果：#参数w=[7.97699647],b=-154.31885006061555#面积50的房价为：[244.53097351]

其中参数 也就是:，之后便可以通过来对新的输入做预测。同时我们还能画出模型拟合出的直线:

4 小结

今天总结了机器学习的线性回归算法的思想原理和模型:

• 线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法；
• 将线性回归模型的求解问题，转化为目标函数的最小化过程。