文章目录
- 循环神经网络 Recurrent Neural Networks
- 前向传播
- 代价函数
- 反向传播
- 语言模型
- 门控循环单元 GRU (gated recurrent units)
- 长短时记忆单元 LSTM (long short time memory)
- 双向RNN (bidirectional RNN)
- 深层RNN
循环神经网络 Recurrent Neural Networks
前向传播
many-to-many 结构
y
^
<
1
>
y
^
<
2
>
y
^
<
3
>
y
^
<
T
>
↑
↑
↑
↑
a
<
0
>
→
◯
◯
◯
◯
→
a
<
1
>
◯
◯
◯
◯
→
a
<
2
>
◯
◯
◯
◯
→
⋯
→
◯
◯
◯
◯
↑
↑
↑
↑
x
<
1
>
x
<
2
>
x
<
3
>
x
<
T
>
begin{array}{ccccccccc} & hat{y}^{<1>} && hat{y}^{<2>} && hat{y}^{<3>} & & hat{y}^{<T>} \ & uparrow && uparrow && uparrow && uparrow\ a^{<0>} rightarrow & boxed{begin{matrix} bigcirc \ bigcirc \ bigcirc \ bigcirc end{matrix}} & xrightarrow{a^{<1>}} & boxed{begin{matrix} bigcirc \ bigcirc \ bigcirc \ bigcirc end{matrix}} & xrightarrow{a^{<2>}} & boxed{begin{matrix} bigcirc \ bigcirc \ bigcirc \ bigcirc end{matrix}} & rightarrow cdots rightarrow & boxed{begin{matrix} bigcirc \ bigcirc \ bigcirc \ bigcirc end{matrix}} \ & uparrow && uparrow && uparrow && uparrow\ & x^{<1>} && x^{<2>} && x^{<3>} & & x^{<T>} \ end{array}
a<0>→y^<1>↑◯◯◯◯↑x<1>a<1>y^<2>↑◯◯◯◯↑x<2>a<2>y^<3>↑◯◯◯◯↑x<3>→⋯→y^<T>↑◯◯◯◯↑x<T>
或者表示成:
y ^ < 1 > y ^ < 2 > y ^ < T > ↑ ↑ ↑ a < 0 > → a < 1 > → a < 2 > → ⋯ → a < T > ↑ ↑ ↑ x < 1 > x < 2 > x < T > begin{array}{ccccccccc} & hat{y}^{<1>} && hat{y}^{<2>} & & hat{y}^{<T>} \ & uparrow && uparrow & & uparrow\ a^{<0>} rightarrow & boxed{a^{<1>}} & rightarrow & boxed{a^{<2>}} & rightarrow cdots rightarrow & boxed{a^{<T>}} \ & uparrow && uparrow && uparrow \ & x^{<1>} && x^{<2>} & & x^{<T>} \ end{array} a<0>→y^<1>↑a<1>↑x<1>→y^<2>↑a<2>↑x<2>→⋯→y^<T>↑a<T>↑x<T>
数学表达式:
a
<
0
>
=
0
⃗
a
<
1
>
=
g
1
(
W
a
a
a
<
0
>
+
W
a
x
x
<
1
>
+
b
a
)
=
g
1
(
W
a
[
a
<
0
>
,
x
<
1
>
]
+
b
a
)
y
<
1
>
=
g
2
(
W
y
a
<
1
>
+
b
y
)
⋮
a
<
T
>
=
g
1
(
W
a
a
a
<
T
−
1
>
+
W
a
x
x
<
T
−
1
>
+
b
a
)
=
g
1
(
W
a
[
a
<
T
−
1
>
,
x
<
t
>
]
+
b
a
)
y
<
T
>
=
g
2
(
W
y
a
<
T
>
+
b
y
)
begin{aligned} a^{<0>} &= vec{0} \ a^{<1>} &= g_{1}(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_{a}) = g_{1}(W_{a}[a^{<0>},x^{<1>}] + b_{a})\ y^{<1>} &= g_{2}(W_{y}a^{<1>} + b_{y}) \ vdots \ a^{<T>} &= g_{1}(W_{aa}a^{<T-1>} + W_{ax}x^{<T-1>} + b_{a}) = g_{1}(W_{a}[a^{<T-1>},x^{<t>}] + b_{a})\ y^{<T>} &= g_{2}(W_{y}a^{<T>} + b_{y}) \ end{aligned}
a<0>a<1>y<1>⋮a<T>y<T>=0=g1(Waaa<0>+Waxx<1>+ba)=g1(Wa[a<0>,x<1>]+ba)=g2(Wya<1>+by)=g1(Waaa<T−1>+Waxx<T−1>+ba)=g1(Wa[a<T−1>,x<t>]+ba)=g2(Wya<T>+by) 其中,激活函数
g
1
g_{1}
g1 通常取 tanh 或 relu,
g
2
g_{2}
g2 取 sigmoid.
many-to-one 结构
例:输入一部影片,进行用户情感分析(喜欢/不喜欢)
y
^
<
T
>
↑
a
<
0
>
→
a
<
1
>
→
a
<
2
>
→
⋯
→
a
<
T
>
↑
↑
↑
x
<
1
>
x
<
2
>
x
<
T
>
begin{array}{ccccccccc} &&&& & hat{y}^{<T>} \ &&&& & uparrow\ a^{<0>} rightarrow & boxed{a^{<1>}} & rightarrow & boxed{a^{<2>}} & rightarrow cdots rightarrow & boxed{a^{<T>}} \ & uparrow && uparrow && uparrow \ & x^{<1>} && x^{<2>} & & x^{<T>} \ end{array}
a<0>→a<1>↑x<1>→a<2>↑x<2>→⋯→y^<T>↑a<T>↑x<T>
one-to-one 结构
y
^
↑
a
<
0
>
→
a
<
1
>
↑
x
begin{array}{ccc} & hat{y} \ & uparrow\ a^{<0>} rightarrow & boxed{a^{<1>}} \ & uparrow \ & x \ end{array}
a<0>→y^↑a<1>↑x
one-to-many 结构:如音乐生成器
y
^
<
1
>
y
^
<
2
>
y
^
<
T
>
↑
↑
↑
a
<
0
>
→
a
<
1
>
→
a
<
2
>
→
⋯
→
a
<
T
>
↑
x
或
ϕ
begin{array}{cccccc} & hat{y}^{<1>} && hat{y}^{<2>} & & hat{y}^{<T>} \ & uparrow && uparrow & & uparrow\ a^{<0>} rightarrow & boxed{a^{<1>}} & rightarrow & boxed{a^{<2>}} & rightarrow cdots rightarrow & boxed{a^{<T>}} \ & uparrow\ & x或phi \ end{array}
a<0>→y^<1>↑a<1>↑x或ϕ→y^<2>↑a<2>→⋯→y^<T>↑a<T>
其他many-to-many结构:
y
^
<
1
>
y
^
<
T
y
>
↑
↑
a
<
0
>
→
a
<
1
>
→
⋯
→
a
<
T
x
>
→
a
<
T
x
+
1
>
→
⋯
→
a
<
T
x
+
T
y
>
↑
↑
x
<
1
>
x
<
T
x
>
begin{array}{ccccccccc} &&&&& hat{y}^{<1>} && hat{y}^{<T_{y}>} \ &&&&& uparrow && uparrow\ a^{<0>} rightarrow & boxed{a^{<1>}} & rightarrow cdots rightarrow & boxed{a^{<T_{x}>}} & rightarrow & boxed{a^{<T_{x}+1>}} & rightarrow cdots rightarrow & boxed{a^{<T_{x}+T_{y}>}} \ & uparrow && uparrow\ & x^{<1>} && x^{<T_{x}>} \ end{array}
a<0>→a<1>↑x<1>→⋯→a<Tx>↑x<Tx>→y^<1>↑a<Tx+1>→⋯→y^<Ty>↑a<Tx+Ty>
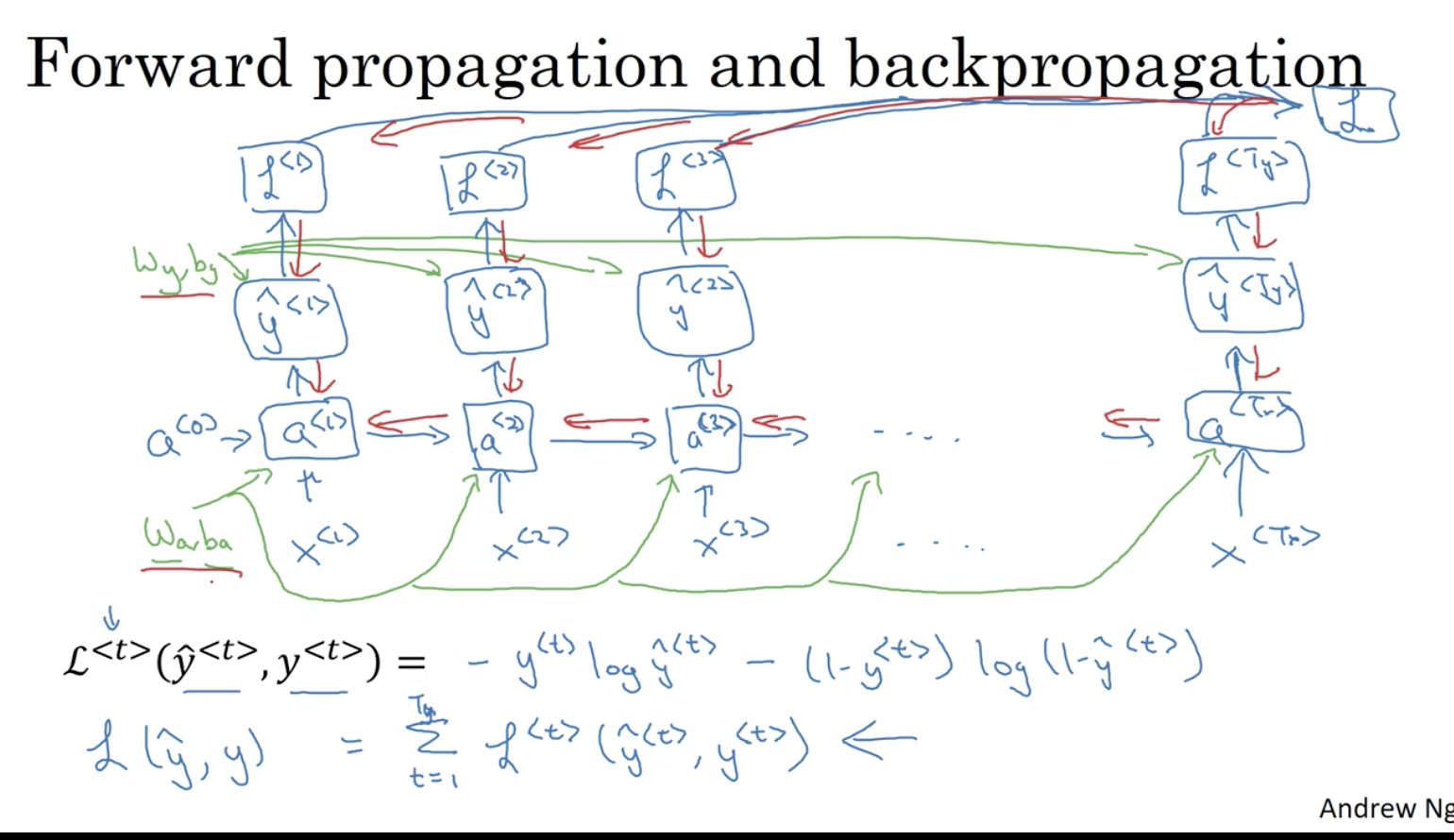
代价函数
L ( y ^ , y ) = ∑ t = 1 T L < t > ( y ^ < t > , y < t > ) L(hat{y}, y) = sum_{t=1}^{T} L^{<t>}(hat{y}^{<t>}, y^{<t>}) L(y^,y)=t=1∑TL<t>(y^<t>,y<t>) 其中, L < t > ( y ^ < t > , y < t > ) = − y < t > log y ^ < t > − ( 1 − y < t > ) log ( 1 − y ^ < t > ) L^{<t>}(hat{y}^{<t>}, y^{<t>}) = -y^{<t>}loghat{y}^{<t>} - (1-y^{<t>})log(1-hat{y}^{<t>}) L<t>(y^<t>,y<t>)=−y<t>logy^<t>−(1−y<t>)log(1−y^<t>)
反向传播
仅以 many-to-many 为例:
语言模型
RNN模型
对一个语言序列
(
y
<
1
>
,
y
<
2
>
,
⋯
,
y
<
T
>
)
(y^{<1>}, y^{<2>}, cdots, y^{<T>})
(y<1>,y<2>,⋯,y<T>),建立以下模型计算该序列的概率:
y
^
<
1
>
∥
P
(
y
<
1
>
)
y
^
<
2
>
∥
P
(
y
<
2
>
∣
y
<
1
>
)
y
^
<
T
>
∥
P
(
y
<
T
>
∣
y
<
1
>
,
⋯
,
y
<
T
−
1
>
)
↑
↑
↑
a
<
0
>
=
0
⃗
→
a
<
1
>
→
a
<
2
>
→
⋯
→
a
<
T
>
↑
↑
↑
x
<
1
>
=
0
⃗
y
<
1
>
y
<
T
−
1
>
begin{array}{ccccccccc} &&begin{matrix}hat{y}^{<1>} \ shortparallel\ P(y^{<1>}) end{matrix} && begin{matrix}hat{y}^{<2>} \ shortparallel\ P(y^{<2>}|y^{<1>}) end{matrix} & & begin{matrix} hat{y}^{<T>} \ shortparallel \ P(y^{<T>}|y^{<1>},cdots,y^{<T-1>}) end{matrix}\ && uparrow && uparrow & & uparrow\ a^{<0>}=vec{0} &rightarrow & boxed{a^{<1>}} & rightarrow & boxed{a^{<2>}} & rightarrow cdots rightarrow & boxed{a^{<T>}} \ && uparrow && uparrow && uparrow \ && x^{<1>}=vec{0} && y^{<1>}& & y^{<T-1>} \ end{array}
a<0>=0→y^<1>∥P(y<1>)↑a<1>↑x<1>=0→y^<2>∥P(y<2>∣y<1>)↑a<2>↑y<1>→⋯→y^<T>∥P(y<T>∣y<1>,⋯,y<T−1>)↑a<T>↑y<T−1>
则
P
(
y
<
1
>
,
y
<
2
>
,
⋯
,
y
<
T
>
)
=
P
(
y
<
1
>
)
P
(
y
<
2
>
∣
y
<
1
>
)
⋯
P
(
y
<
T
>
∣
y
<
1
>
,
⋯
,
y
<
T
−
1
>
)
P(y^{<1>}, y^{<2>}, cdots, y^{<T>}) = P(y^{<1>})P(y^{<2>}|y^{<1>})cdots P(y^{<T>}|y^{<1>},cdots,y^{<T-1>})
P(y<1>,y<2>,⋯,y<T>)=P(y<1>)P(y<2>∣y<1>)⋯P(y<T>∣y<1>,⋯,y<T−1>)
损失函数
L
(
y
^
,
y
)
=
−
∑
t
L
(
y
^
<
t
>
,
y
<
t
>
)
L(hat{y},y) = -sum_{t}L(hat{y}^{<t>},{y}^{<t>})
L(y^,y)=−t∑L(y^<t>,y<t>) 其中,
L
(
y
^
<
t
>
,
y
<
t
>
)
=
−
∑
i
y
i
<
t
>
log
y
^
<
t
>
L(hat{y}^{<t>},{y}^{<t>}) = -sum_{i}y_{i}^{<t>}loghat{y}^{<t>}
L(y^<t>,y<t>)=−i∑yi<t>logy^<t>
训练好模型后如何采样?
y
^
<
1
>
∥
arg
max
P
(
y
<
1
>
)
y
^
<
2
>
∥
arg
max
P
(
y
<
2
>
∣
y
^
<
1
>
)
y
^
<
T
>
∥
arg
max
P
(
y
<
T
>
∣
y
^
<
1
>
,
⋯
,
y
^
<
T
−
1
>
)
↑
↑
↑
a
<
0
>
=
0
⃗
→
a
<
1
>
→
a
<
2
>
→
⋯
→
a
<
T
>
↑
↑
↑
x
<
1
>
=
0
⃗
y
^
<
1
>
y
^
<
T
−
1
>
begin{array}{ccccccccc} &&begin{matrix}hat{y}^{<1>} \ shortparallel\ {argmax}{P(y^{<1>})} end{matrix} & & begin{matrix}hat{y}^{<2>} \ shortparallel\ {argmax}P(y^{<2>}|hat{y}^{<1>}) end{matrix} & & begin{matrix} hat{y}^{<T>} \ shortparallel \ {argmax}P(y^{<T>}|hat{y}^{<1>},cdots,hat{y}^{<T-1>}) end{matrix}\ && uparrow && uparrow & & uparrow\ a^{<0>}=vec{0} &rightarrow & boxed{a^{<1>}} & rightarrow & boxed{a^{<2>}} & rightarrow cdots rightarrow & boxed{a^{<T>}} \ && uparrow && uparrow && uparrow \ && x^{<1>}=vec{0} && hat{y}^{<1>}& & hat{y}^{<T-1>} \ end{array}
a<0>=0→y^<1>∥argmaxP(y<1>)↑a<1>↑x<1>=0→y^<2>∥argmaxP(y<2>∣y^<1>)↑a<2>↑y^<1>→⋯→y^<T>∥argmaxP(y<T>∣y^<1>,⋯,y^<T−1>)↑a<T>↑y^<T−1>
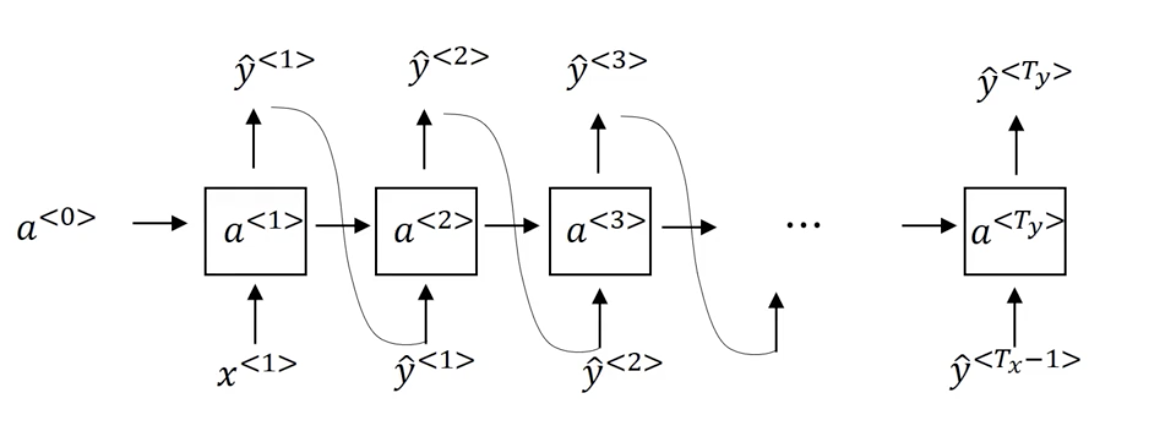
可以以<EOS>为结束标志。
门控循环单元 GRU (gated recurrent units)
解决梯度消失问题
c:memory cell
c
~
<
t
>
=
tanh
(
W
c
[
Γ
r
×
c
<
t
−
1
>
,
x
<
t
>
]
+
b
c
)
相
关
门
:
Γ
r
=
σ
(
W
r
[
c
<
t
−
1
>
,
x
<
t
>
]
+
b
r
)
更
新
门
:
Γ
u
=
σ
(
W
u
[
c
<
t
−
1
>
,
x
<
t
>
]
+
b
u
)
c
<
t
>
=
Γ
u
×
c
~
<
t
>
+
(
1
−
Γ
u
)
×
c
<
t
−
1
>
a
<
t
>
=
c
<
t
>
begin{aligned} tilde c^{<t>} &= tanh(W_{c}[Gamma_{r} times c^{<t-1>},x^{<t>}] + b_{c}) \ 相关门:Gamma_{r} &= sigma(W_{r}[c^{<t-1>},x^{<t>}] + b_{r}) \ 更新门:Gamma_{u} &= sigma(W_{u}[c^{<t-1>},x^{<t>}] + b_{u}) \ c^{<t>} &= Gamma_{u}times tilde c^{<t>} + (1-Gamma_{u}) times c^{<t-1>} \ a^{<t>} &= c^{<t>}\ end{aligned}
c~<t>相关门:Γr更新门:Γuc<t>a<t>=tanh(Wc[Γr×c<t−1>,x<t>]+bc)=σ(Wr[c<t−1>,x<t>]+br)=σ(Wu[c<t−1>,x<t>]+bu)=Γu×c~<t>+(1−Γu)×c<t−1>=c<t> 当
Γ
u
≈
1
Gamma_{u} approx 1
Γu≈1 时,
c
<
t
>
≈
c
<
t
−
1
>
c^{<t>} approx c^{<t-1>}
c<t>≈c<t−1>.
长短时记忆单元 LSTM (long short time memory)
c
~
<
t
>
=
tanh
(
W
c
[
a
<
t
−
1
>
,
x
<
t
>
]
+
b
c
)
更
新
门
:
Γ
u
=
σ
(
W
u
[
a
<
t
−
1
>
,
x
<
t
>
]
+
b
u
)
遗
忘
门
:
Γ
f
=
σ
(
W
f
[
a
<
t
−
1
>
,
x
<
t
>
]
+
b
f
)
输
出
门
:
Γ
o
=
σ
(
W
o
[
a
<
t
−
1
>
,
x
<
t
>
]
+
b
o
)
c
<
t
>
=
Γ
u
×
c
~
<
t
>
+
Γ
f
×
c
<
t
−
1
>
a
<
t
>
=
Γ
o
×
c
<
t
>
begin{aligned} tilde c^{<t>} &= tanh(W_{c}[a^{<t-1>},x^{<t>}] + b_{c}) \ 更新门:Gamma_{u} &= sigma(W_{u}[a^{<t-1>},x^{<t>}] + b_{u}) \ 遗忘门:Gamma_{f} &= sigma(W_{f}[a^{<t-1>},x^{<t>}] + b_{f}) \ 输出门:Gamma_{o} &= sigma(W_{o}[a^{<t-1>},x^{<t>}] + b_{o}) \ c^{<t>} &= Gamma_{u}times tilde c^{<t>} + Gamma_{f} times c^{<t-1>} \ a^{<t>} &= Gamma_{o} times c^{<t>} end{aligned}
c~<t>更新门:Γu遗忘门:Γf输出门:Γoc<t>a<t>=tanh(Wc[a<t−1>,x<t>]+bc)=σ(Wu[a<t−1>,x<t>]+bu)=σ(Wf[a<t−1>,x<t>]+bf)=σ(Wo[a<t−1>,x<t>]+bo)=Γu×c~<t>+Γf×c<t−1>=Γo×c<t>
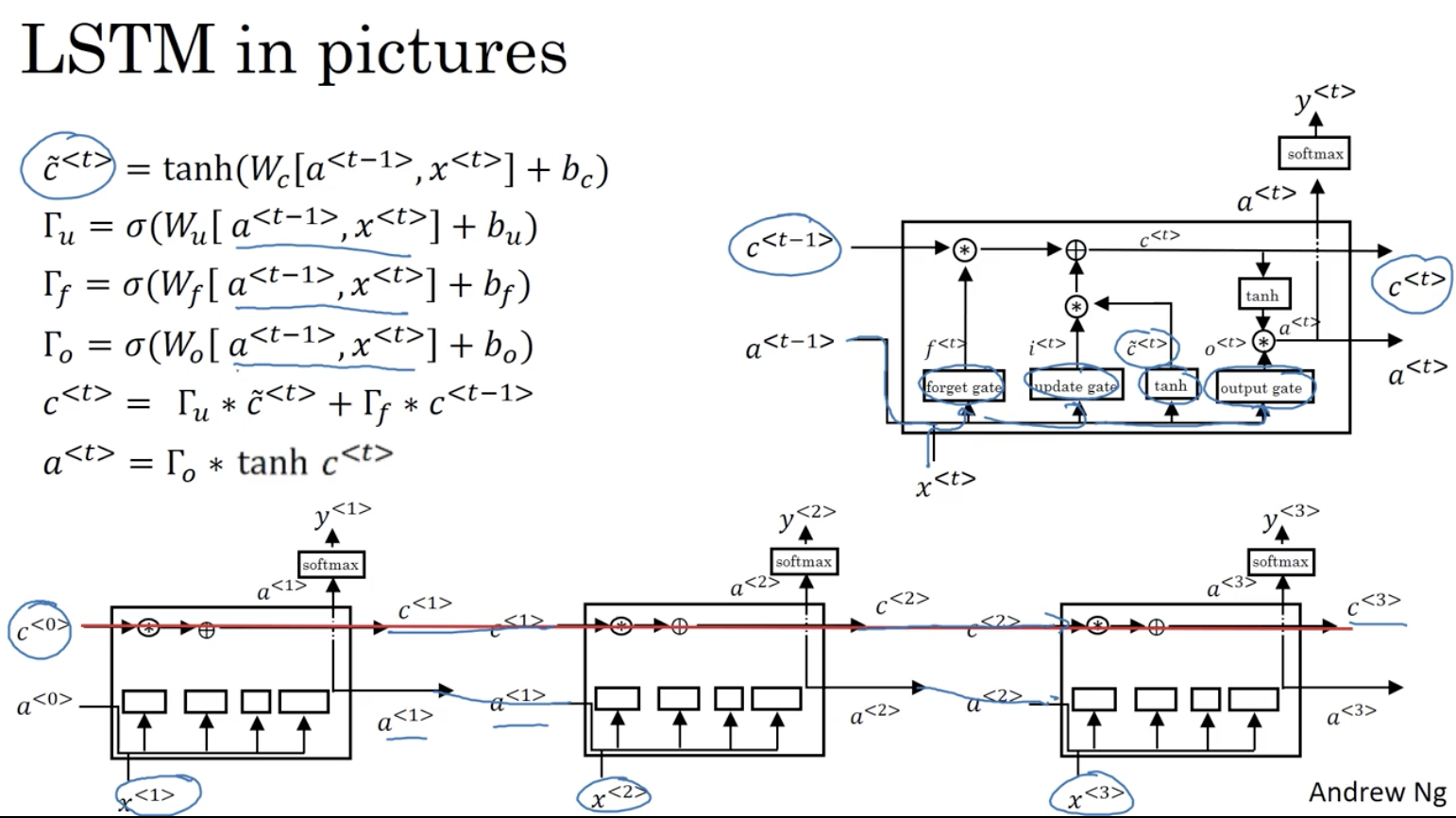
GRU or LSTM ?
GRU 只有两个门控,更简单,可以看成是LSTM的简化;
LSTM 有三个门控,更强大和灵活。
双向RNN (bidirectional RNN)
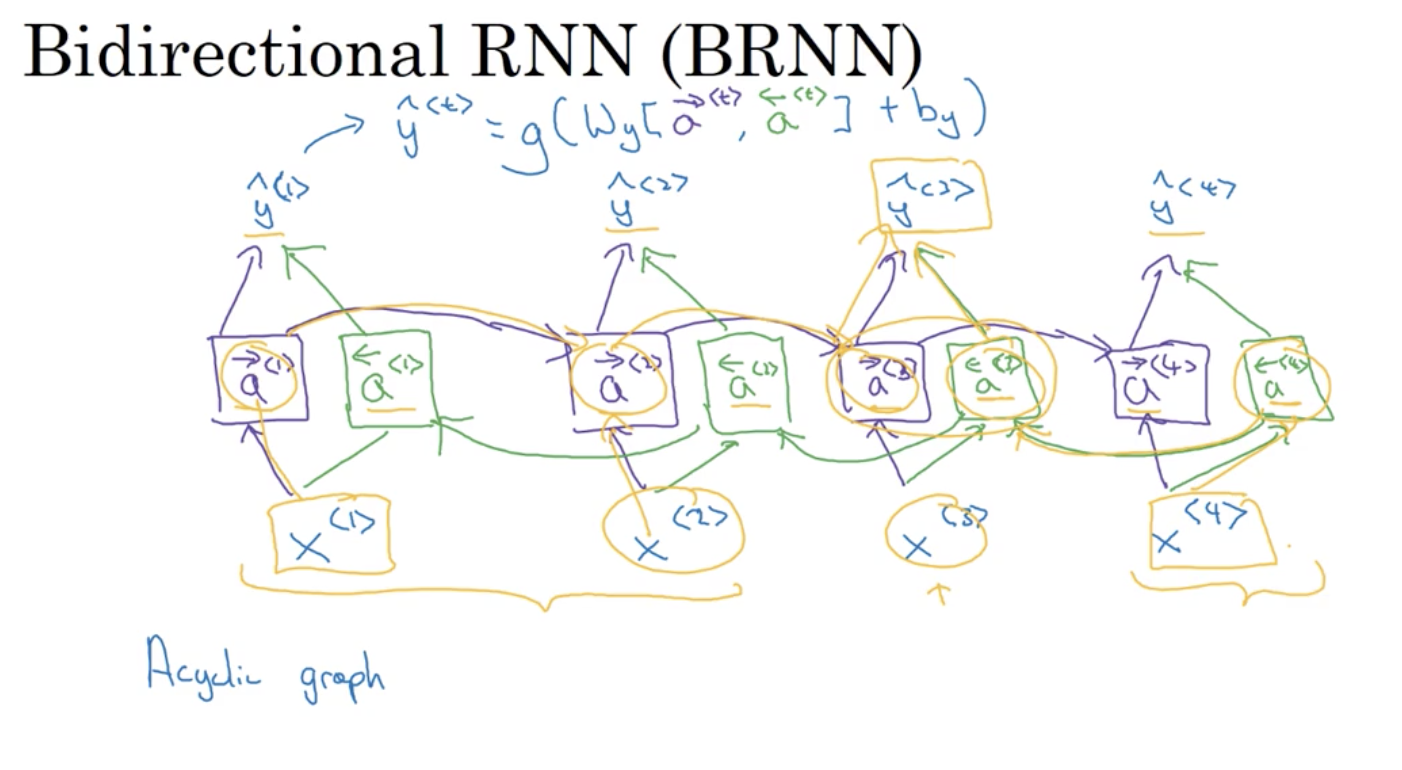
如对于输出
y
^
<
3
>
hat{y}^{<3>}
y^<3>,即收到了来自过去
x
<
1
>
,
x
<
2
>
x^{<1>}, x^{<2>}
x<1>,x<2> 的信息,又收到了来自现在
x
<
3
>
x^{<3>}
x<3>,也收到了来自未来
x
<
4
>
x^{<4>}
x<4> 的信息。
在处理NLP问题中,带有LSTM的双向RNN是非常常用的。
深层RNN
y ^ < 1 > y ^ < 2 > y ^ < T > ↑ ↑ ↑ a [ 3 ] < 0 > → a [ 3 ] < 1 > → a [ 3 ] < 2 > → ⋯ → a [ 3 ] < T > ↑ ↑ ↑ a [ 2 ] < 0 > → a [ 2 ] < 1 > → a [ 2 ] < 2 > → ⋯ → a [ 2 ] < T > ↑ ↑ ↑ a [ 1 ] < 0 > → a [ 1 ] < 1 > → a [ 1 ] < 2 > → ⋯ → a [ 1 ] < T > ↑ ↑ ↑ x < 1 > x < 2 > x < T > begin{array}{ccccccccc} & hat{y}^{<1>} && hat{y}^{<2>} & & hat{y}^{<T>} \ & uparrow && uparrow & & uparrow\ a^{[3]<0>} rightarrow & boxed{a^{[3]<1>}} & rightarrow & boxed{a^{[3]<2>}} & rightarrow cdots rightarrow & boxed{a^{[3]<T>}} \ & uparrow && uparrow & & uparrow\ a^{[2]<0>} rightarrow & boxed{a^{[2]<1>}} & rightarrow & boxed{a^{[2]<2>}} & rightarrow cdots rightarrow & boxed{a^{[2]<T>}} \ & uparrow && uparrow & & uparrow\ a^{[1]<0>} rightarrow & boxed{a^{[1]<1>}} & rightarrow & boxed{a^{[1]<2>}} & rightarrow cdots rightarrow & boxed{a^{[1]<T>}} \ & uparrow && uparrow && uparrow \ & x^{<1>} && x^{<2>} & & x^{<T>} \ end{array} a[3]<0>→a[2]<0>→a[1]<0>→y^<1>↑a[3]<1>↑a[2]<1>↑a[1]<1>↑x<1>→→→y^<2>↑a[3]<2>↑a[2]<2>↑a[1]<2>↑x<2>→⋯→→⋯→→⋯→y^<T>↑a[3]<T>↑a[2]<T>↑a[1]<T>↑x<T>
如:其中
a
[
2
]
<
2
>
=
g
(
W
a
[
2
]
[
a
[
2
]
<
1
>
]
,
a
[
1
]
<
2
>
]
+
b
[
2
]
)
a^{[2]<2>} = g(W_{a}^{[2]}[a^{[2]<1>]}, a^{[1]<2>}]+b^{[2]})
a[2]<2>=g(Wa[2][a[2]<1>],a[1]<2>]+b[2])
当然,也可以把其中某些箭头去掉;每一个块不一定是标准的RNN,可以是LSTM或GRU;可以建立双向RNN.
最后
以上就是高兴哈密瓜最近收集整理的关于循环神经网络——序列模型的全部内容,更多相关循环神经网络——序列模型内容请搜索靠谱客的其他文章。








发表评论 取消回复