RNN+LSTM笔记

Naive RNN

概述

循环神经网络（Recurrent Neural Network，RNN）是一种用于处理序列数据的神经网络。相比一般的神经网络来说，他能够处理序列变化的数据。比如某个单词的意思会因为上文提到的内容不同而有不同的含义，RNN就能够很好地解决这类问题，因此在机器翻译、问答系统等NLP领域有很重要的应用。

结构

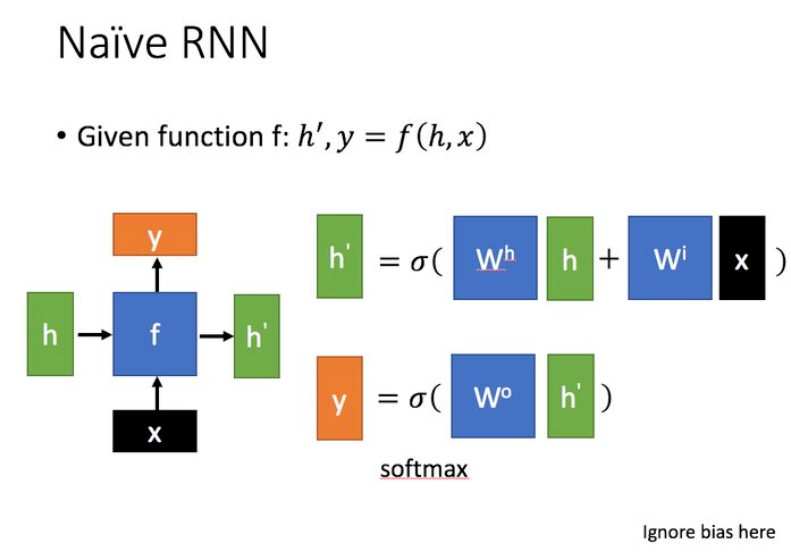
其中，x表示当前状态下数据的输入，h表示接收到的上一个节点的输入，y表示当前状态下的输出，h’表示传递到下一个节点的输出。图中的公式表明了h‘是历史状态（长期记忆）h和当前状态的输入x的线性组合，而y则是对h’进行线性操作。

假设输入为一个序列，则RNN则可以展开成这样的结构：

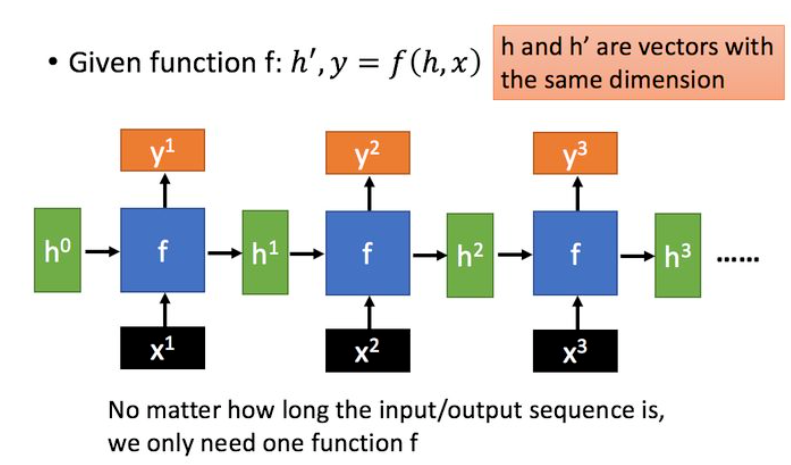
问题

但是实际使用中，RNN具有很严重的梯度消失和梯度爆炸的问题，这是个实践问题，而不是一个理论问题，因为合适的参数一定存在，但是RNN的这组合适的参数不容易找到，这对于RNN来说犹如外卖软件不能点外卖一样致命。

LSTM

概述

LSTM的全称是Long short-term memory，即长短期记忆网络，它有效缓解了RNN中梯度消失的问题（梯度爆炸的问题可以从其他技术中得到缓解），因此在更长的序列上又更优秀的表现。

补充：更加严谨的叫法其实是 LSTM-RNN，即带有长短期记忆网络单元的RNN网络。

外部结构

从输入输出上，LSTM和传统RNN的对比如下所示

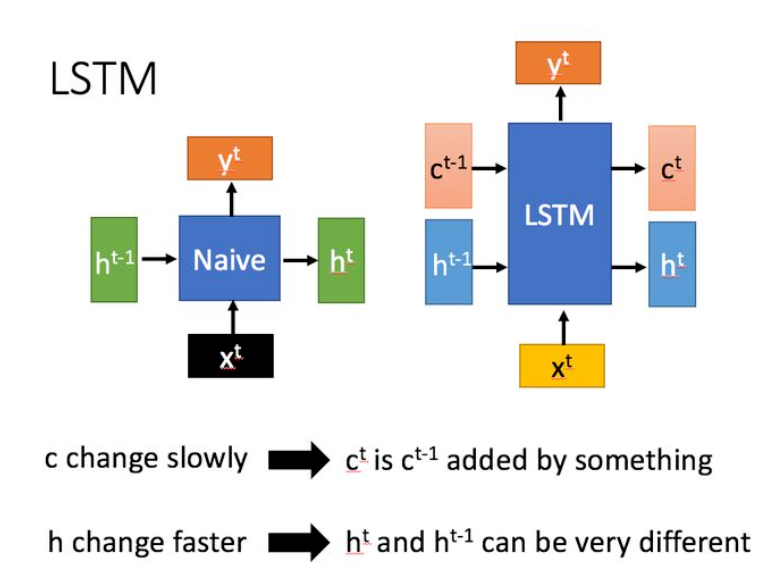
传统RNN只有一个传递状态h，但是LSTM有两个传递状态$c$和$h$，前者代表cell state，是在前一个状态输出的c的基础上调整来的，变化缓慢，所以代表长期记忆（long-term memory）；而后者表示hidden state，因为作为和输入x拼接的变量，因此与相邻LSTM单元的输入值有关，变化较大，所以代表短期记忆（short-term memory）

可见，LSTM中的c反而和naive RNN的h更加相似，代表着long-term memory。

内部结构

首先，第t个LSTM单元的输入为当前输入$x^t$和上一个状态传递下来的short-term memory $h^{t-1}$拼接并训练得到的四个状态：

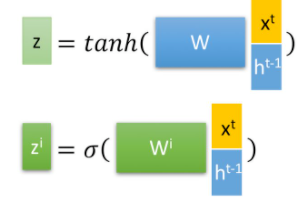
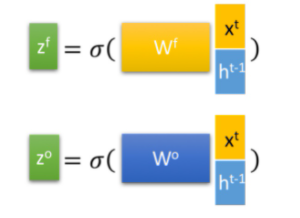
其中，z^f，zⁱ，z^o是由拼接向量乘以权重矩阵之后，再通过一个 sigmoid激活函数转换成0到1之间的数值，来作为一种门控状态，分别表示遗忘门控、输入门控、输出门控。

而 z 则是将结果通过一个tanh激活函数将转换成-1到1之间的值（这里使用 tanh 是因为这里是将其做为输入数据，而不是门控信号，也有人认为，使用tanh也是传递状态c和h不同的本质原因)

下面则是LSTM的内部结构

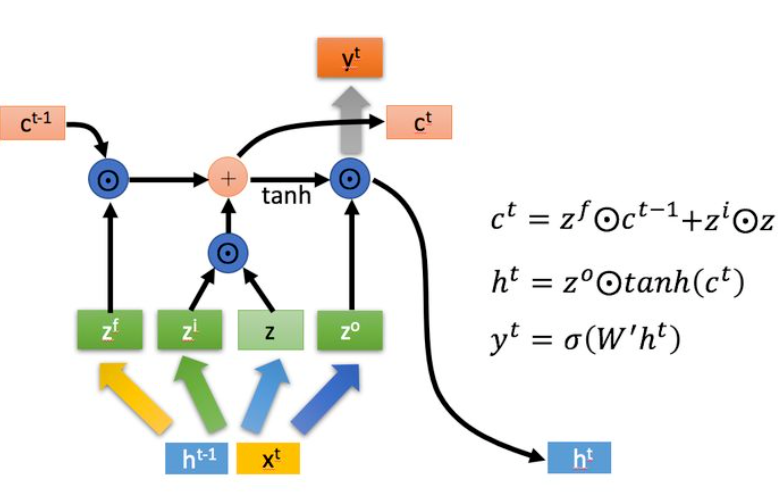
$\odot$代表Hadamard Product，即矩阵对应元素相乘，这要求两个矩阵是同型的，$\oplus$代表矩阵相加。

LSTM主要有三个阶段，分别对应三个门限：

1. 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。具体来讲，就是$z^f$控制$c^{t-1}$的哪些部分需要遗忘。

2. 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入$x^t$进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的$z$表示，而选择的门控信号则是由 $z^i$（有人认为i代表information，也有人认为i代表input）来进行控制。
   将上面两步得到的结果相加，即可得到传输给下一个状态的$c^t$ ，也就是上图中的第一个公式。

3. 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $z^o$来进行控制的，并且还对上一阶段得到的$c^o$进行了放缩（通过一个tanh激活函数进行变化）。

而$y^t$的输出和$h^t$有关，这一点和naive RNN很相似。

为什么LSTM缓解了RNN的梯度消失问题

为什么RNN很容易出现梯度消失

假设使用SGD train RNN模型的参数，则有：
$$w^{i+1}=w^i-r\frac{\partial Loss}{\partial w}{|}_{w:w^i}$$
而naive RNN模型的输出参数的表达式为
$$\begin{gathered} h^{\prime }=\sigma (w^h\cdot h+w^i\cdot x) \\ y=\sigma (w^o\cdot h^{\prime }) \end{gathered}$$
其中，$w^h,w^i,w^o$都是要学习的参数。

接下来我们计算损失函数，这里的损失函数要考虑从0时刻到t时刻的损失函数求和，又称为BPTT(Back Propagation Trough Time)：
$$L=\sum _{t=0}^T{L}_t$$
计算损失函数的梯度：
$$\frac{\partial L}{\partial W}=\sum _{t=0}^T\frac{\partial L_t}{\partial W}$$
分别列出损失函数对三个梯度的求导表达式：
$$\begin{gathered} \frac{\partial L}{\partial W}=\sum _{t=0}^T\frac{\partial L_t}{\partial W}\frac{\partial L_t}{\partial W^o}=\sum _{t=0}^T\frac{\partial L_t}{\partial y_t}\frac{\partial y_t}{\partial W^o} \\ \frac{\partial L_t}{\partial W^i}=\sum _{t=0}^T\sum _{k=0}^t\frac{\partial L_t}{\partial y_t}\frac{\partial y_t}{\partial h_t}\left(\prod _{j=k+1}^t\frac{\partial h_j}{\partial h_{j-1}}\right)\frac{\partial h_k}{\partial W^i} \\ \frac{\partial L_t}{\partial W^h}=\sum _{t=0}^T\sum _{k=0}^t\frac{\partial L_t}{\partial y_t}\frac{\partial y_t}{\partial h_t}\left(\prod _{j=k+1}^t\frac{\partial h_j}{\partial h_{j-1}}\right)\frac{\partial h_k}{\partial W^h} \end{gathered}$$
可见，导致RNN容易梯度消失和爆炸的就是这里的连乘项，其本质是$h_t$对$W^i$求导需要链式求导到最初的$h^k$，为了进一步分析，我们将连乘项中的$h_j$对$h_{j-1}$的导数展开：
$$\frac{\partial h_j}{\partial h_{j-1}}={\sigma }^{\prime }{W}^h=\sigma (1-\sigma )W^h$$
其中，$\sigma (1-\sigma )$的取值范围是(0,0.25)，即如果$W^h$小于4，连乘式的每一项都是小于1的，就很容易发生梯度消失！反之，梯度爆炸则不那么容易发生。

LSTM如何避免了梯度消失

LSTM的BPTT展开式非常复杂，但是核心是将RNN中的连乘式替换为了$c_j$对$c_{j-1}$的求导：
$$\prod _{j=k+1}^t\frac{\partial h_j}{\partial h_{j-1}}\to \prod _{j=k+1}^t\frac{\partial c_j}{\partial c_{j-1}}$$
这也从侧面佐证了我们上面所说的，LSTM中的传递状态c和RNN中的传递状态h都代表着long-term memory。

忽略bias，$c_j$和$c_{j-1}$的关系式为
$$\begin{array}{rl}{c}_j& =\left(z_f\odot c_{j-1}\right)\oplus \left(z_i\odot z\right)\\ & =\left[\sigma \left(W^f{x}_j+b^f\right)\odot c_{j-1}\right]\oplus \left[\sigma \left(W^i{x}_j+b^i\right)\odot \tanh \left(W{x}_j+b\right)\right]\end{array}$$
则$c_j$对$c_{j-1}$的连乘项等于$\sigma (W^f{x}_j+b^f)$，其取值范围是(0,1)，这就不是很容易发生梯度消失了。【注意：此时认为$z^f,z^i,z^o$不是$c_{j-1}$的函数，这其实是很片面的，因为这三者都是$h_{j-1}$的函数，自然也是$c_{j-1}$的函数，下面有完整的梯度分析。】

在LSTM的原始论文中并没有$z_f$这样一个控制遗忘的门控，这会造成cell的状态是不可控的，于是加上遗忘门控，而连乘项的截断梯度的估计正好是$f_t$。

补充：上面的梯度计算并不完整，这篇文章很好的解释了这个问题，Why LSTMs Stop Your Gradients From Vanishing: A View from the Backwards Pass (weberna.github.io)

符号假设为
$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$
完整的梯度是
$$\frac{\partial h_j}{\partial h_{j-1}}={\sigma }^{\prime }{W}^h\frac{\partial C_t}{\partial C_{t-1}}=\frac{\partial C_t}{\partial f_t}\frac{\partial f_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}+\frac{\partial C_t}{\partial i_t}\frac{\partial i_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}+\frac{\partial C_t}{\partial C_{t-1}}\frac{\partial C_{t-1}^{\sim }}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial C_{t-1}}$$
进一步展开
$$\frac{\partial C_t}{\partial C_{t-1}}=C_{t-1}{\sigma }^{\prime }(.)W_f\ast o_{t-1}\tanh \left(C_{t-1}\right)+{\tilde{C}}_t{\sigma }^{\prime }(.)W_i\ast o_{t-1}\tanh \left(C_{t-1}\right)+i_t{\tanh }^{\prime }(.)W_c\ast o_{t-1}\tanh \left(C_{t-1}\right)$$
之前的结果等于$f_t$，一直都是小于1，现在的结果可以大于1也可以小于1，而且$f_t,i_t,o_t,\overline{C_t}$都是网络自己学习的，因此可以很好的避免梯度消失的问题。

参考文献

LSTM介绍

【强烈推荐】 https://zhuanlan.zhihu.com/p/32085405

LSTM为什么能够缓解梯度消失

【截断梯度的分析，有些错误，注意甄别】 https://www.zhihu.com/question/44895610/answer/616818627

【完整的梯度分析】 https://zhuanlan.zhihu.com/p/109519044

最后

以上就是小巧咖啡豆为你收集整理的RNN+LSTM笔记的全部内容，希望文章能够帮你解决RNN+LSTM笔记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。