前言:师兄组会上的一篇文章, 给结构学习提供了新思路, 自己仔细读一读记点笔记.
主要参考文献:
Chen, G., Lu, Y., Su, R., & Kong, Z. (2022). Interpretable Fault Diagnosis of Rolling Element Bearings with Temporal Logic Neural Network. ArXiv. https://doi.org/10.48550/arXiv.2204.07579
文章目录
- 概览
- 流水账笔记
- 1 Introduction
- 2 Preliminaries
- STL
- wSTL
- Weighted robustness degree
- Activation function
- 3 Temporal Logic Neural Network
- Layer 1 (Input layer)
- Layer 2 (Predicate layer)
- Layer 3 (Atomic formula layer)
- Auto-Encoder
- Activation Function
- Layer 4 (Formula reduction layer)
- Layer 5 (Output layer)
- 4 TLNN Learning
- A. Structure learning
- Neuron reduction
- Neuron increase
- B. Parameter Learning
- 5 Case Studies
- 背景介绍
- 结果
- 6 Conclusions
- 心得与记录
概览
本文亮点:
- 用神经网络的反向传播特性来学习公式结构
- 通过结构学习解决的是数据的拟合而非分类问题
- wSTL的引入
流水账笔记
1 Introduction
本文的中心论点其实有点奇怪, 全片放在故障诊断的框架下谈, 但我感觉STL的结构学习算法才是这篇论文的核心.
故障诊断通常是用DL来做的, 但是传统的DL神经网络通常是黑箱一般的存在, 究竟是根据怎样的依据进行分类的不得而知。
因此本文的研究意义是为了给DL提供形式化解释——时序逻辑的可解释性便为DL可解释性的研究提供了一条新思路.
TLNN的主要思想: 用神经网络编码STL的公式结构
2 Preliminaries
STL
之前介绍过很多次了, 这里不再赘述。
wSTL
wSTL的定义是使用神经网络的基础. 这里重点要搞清楚wSTL和STL有什么样的区别. 顾名思义, wSTL多了一个权重的概念, 那么这个权重是加在哪里呢?
φ : = μ ∣ ¬ φ ∣ ∧ i = 1 : N w φ i ∣ ∨ i = 1 : N w φ i ∣ ∇ [ τ 1 , τ 2 ) w φ ∣ □ [ τ 1 , τ 2 ) w φ varphi:=mu|neg varphi| wedge_{i=1: N}^{w} varphi_{i}left|vee_{i=1: N}^{w} varphi_{i}right| nabla_{left[tau_{1}, tau_{2}right)}^{w} varphi mid square_{left[tau_{1}, tau_{2}right)}^{w} varphi φ:=μ∣¬φ∣∧i=1:Nwφi∣∨i=1:Nwφi∣∇[τ1,τ2)wφ∣□[τ1,τ2)wφ
- 对于布尔操作子, 权重加在子公式上
- 对于时序操作子, 权重加在不同的时间点上.
Weighted robustness degree
定义:
ρ w ( x , f ( x ) ≥ c , t ) : = w 2 ( f ( x ( t ) ) − c ) ρ w ( x , f ( x ) < c , t ) : = w 2 ( c − f ( x ( t ) ) ) ρ w ( x , ¬ φ , t ) : = − ρ w ( x , φ , t ) ρ w ( x , ∧ i = 1 : N w φ i , t ) : = g ∧ ( w , [ ρ w ( x , φ i , t ) ] i = 1 : N ) ρ w ( x , ∨ i = 1 : N w φ i , t ) : = g ∨ ( w , [ ρ w ( x , φ i , t ) ] i = 1 : N ) ρ w ( x , □ [ τ 1 , τ 2 ] w φ , t ) : = g □ ( w , [ ρ w ( x , φ , t ) ] t ′ ∈ [ t + τ 1 , t + τ 2 ] ) ρ w ( x , ⋄ [ τ 1 , τ 2 ] φ , t ) : = g ⋄ ( w , [ ρ w ( x , φ , t ) ] t ′ ∈ [ t + τ 1 , t + τ 2 ] ) begin{array}{ll}rho^{w}(x, f(x) geq c, t) & :=frac{w}{2}(f(x(t))-c) \ rho^{w}(x, f(x)<c, t) & :=frac{w}{2}(c-f(x(t))) \ rho^{w}(x, neg varphi, t) & :=-rho^{w}(x, varphi, t) \ rho^{w}left(x, wedge_{i=1: N}^{w} varphi_{i}, tright) & :=g^{wedge}left(w,left[rho^{w}left(x, varphi_{i}, tright)right]_{i=1: N}right) \ rho^{w}left(x, vee_{i=1: N}^{w} varphi_{i}, tright) & :=g^{vee}left(w,left[rho^{w}left(x, varphi_{i}, tright)right]_{i=1: N}right) \ rho^{w}left(x, square_{left[tau_{1}, tau_{2}right]}^{w} varphi, tright) & :=g^{square}left(w,left[rho^{w}(x, varphi, t)right]_{t^{prime} inleft[t+tau_{1}, t+tau_{2}right]}right) \ rho^{w}left(x, diamond_{left[tau_{1}, tau_{2}right]} varphi, tright) & :=g^{diamond}left(w,left[rho^{w}(x, varphi, t)right]_{t^{prime} inleft[t+tau_{1}, t+tau_{2}right]}right)end{array} ρw(x,f(x)≥c,t)ρw(x,f(x)<c,t)ρw(x,¬φ,t)ρw(x,∧i=1:Nwφi,t)ρw(x,∨i=1:Nwφi,t)ρw(x,□[τ1,τ2]wφ,t)ρw(x,⋄[τ1,τ2]φ,t):=2w(f(x(t))−c):=2w(c−f(x(t))):=−ρw(x,φ,t):=g∧(w,[ρw(x,φi,t)]i=1:N):=g∨(w,[ρw(x,φi,t)]i=1:N):=g□(w,[ρw(x,φ,t)]t′∈[t+τ1,t+τ2]):=g⋄(w,[ρw(x,φ,t)]t′∈[t+τ1,t+τ2])
- 对于形如 f ( x ) > c f(x)>c f(x)>c或 f ( x ) < c f(x)<c f(x)<c的一阶命题, 加权鲁棒度的权重是给定权值 w w w的一半(咱也不知道为什么这么定义).
- 对于逻辑操作子, 针对不同的原子命题的权重进行激活
- 对于时序操作子, 针对不同时刻的权重进行激活
Activation function
Υ = ( g ∧ , g ∨ , g □ , g ⋄ ) Upsilon=left(g^{wedge}, g^{vee}, g^{square}, g^{diamond}right) Υ=(g∧,g∨,g□,g⋄)根据权重激活STL式子中的子公式, 具体函数在后面进行定义。
3 Temporal Logic Neural Network
作者用下面这个神经网络 (TLNN) 完成了信号鲁棒度的计算. 输入的是一个多维信号, 输出是wSTL的鲁棒度.
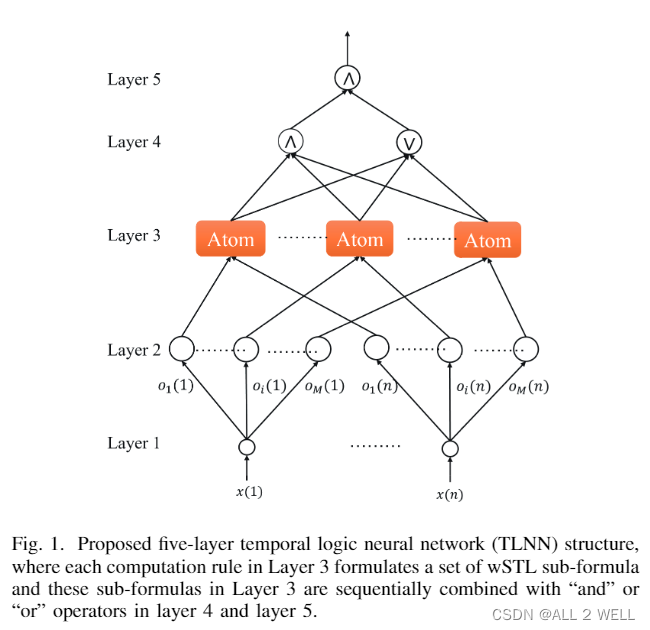
接下来介绍每一层干了什么:
前情提要: M = d i m ( x ) × 4 M=dim(x)times 4 M=dim(x)×4, 代表每条通道的4条一阶、二阶公式组合
| L1 | L2 | L3 | L4 | L5 | |
|---|---|---|---|---|---|
| 神经元个数 | 信号采样点的个数 n n n | n × M n times M n×M | 模板数 M M M | 2: and和or | 1个and神经元 |
| 单神经元输入 | t t t时刻信号值 | 某时刻信号值 | μ i ( t ) mu_i(t) μi(t) | M M M个候选公式的鲁棒度 | and和or组合的鲁棒度 ρ 4 rho^4 ρ4 |
| 单神经元输出 | M个值, o i ( t ) , . . . , o M ( t ) o_i(t),..., o_M(t) oi(t),...,oM(t), o i ( t ) o_i(t) oi(t)表示第 t t t时刻对应的神经元的第 i i i个输出, 分别对应M个候选公式 (不包含任何操作子的最简形式, 因此可以推测 M = d i m ( x ) × 4 M=dim(x)times 4 M=dim(x)×4) | 零阶命题的鲁棒度 μ i ( t ) mu_i(t) μi(t),即 ρ i 2 , 1 = 1 : n rho_i^2,1=1:n ρi2,1=1:n | 简单公式的鲁棒度 ρ i 3 , i = 1 : M rho_i^3,i=1:M ρi3,i=1:M | and或or组合后的鲁棒度 ρ 4 rho^4 ρ4 | and组合后的鲁棒度 |
| 待学习参数 | 无参数 | 向量 W 1 = [ W 1 1 , W 2 1 , . . . , W M 1 ] W^1=[W^1_1, W^1_2,...,W^1_M] W1=[W11,W21,...,WM1] (STL尺度参数) | θ e , θ d , [ τ 1 , τ 2 ] , W 2 theta_e,theta_d,[tau_1,tau_2],W^2 θe,θd,[τ1,τ2],W2 | W 3 W^3 W3各模板的组合权重 | W 4 W^4 W4组合权重 |
Layer 1 (Input layer)
这一层可以看作一个数据分发器. 把 t t t时刻的信号复制 M M M份分发给不同的代选公式中.
Layer 2 (Predicate layer)
第二层计算最简公式(零阶命题)的加权鲁棒度.
每个神经元代表一个命题, 调用
ρ
i
2
=
μ
i
(
t
)
=
f
(
x
(
t
)
)
−
W
i
1
rho^2_i=mu_i(t)=f(x(t))-W^1_i
ρi2=μi(t)=f(x(t))−Wi1计算鲁棒度序列, 由此式可以看出,这一层神经元的待学习参数
W
1
=
[
W
1
1
,
W
2
1
,
.
.
.
,
W
M
1
]
W^1=[W^1_1,W^1_2,...,W^1_M]
W1=[W11,W21,...,WM1]分别为
M
M
M个公式模板中的STL的尺度参数。
Layer 3 (Atomic formula layer)
在这一层计算一阶、二阶的鲁棒度,通过时序操作子将 M M M个零阶公式的鲁棒度序列组合起来。
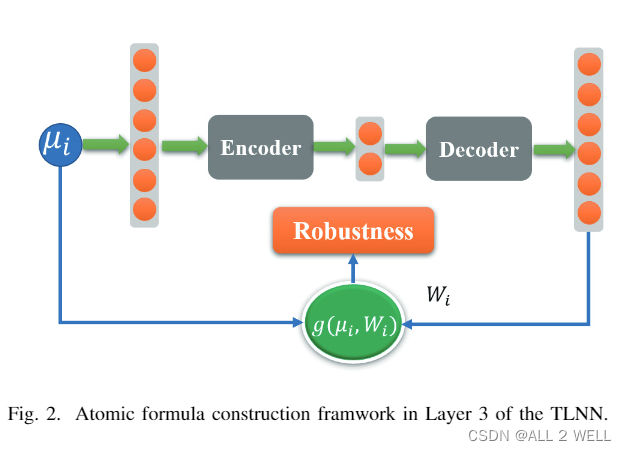
此层的神经元结构如上图所示.
Auto-Encoder
为什么要这样先编码再解码呢?是不是多此一举?这里这个结构叫做自编码器(Auto-Encoder)。
Encoder的作用是把输入的高维鲁棒度序列 ρ i 2 rho^2_i ρi2先转化为隐变量 h h h, decoder的作用是把 h h h还原到原始的维度, 传统的AE希望输出能够与输入近似。
这是在干什么呢?可以想象这个神经网络通过自己的消化理解后,找到输入的内在规律后,将输入的序列背诵了出来。根据正常数据训练出来的Autoencoder,能够将正常样本重建还原,但是却无法将异常分布的数据点较好地还原,导致还原误差较大。在时间序列异常检测场景下,如果自编码器无法还原正确还原输入,则说明输入的时间序列存在异常。
但是这篇文章中AE的作用比较牵强,并不是向上面一样进行异常检测,而是强行训练出信号点的权重时间序列。强行把自编码器的隐变量解释为时间参数 [ τ 1 , τ 2 ] [tau_1,tau_2] [τ1,τ2]。
在解码之前,AE还对隐变量 h h h进行了进一步操作, 将其转换为我们想要得到的时间参数 τ 1 , τ 2 tau_1,tau_2 τ1,τ2。文中称这个过程为量化,方便最后能够直接读出时间参数。其过程如下:
对
h
1
,
h
2
h_1,h_2
h1,h2进行量化 (转化成整数序号),其中
△
triangle
△是量化阶梯的长度。
Q
(
x
)
=
{
l
x
<
l
u
x
>
u
l
+
Δ
(
i
+
κ
(
x
)
+
1
2
)
x
∈
P
i
Q(x)=left{ begin{array}{cl} l & x<l \ u & x>u \ l+Delta(i+frac{kappa(x)+1}{2}) & xinmathcal{P_i} \ end{array} right.
Q(x)=⎩⎨⎧lul+Δ(i+2κ(x)+1)x<lx>ux∈Pi
当然需要保证计算过程可导, 其中 k k k是一个超参数, 决定阶梯的平滑程度.
κ ( x ) = 1 t a n h ( 0.5 k △ ) t a n h ( k ( x − l − ( i + 0.5 ) △ ) ) kappa(x)=frac{1}{tanh(0.5ktriangle)tanh(k(x-l-(i+0.5)triangle))} κ(x)=tanh(0.5k△)tanh(k(x−l−(i+0.5)△))1
Activation Function
说完了自编码器的作用,接下来将 g ( μ i , W i ) g(mu_i,W_i) g(μi,Wi)函数的作用。这个函数被称为激活函数(Activation Function)。四种公式模板对应4种神经元,需要分别编写激活函数。
论文中将自编码器的输出作为时序权重来计算鲁棒度序列 μ i mu_i μi即 ρ i 2 rho^2_i ρi2相对于简单公式模板的鲁棒度。
怎么理解这一步激活呢?文中的写法有点问题,这里应该就是求第一步中得到的鲁棒度序列的最大最小值了。更正后如下:
1. always
g
□
(
ρ
2
,
W
2
)
=
ρ
ω
(
x
,
□
[
τ
1
,
τ
2
]
W
2
φ
i
,
t
)
g^square(rho^2,W^2)=rho^omega(x,square^{W^2}_{[tau_1,tau_2]}varphi_i,t)
g□(ρ2,W2)=ρω(x,□[τ1,τ2]W2φi,t)
2. eventually
g
⋄
(
ρ
2
,
W
2
)
=
ρ
ω
(
x
,
⋄
[
τ
1
,
τ
2
]
W
2
φ
i
,
t
)
g^diamond(rho^2,W^2)=rho^omega(x,diamond^{W^2}_{[tau_1,tau_2]}varphi_i,t)
g⋄(ρ2,W2)=ρω(x,⋄[τ1,τ2]W2φi,t)
3. eventually always
对于含有两个时序算子的,激活函数复杂一些,但是这里依然只要有两个时间参数
τ
1
,
τ
2
tau_1,tau_2
τ1,τ2,
τ
0
tau_0
τ0是写死的。
g
□
⋄
(
ρ
i
2
,
W
2
)
=
ρ
ω
(
x
,
∧
j
=
0
:
τ
0
⋄
[
τ
1
+
j
,
τ
2
+
j
]
W
2
φ
i
,
t
)
g^{squarediamond}(rho^2_i,W^2)=rho^{omega}(x,land_{j=0:tau_0}diamond^{W^2}_{[tau_1+j,tau_2+j]}varphi_i,t)
g□⋄(ρi2,W2)=ρω(x,∧j=0:τ0⋄[τ1+j,τ2+j]W2φi,t)
4. always eventually
g
⋄
□
(
ρ
i
2
,
W
2
)
=
ρ
ω
(
x
,
∨
j
=
0
:
τ
0
□
[
τ
1
+
j
,
τ
2
+
j
]
W
2
φ
i
,
t
)
g^{diamondsquare}(rho^2_i,W^2)=rho^{omega}(x,lor_{j=0:tau_0}square^{W^2}_{[tau_1+j,tau_2+j]}varphi_i,t)
g⋄□(ρi2,W2)=ρω(x,∨j=0:τ0□[τ1+j,τ2+j]W2φi,t)
为了保证每一步可导,这里当然也需要平滑化处理,文章用的平滑方法为arithmetric-geometric integral mean
min ~ { [ x 1 , x 2 , . . . , x N ] } = { [ Π i = 1 : N ( 1 + x i ) ] 1 N − 1 ∀ x i > 0 , i = 1 , . . . , n 1 N ∑ i = 1 : N [ x i ] − o t h e r w i s e tilde{min}{[x_1,x_2,...,x_N]}=left{ begin{array}{cl} [Pi_{i=1:N}(1+x_i)]^{frac{1}{N}}-1 & forall x_i>0,i=1,...,n \ frac{1}{N} sum_{i=1:N}[x_i]_- & otherwise\ end{array} right. min~{[x1,x2,...,xN]}={[Πi=1:N(1+xi)]N1−1N1∑i=1:N[xi]−∀xi>0,i=1,...,notherwise
其中otherwise部分表示:如果存在负值,那最小值肯定是负值,则把正值清零,计算平均值
max ~ { [ x 1 , x 2 , . . . , x N ] } = { 1 − [ Π i = 1 : N ( 1 − x i ) ] 1 N ∀ x i < 0 , i = 1 , . . . , n 1 N ∑ i = 1 : N [ x i ] + o t h e r w i s e tilde{max}{[x_1,x_2,...,x_N]}=left{ begin{array}{cl} 1-[Pi_{i=1:N}(1-x_i)]^{frac{1}{N}} & forall x_i<0,i=1,...,n \ frac{1}{N} sum_{i=1:N}[x_i]_+ & otherwise\ end{array} right. max~{[x1,x2,...,xN]}={1−[Πi=1:N(1−xi)]N1N1∑i=1:N[xi]+∀xi<0,i=1,...,notherwise
其中otherwise部分表示:如果存在正值,那最大值肯定是负值,则把负值清零,计算平均值。
Layer 4 (Formula reduction layer)
第4层通过布尔操作子将上面的四种子公式组合起来。
这一层只有两个神经元,一个是and神经元,一个是or神经元
分别把L3中的M个结果加权求最大最小。
Layer 5 (Output layer)
第五层输出最终and加权组合下的公式。
4 TLNN Learning
A. Structure learning
这里补充说明到, M M M的数量并不是事先指定的,而是动态增加的。但是在论文这个框架下是大可不必啊,因为最多也就4种模板。
Neuron reduction
如果某个模板公式的权重太低了,就将其置零。
这一步并不可导,所以推测是最后读取的时候才进行。
Neuron increase
如果最终的鲁棒度输出太离谱了,就在L3增加一个神经元(即增加一种模板),神经元类型为上面4种中随机一种。
这一步就黑人问号??:
- 这一步判断实在什么时候进行?如果每次BP都进行一次,那么初期网络岂不是会疯狂生长??如果有模板数量有上限的话,网络会瞬间增长到最大。这样还不如直接固定好模板数,毕竟不多。
- 结果不满意继续训练权重就好了,为什么要增加一个一样的神经元重新训练??
B. Parameter Learning
神经网络优化的是输出鲁棒度于理想鲁棒度的差异
L = 1 2 ( y − y d ) 2 L=frac{1}{2}(y-y_d)^2 L=21(y−yd)2
接下来讲的是反向传播是如何进行链式求导的,没什么创新点,这里就不展开。
最后又发现一个矛盾点:
前面的模板中并没有零阶公式为 x < W i x<W^i x<Wi这个选项,但是这里说 ∂ ρ i 2 , j ∂ W j 1 frac{partial rho_i^{2,j}}{partial W^1_j} ∂Wj1∂ρi2,j能够取 ± 1 pm1 ±1,应该是原作者欠考虑了。
5 Case Studies
背景介绍
实验基于轴承的异常诊断场景,异常数据通过在轴承特定部位上刻蚀一条小缝产生。原始数据还进行了小波变换等一系列处理。

结果
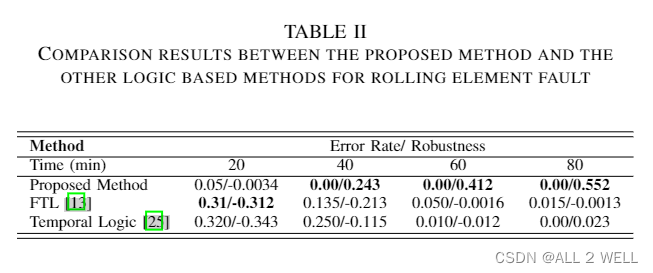
结果并没有反映出学习出来的权重,wSTL到STL之间怎么进行转换的不得而知。
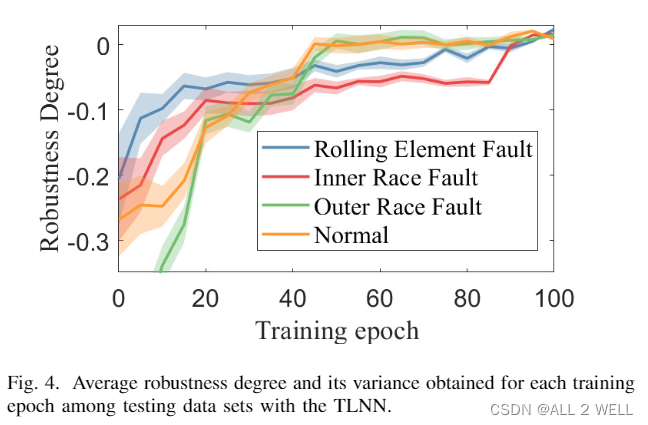
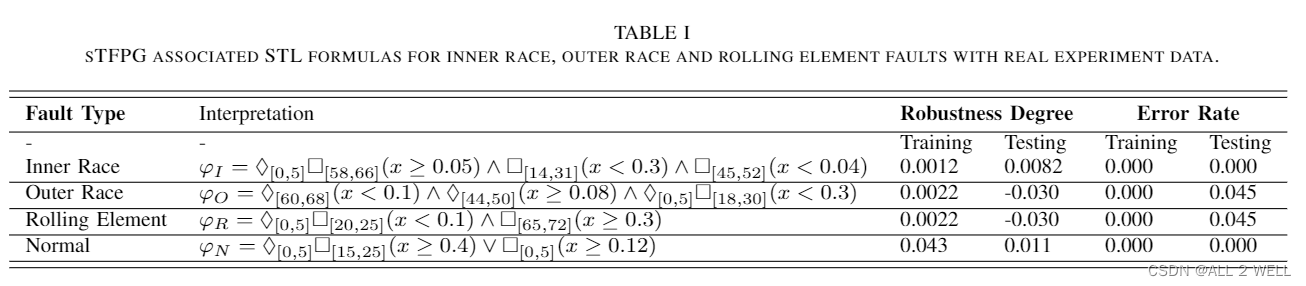
最后还和其他的方法做了对比,结果如下。
6 Conclusions
创新点:
- 结合了神经网络
- 用真实数据集进行了实验
心得与记录
- 这篇文章比较很多,写得比较乱,请读者谅解
- 论文没有交代清楚自编码器的作用,也没有交代清楚wSTL到STL的转换关系
最后
以上就是懵懂小白菜最近收集整理的关于【论文精读】时序逻辑推理之时序神经网络 Interpretable Fault Diagnosis of Rolling Element Bearings with TLNN概览流水账笔记心得与记录的全部内容,更多相关【论文精读】时序逻辑推理之时序神经网络内容请搜索靠谱客的其他文章。








发表评论 取消回复