概述
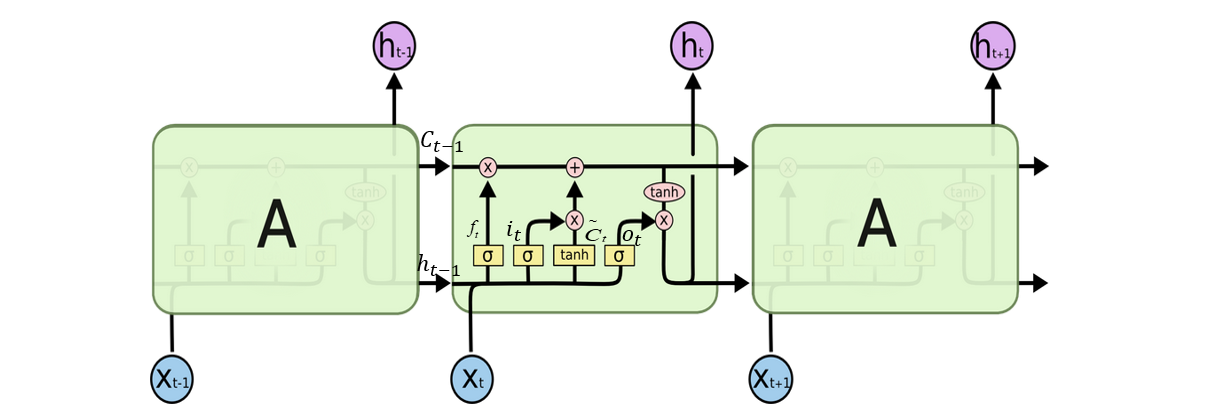
这是一张经典的LSTM示意图，LSTM依靠
f
t
f_t
ft、
i
t
i_t
it、
o
t
o_t
ot来控制输入输出，
f
t
=
σ
(
W
f
⋅
[
h
t
−
1
,
x
t
]
+
b
f
)
f_{t}=sigmaleft(W_{f} cdotleft[h_{t-1}, x_{t}right]+b_{f}right)
ft=σ(Wf⋅[ht−1,xt]+bf)
i
t
=
σ
(
W
i
⋅
[
h
t
−
1
,
x
t
]
+
b
i
)
i_{t}=sigmaleft(W_{i} cdotleft[h_{t-1}, x_{t}right]+b_{i}right)
it=σ(Wi⋅[ht−1,xt]+bi)
o
t
=
σ
(
W
o
[
h
t
−
1
,
x
t
]
+
b
o
)
o_{t}=sigmaleft(W_{o}left[h_{t-1}, x_{t}right]+b_{o}right)
ot=σ(Wo[ht−1,xt]+bo)
我们将其简化为：
f
t
=
σ
(
W
f
X
t
+
b
f
)
f_{t}=sigmaleft(W_{f} X_{t}+b_{f}right)
ft=σ(WfXt+bf)
i
t
=
σ
(
W
i
X
t
+
b
i
)
i_{t}=sigmaleft(W_{i} X_{t}+b_{i}right)
it=σ(WiXt+bi)
o
i
=
σ
(
W
o
X
t
+
b
o
)
o_{i}=sigmaleft(W_{o} X_{t}+b_{o}right)
oi=σ(WoXt+bo)
当前的状态
S
t
=
f
t
S
t
−
1
+
i
t
X
t
S_{t}=f_{t} S_{t-1}+i_{t} X_{t}
St=ftSt−1+itXt 类似与传统RNN
S
t
=
W
s
S
t
−
1
+
W
x
X
t
+
b
1
S_{t}=W_{s} S_{t-1}+W_{x} X_{t}+b_{1}
St=WsSt−1+WxXt+b1 。将LSTM的状态表达式展开后得：
S
t
=
σ
(
W
f
X
t
+
b
f
)
S
t
−
1
+
σ
(
W
i
X
t
+
b
i
)
X
t
S_{t}=sigmaleft(W_{f} X_{t}+b_{f}right) S_{t-1}+sigmaleft(W_{i} X_{t}+b_{i}right) X_{t}
St=σ(WfXt+bf)St−1+σ(WiXt+bi)Xt 如果加上激活函数
S
t
=
tanh
[
σ
(
W
f
X
t
+
b
f
)
S
t
−
1
+
σ
(
W
i
X
t
+
b
i
)
X
t
]
S_{t}=tanh left[sigmaleft(W_{f} X_{t}+b_{f}right) S_{t-1}+sigmaleft(W_{i} X_{t}+b_{i}right) X_{t}right]
St=tanh[σ(WfXt+bf)St−1+σ(WiXt+bi)Xt] RNN梯度消失和爆炸的原因这篇文章中传统RNN求偏导的过程包含：
∏
j
=
k
+
1
t
∂
S
j
∂
S
j
−
1
=
∏
j
=
k
+
1
t
tanh
′
W
s
prod_{j=k+1}^{t} frac{partial S_{j}}{partial S_{j-1}}=prod_{j=k+1}^{t} tanh ^{prime} W_{s}
j=k+1∏t∂Sj−1∂Sj=j=k+1∏ttanh′Ws 对于LSTM同样也包含这样的一项，但是在LSTM中：
∏
j
=
k
+
1
t
∂
S
j
∂
S
j
−
1
=
∏
j
=
k
+
1
t
tanh
′
σ
(
W
f
X
t
+
b
f
)
prod_{j=k+1}^{t} frac{partial S_{j}}{partial S_{j-1}}=prod_{j=k+1}^{t} tanh ^{prime} sigmaleft(W_{f} X_{t}+b_{f}right)
j=k+1∏t∂Sj−1∂Sj=j=k+1∏ttanh′σ(WfXt+bf) 假设
Z
=
tanh
′
(
x
)
σ
(
y
)
Z=tanh ^{prime}(x) sigma(y)
Z=tanh′(x)σ(y)，则
Z
Z
Z的函数图像如下图所示：
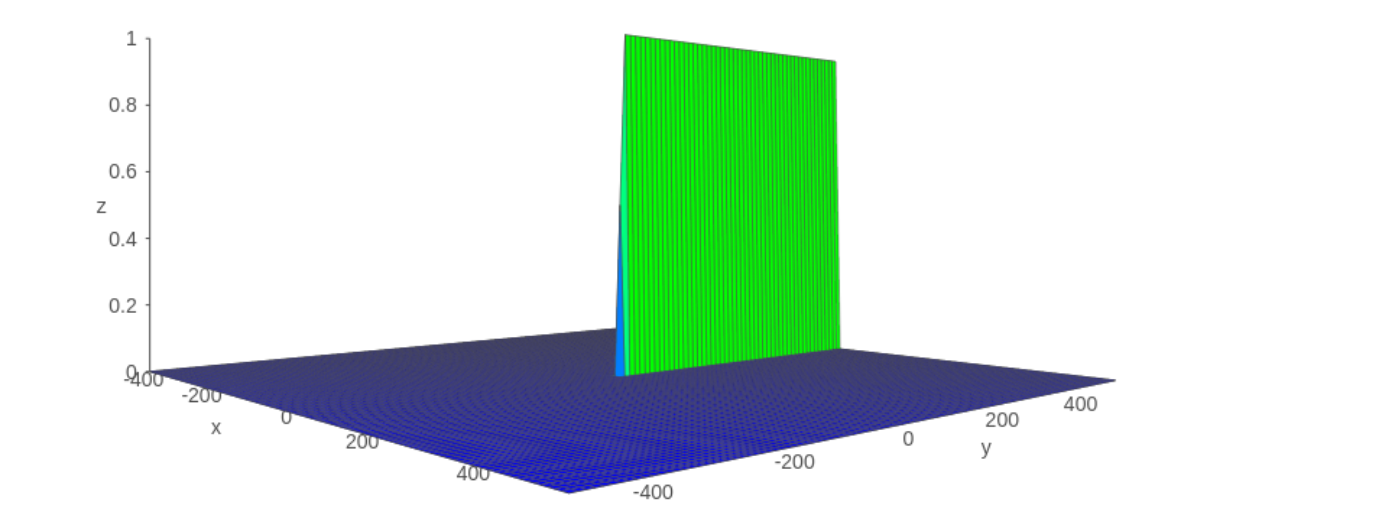
可以看到该函数值基本上不是0就是1。
传统RNN的求偏导过程：
∂
L
3
∂
W
s
=
∂
L
3
∂
O
3
∂
O
3
∂
S
3
∂
S
3
∂
W
s
+
∂
L
3
∂
O
3
∂
O
3
∂
S
3
∂
S
3
∂
S
2
∂
S
2
∂
W
s
+
∂
L
3
∂
O
3
∂
O
3
∂
S
3
∂
S
3
∂
S
2
∂
S
2
∂
S
1
∂
S
1
∂
W
s
frac{partial L_{3}}{partial W_{s}}=frac{partial L_{3}}{partial O_{3}} frac{partial O_{3}}{partial S_{3}} frac{partial S_{3}}{partial W_{s}}+frac{partial L_{3}}{partial O_{3}} frac{partial O_{3}}{partial S_{3}} frac{partial S_{3}}{partial S_{2}} frac{partial S_{2}}{partial W_{s}}+frac{partial L_{3}}{partial O_{3}} frac{partial O_{3}}{partial S_{3}} frac{partial S_{3}}{partial S_{2}} frac{partial S_{2}}{partial S_{1}} frac{partial S_{1}}{partial W_{s}}
∂Ws∂L3=∂O3∂L3∂S3∂O3∂Ws∂S3+∂O3∂L3∂S3∂O3∂S2∂S3∂Ws∂S2+∂O3∂L3∂S3∂O3∂S2∂S3∂S1∂S2∂Ws∂S1
在LSTM中为：
∂
L
3
∂
W
s
=
∂
L
3
∂
O
3
∂
O
3
∂
S
3
∂
S
3
∂
W
s
+
∂
L
3
∂
O
3
∂
O
3
∂
S
3
∂
S
2
∂
W
s
+
∂
L
3
∂
O
3
∂
O
3
∂
S
3
∂
S
1
∂
W
s
frac{partial L_{3}}{partial W_{s}}=frac{partial L_{3}}{partial O_{3}} frac{partial O_{3}}{partial S_{3}} frac{partial S_{3}}{partial W_{s}}+frac{partial L_{3}}{partial O_{3}} frac{partial O_{3}}{partial S_{3}} frac{partial S_{2}}{partial W_{s}}+frac{partial L_{3}}{partial O_{3}} frac{partial O_{3}}{partial S_{3}} frac{partial S_{1}}{partial W_{s}}
∂Ws∂L3=∂O3∂L3∂S3∂O3∂Ws∂S3+∂O3∂L3∂S3∂O3∂Ws∂S2+∂O3∂L3∂S3∂O3∂Ws∂S1
因为
∏
j
=
k
+
1
t
∂
S
j
∂
S
j
−
1
=
∏
j
=
k
+
1
t
tanh
′
σ
(
W
f
X
t
+
b
f
)
≈
0
∣
1
prod_{j=k+1}^{t} frac{partial S_{j}}{partial S_{j-1}}=prod_{j=k+1}^{t} tanh ^{prime} sigmaleft(W_{f} X_{t}+b_{f}right) approx 0 | 1
j=k+1∏t∂Sj−1∂Sj=j=k+1∏ttanh′σ(WfXt+bf)≈0∣1
这样就解决了传统RNN中梯度消失的问题。
最后
以上就是潇洒小蚂蚁为你收集整理的LSTM如何解决梯度消失与梯度爆炸的全部内容，希望文章能够帮你解决LSTM如何解决梯度消失与梯度爆炸所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
![[rnn]BPTT_梯度消失/爆炸问题](/uploads/reation/bcimg8.png)
发表评论 取消回复