任意阶球谐函数可视化

69 阅读 0 评论 46 点赞

我是靠谱客的博主贤惠心情，最近开发中收集的这篇文章主要介绍任意阶球谐函数可视化，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

先上效果图。从上到下依次为n=0:5, 从左到右依次为m=0:5, n代表阶，m代表级。

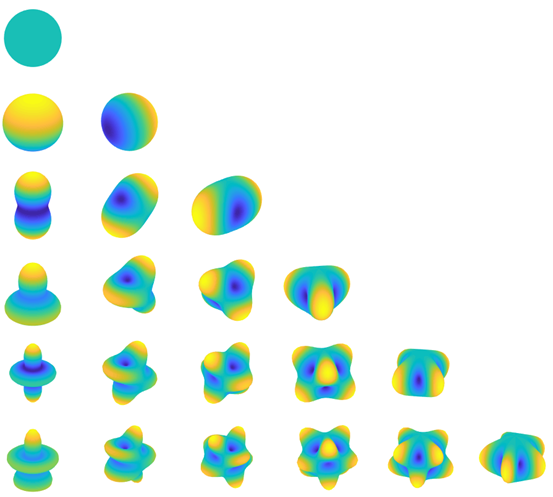
上图的颜色代表的就是球谐函数的取值（后续我会把解析公式放上来），但是半径却是加工过的（具体参考下面的代码）。如果把半径设为球谐函数的绝对值，如下图所示

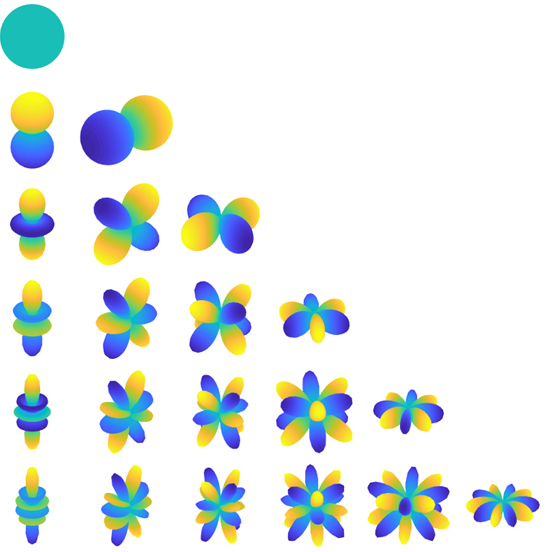
不再过多解释，下面给出matlab制图代码

% 绘制球谐函数图像
% degree, Ynm的n, 阶
% order,  Ynm的m, 级
% method, 绘图的R
%% 示例 - 绘制球谐函数表
% maxD = 3; % 最高阶数
% for n = 0:maxD
%     for m = 0:n
%         subplot(maxD+1,maxD+1,n*(maxD+1)+m+1)
%         plot_sph_harm(n,m,2);
%     end
% end
function plot_sph_harm(degree,order,method)
    %% 坐标
    theta = 0:pi/30:pi;                   % polar angle
    phi = 0:pi/30:2*pi;                   % azimuth angle
    [phi,theta] = meshgrid(phi,theta);    % define the grid
    
    %% 计算球谐函数
    Ln = legendre(degree,cos(theta(:,1)),'norm');     % 一行对应一个order
    yy = repmat(Ln(order+1,:)',[1,size(theta,2)]); % Ln(i+1,:)对应order=i
    Ynm = yy.*cos(order*phi);                % 球谐函数, 相当于绘图的color
    
    %% R的选择
    if nargin < 3, method = 1; end
    switch method
        case 1
            R = ones(size(phi));      % 绘制在单位球上
        case 2
            R = abs(Ynm) + 0.2;       % 与color一致
        case 3
            R = Ynm*0.4 + 1;          % 看上去像单位球发生了形变
        case 4
            % 来自Help文档'Animating a Surface'
            R = 5 + 0.5*Ynm/max(max(abs(Ynm)));  
            % radius = 5; amplitude = 0.5;
        otherwise
            error('[ERROR] -- 没有该方案，请检查 methodn')
    end

    %% 转化为直角坐标
    Rxy = R.*sin(theta);    % convert to Cartesian coordinates
    x = Rxy.*cos(phi);
    y = Rxy.*sin(phi);
    z = R.*cos(theta);
    
    %% 绘图方案1 (注:将坐标调稠密一些更好看)
    surf(x,y,z,Ynm,'edgecolor','none','facecolor','interp');
    axis equal off     % set axis equal and remove axis
    colormap parula;
    material shiny;
    camzoom(1.5)        % zoom into scene
    %% 绘图方案2 (注:将坐标调稀疏一些更好看)
%     surf(x,y,z,Ynm);
%     light               % add a light
%     lighting gouraud    % preferred lighting for a curved surface
%     axis equal off      % set axis equal and remove axis
%     view(40,30)         % set viewpoint
%     camzoom(1.5)        % zoom into scene

end