从3G到今天的5G,数据信道的调制方式越多也相对复杂

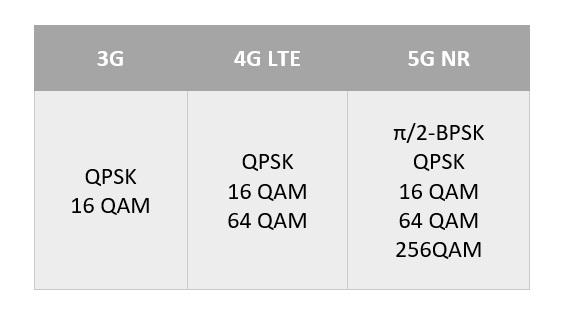
图1 3G-5G的调制演进

这幅图中，BPSKQPSK叫做二进制正交相移键控，是把模拟信号转换成数据值的转换方式之一；QAM叫做正交振幅调制。这些调制方法已经用到了5G数据信道上(PUSCH/PDSCH)了，班长会在后续的文章中与大家分享。

图2 5G时代来临

今天分享的内容：IQ调制

因为，现代通信中，IQ调制基本上属于是标准配置，因为利用IQ调制可以做出所有的调制方式。所以说掌好IQ调制，后面的其他调制方法与5G学习将不在话下。

IQ调制

IQ调制其实很简单，直接给出：

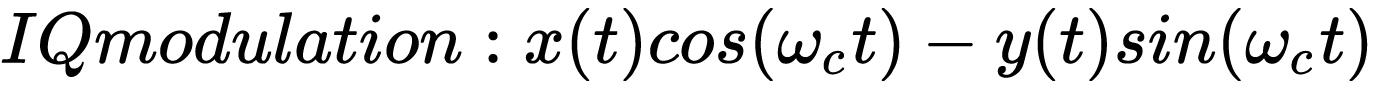
其中I路的信号为x(t)cos，Q路的信号为y(t)sin。

再看下整个玩意是否容易解调恢复出来呢，接收端先乘以余弦cos(wct)

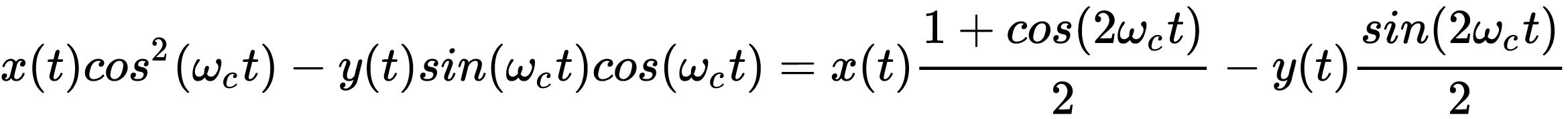
再乘以-sin(wct)

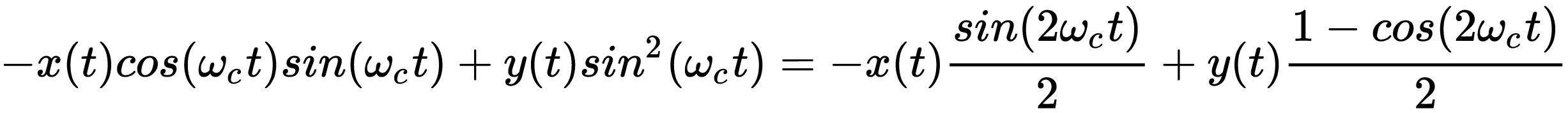
通过低通滤波器，我们都可以把2倍频率滤除，得到x(t)和y(t)。

我们把cos定义为参考相位，如果相对于参考相位，相位为零，这样的载波就是In-phase，就像上文中的coswct；相对于参考相位，相位有-90度的差，这样的载波就是Quadrature phase，就像上文中的sinwct。

要传递的信号分成了两个部分，分别加载在这两个载波的振幅上面。最后，把两个调制信号加起来，就得到了一个新的信号。

与SSB的关系

AM、DSB、SSB这些调制方式，均是在频域内将原始的基带频谱搬移到载波频率处，仅仅是传输效率不同。其中单边带信号SSB，只需要一个子边带便可以实现无损失的传输。

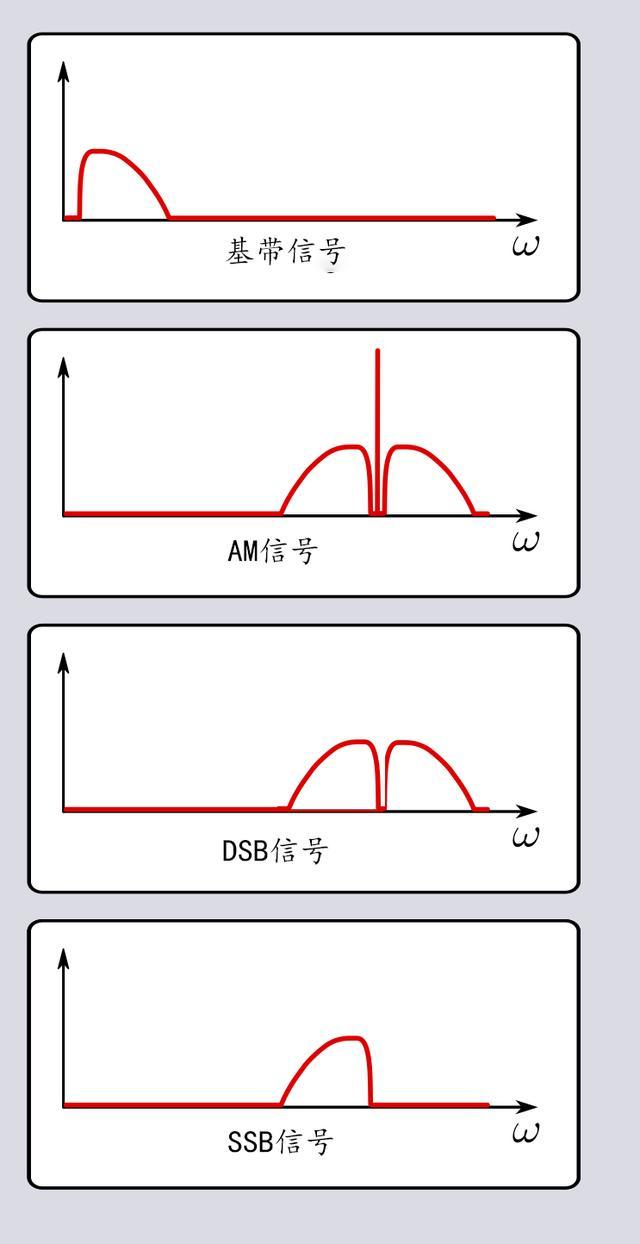
图3 各种调制信号

作为代价，SSB信号的时域表达式有些复杂

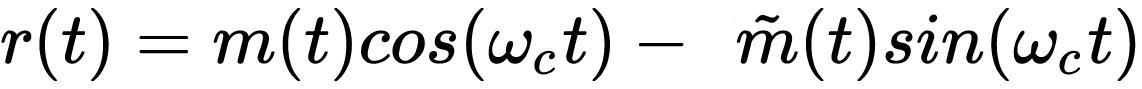
其中m(t)是调制信号，m~(t)信号是其Hilbert变换。

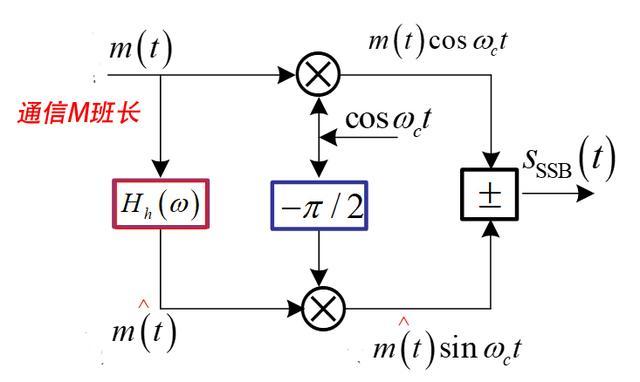
图4 SSB信号的产生

其实IQ调制，就是把m(t)和m~(t)信号替换成x(t)和y(t)信号，这样我们就可以同时传输两路信号了！

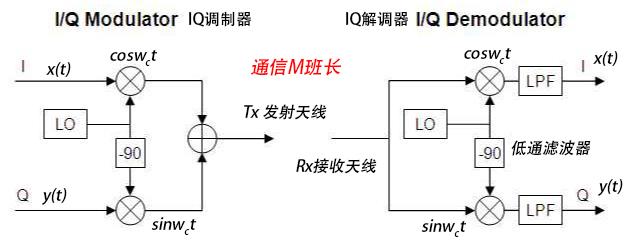
图5 IQ信号产生与接收

复数信号

上面的这个信号，看起来和复数毫无关系！但是我们可以这样谢

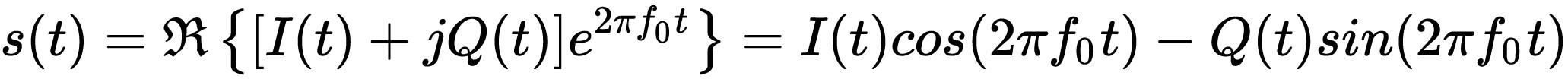
这个IQ信号，可以看成是一个基带复数信号(I+jQ)，乘上一个复指数信号(复载波)，就得到了复调制信号。对这个复调制信号取实数部分，就得到了IQ调制信号了。

在信号处理中，前辈们都说复数信号看起来更加简洁便利。

所以会把传递过来的两路信号，拼接到一起，组成一个复数。但实际的传播过程，只能传输实际物理信号，也需要取其实数部分。

看起来很乱。因为这里涉及到内容很多，如果有基带调制、射频调制的基础，看起来会好一些。后续班长会和大家聊一聊基带、射频，当你积累了一定的知识之后，再回头总结，会别有一番风味。

图6 学习贵在坚持

关于拼接、分解信号，以及会在频谱上造成如何变化

先看下我们熟悉的cos和sin信号，根据欧拉公式，我们可以得出：

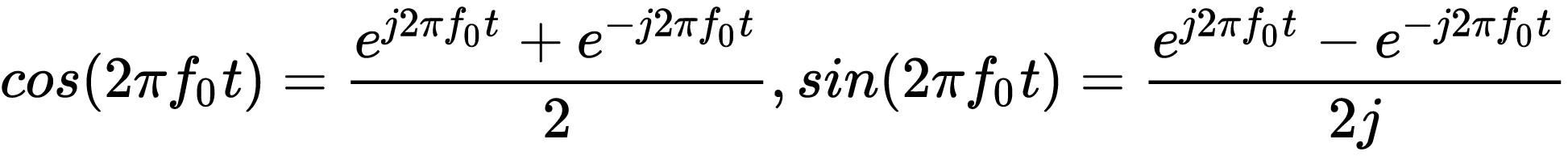
我们知道余弦和正弦的傅里叶变换(这个变换理工科应该背下来，这是基础公式，证明过程也不是很难)是冲激函数

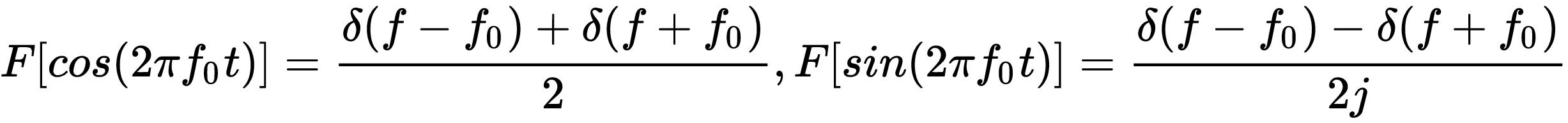
国内的教材大多在二维图像上观看频谱，这里我们在实数轴、频率轴和虚数轴组成的三维坐标系内，画出频谱：

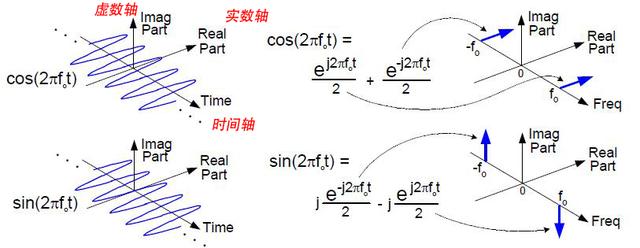
图7 sin和cos三维频谱图

我们用j乘以sin(2πf0t)，然后再与cos(2πf0t)相加，得出的新的频谱恰巧是e^j2πf0t的频谱。看到没，复数信号的频谱就是比实数信号简洁吧，只有正频率。

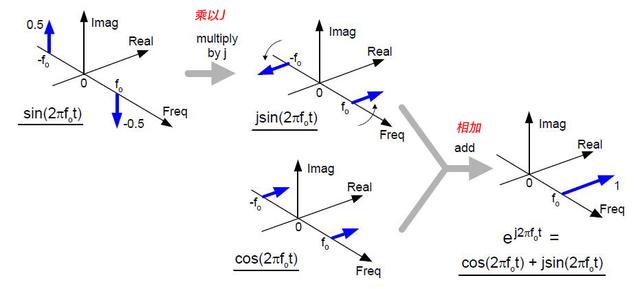
图8 复指数函数的频谱

我们把实数轴定义为同相(In-phase)分量，虚数轴定义为正交(quadrature)分量。这样复平面我们可以叫做IQ平面了。

接下里，我们尝试画出cos(2πf0t+Φ)的频谱，先用和差公式分解

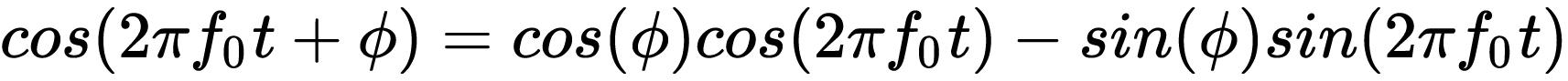
然后取傅里叶变换

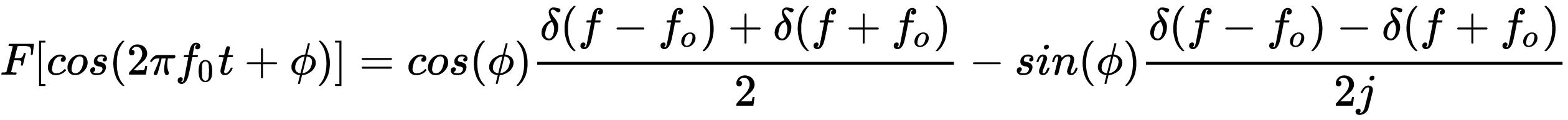
图9a，cos(2πf0t+Φ)可以分解成IQ，每路分量别振幅由cosΦ和sinΦ调制。图9b是6个cos(2πf0t+Φ)累加后的频谱波形，图9c是无数个cos(2πf0t+Φ)波形累加(我们知道无数个正弦函数累加，可以得到方波脉冲)，图9d是对应的复数信号频谱，只有正频率分量。

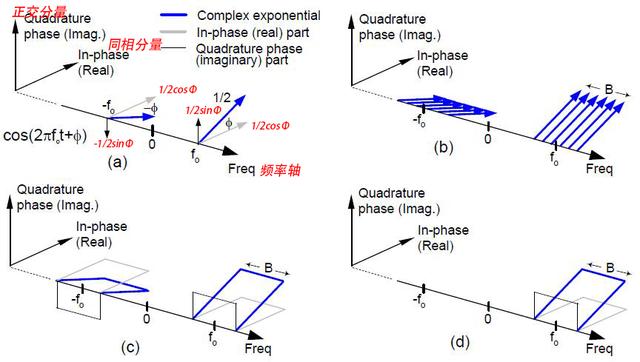
图9 实数信号频谱

通过观察上述几幅图，我们直观的感受到：

实数信号通常有正、负频率分量，并且在同相In-phase分量上，正频率分量和负频率分量是关于零频率偶对称的。也就是说，在同相In-phase分量上,正负频率互成镜像。与此相反，在正交分量Quadrature中，正和负频率分量互为相反，也就是说正频率与负频率的相位角互为相反数。但不管是同相分量(也就是Real实数轴)，还是正交分量Quadrature(Img虚数轴)，我们都可以称之为共轭对称，因为实数的共轭就是其本身。

这里，还有一个重要的性质，就是傅里叶的频移特性：

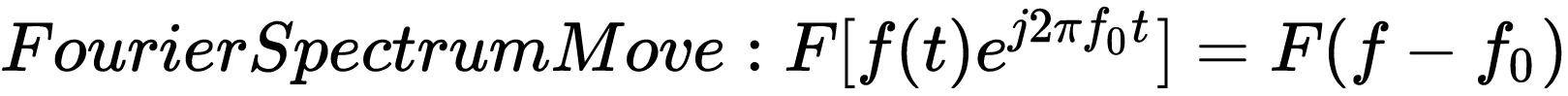
如下图10所示，当时域信号乘以复指数信号e^2πf0t，频谱向正频率方向搬移f0;当时域信号乘以复指数信号e^-2πf0t，频谱向负频率方向搬移f0；

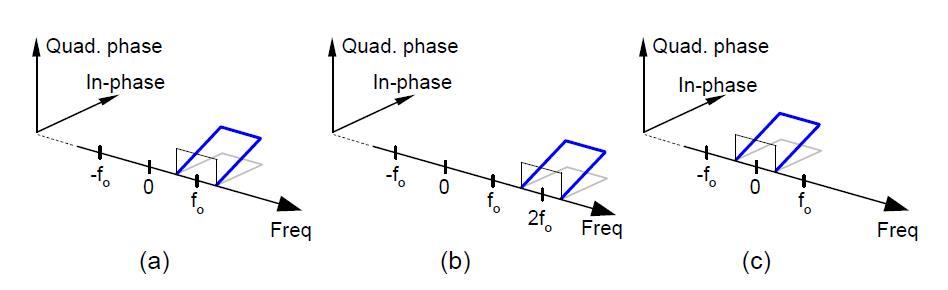
图10 傅里叶频域移动性质

比如对一个带通信号Xbp(f)，其频谱为图11第一排所示，正负频率都有频谱分量。其同相频谱为第二排图形，乘以cos，频谱左右搬移。然后经过低通滤波器，滤除倍频部分。

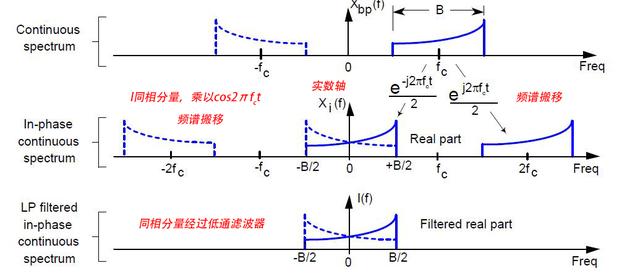
图11 同相分量

其正交频谱为图12第二排图形，乘以sin，频谱左右搬移。然后经过低通滤波器，滤除倍频部分。

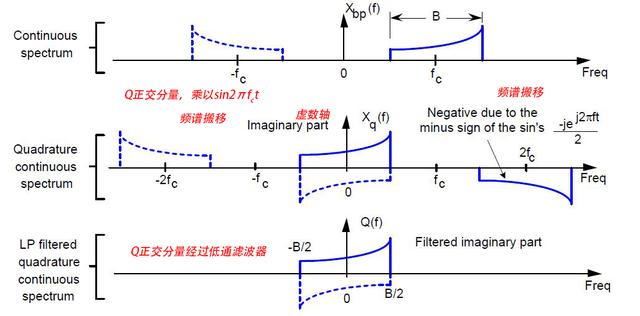
图12 正交分量

如果把同相与正交分量，放到三维坐标系内看，很明显，I同相分量只在实数轴平面，Q正交分量只在虚数轴平面，最后

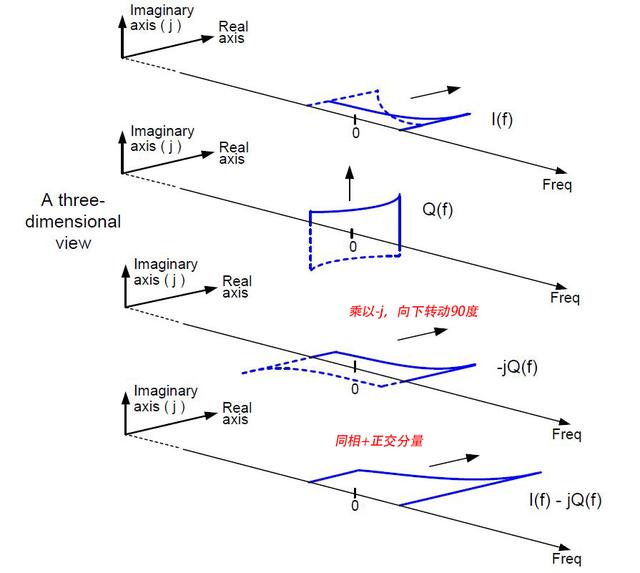
图13 三维分量

总结

调制本身就是要把传递的信号加载到载波上去，无非就是控制载波的振幅、相位、频率。这本来和复数没啥关系，但是当我们想同时传输两路信号之时，I和Q，这样的表达式，其实就是一个复数信号的实数部分。

我们也发现复数信号的频谱更加简单直观。所以在实际的信号处理中，我们为什么会”多此一举“的搞搞复数信号，这就是原因所在！

感谢参考文献：Richard Lyons.Quadrature Signals；

相关文章：单边带SSB信号：复数形式的解析信号，如何进行发送与接收？

模拟调制：我们为什么要调制？先从AM幅度调制开始

相干解调：三角函数公式有何用？原来就是通信中的调制解调过程

欢迎您点赞、关注@通信M班长，感谢！