random.sample设置生成数范围_【硬件算法笔记03】冗余数表示系统

72 阅读 0 评论 48 点赞

我是靠谱客的博主舒服手机，最近开发中收集的这篇文章主要介绍random.sample设置生成数范围_【硬件算法笔记03】冗余数表示系统，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

基于这本书：

https://zhuanlan.zhihu.com/p/258679655zhuanlan.zhihu.com

下文中，r表示基数，s表示数集。

进位问题

加法进位问题

加法器是许多运算器的基础器件，因此加法器的效率和开销就很重要。加法器也可能很慢或者电路开销很高，加法器的效率和开销主要和加法器的进位有关：

对于 k 位数的加法，简单的逐位进位（carry-ripple）加法器在最坏情况下将涉及 O(k) 次进位。
进位计算网络（carry computation network，即加法器中负责处理进位的那部分电路）是前瞻进位（carry-lookahead）等快速加法器设计中时间复杂度、面积开销等的核心来源

仅针对加法器的进位传播，这里有处理进位问题的几种办法：

减小可能的进位传播范围。
检测进位传播的结束，而不是简单的对每次运算都等一次最坏情况时间。
通过前瞻进位等技术加速进位传播。
理想情况：完全消除进位传播！

以一个例子讨论冗余表示与减少进位

首先不进位地计算两个十进制数的加法：

一个加法竖式，加数和被加数都是基10数集[0,9]上的数。这里不处理进位，分别将对应的每位相加，得到的结果是两数之和以基10的数集[0,18]的形式，在加法竖式横线下表示。

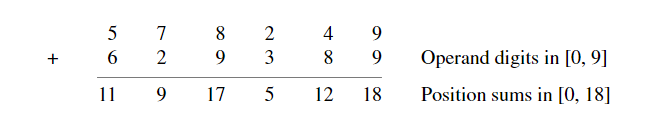
这样，使用r=10、s=[0,18]表示结果就避免了加法的进位。但这仅适用于第一次加法。（注意，r=10，s=[0,18]这样的表示系统就属于冗余表示）

以这种无进位方式将两个[0,18]上的数相加，将会产生一个在[0,36]上的结果，[0,36]可以被分解为 1个[0,2]上的数乘与10的结果和 1个[0,16]上的数的和，即：

而[0,2]和[0,16]两数集上的数可以无进位地和为[0,18]上的数：

也就是说可以这样将[0,36]转换为[0,16]，然后再将[0,16]转为[0,18]。

这是该过程的一个实例：

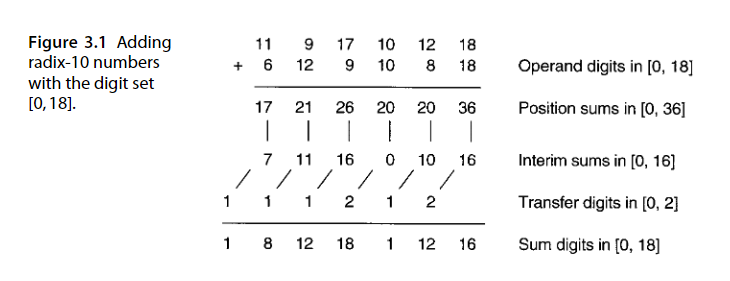
因此，即使不能做到真正的无进位传播加法，诺允许使用r=10，s=[0,18]表示数，让进位传播距离限制在1位传播范围内也是可行的：

两个[0,9]的数可以无进位地相加为一个[0,18]的数
两个[0,18]的数可以无进位地相加为一个[0,36]的数
[0,36]的数可以根据
转为[0,16]的数，而该过程中仅涉及一个距离为1的进位（

）。

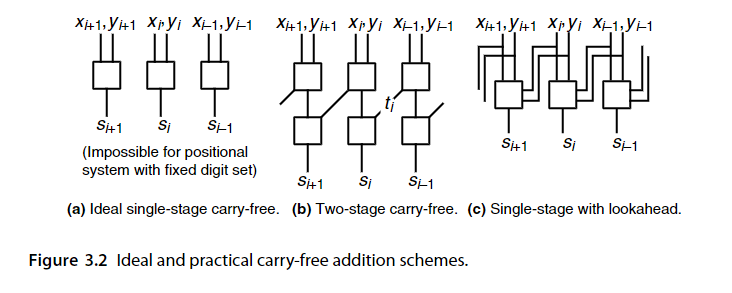
（理想中的）无进位（carry-free）加法器

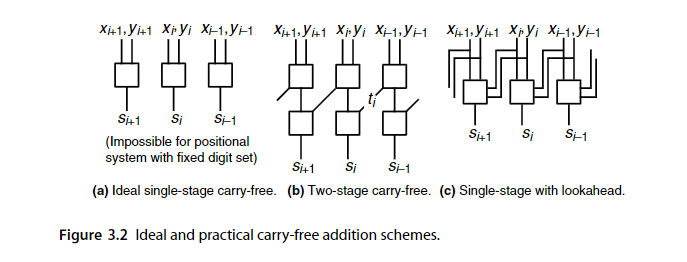
上图a是无进位加法器，在固定数集的定位表示系统中是不可能的。

我们之前讨论的，r=10，s=[0,18]的例子就对应着图b，进位最多传播一位。

图c是前瞻进位加法器，逐位进位加法器根据

来确定进位，而前瞻进位则根据

来更早地确定进位。

补充

图3.1避免进位的关键是r=10，s=[0,18].但实际上r=10，s=[0,11]就能实现一样的效果：

使用基10，数集[0,11]的数实现图3.1那样的无进位加法

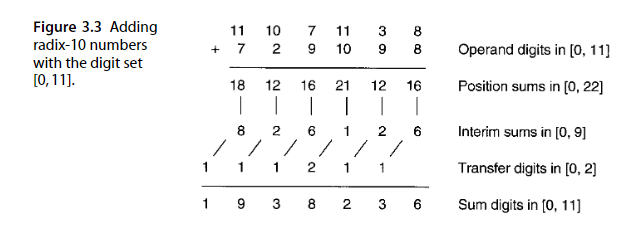
一个自然的问题是：需要多少冗余才能实现无进位加法？在本文的后面会讨论这个问题。

冗余算数

计算机算数中的冗余（redundancy）

冗余被广泛用于加速算数操作，最早的例子是1959年的[Metz59]，利用了r=2，s=[0,2]表示来快速地处理多个二进制数求和，下图是一个过程例子：

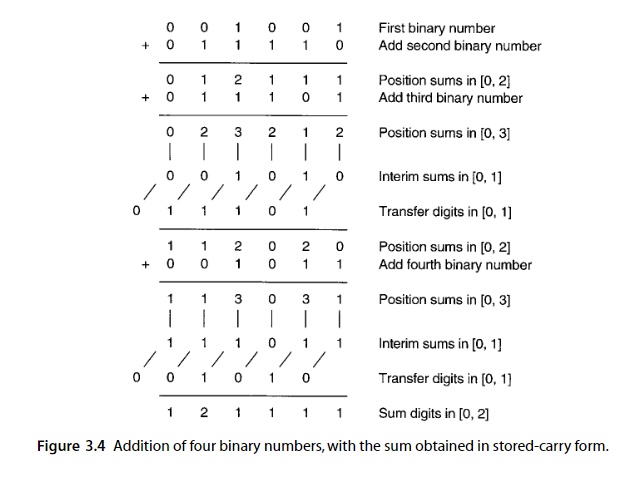
在硬件实现中，对应的运算单元是这样的：

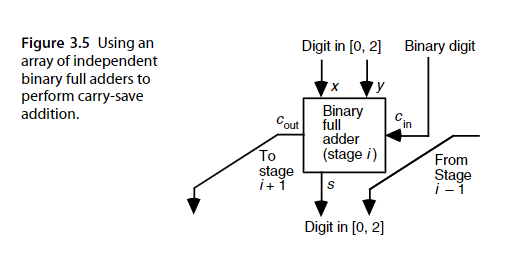
可以称它为进位保留加法器（carry save adder）或3:2计数器（3:2 counter）或3/2压缩器（3/2 reduction），因为相较于普通的加法器，它将进位竖出保留到了输出的[0,2]上，而不处理进位。

作为例子，基于进位保留加法器的求和运算器结构如下图：

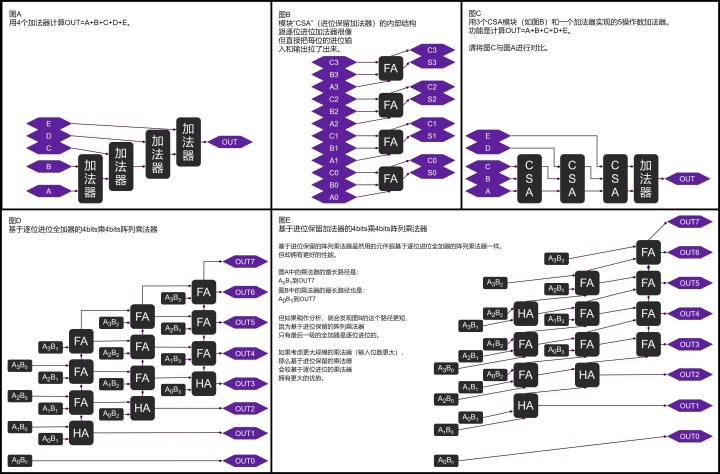
数集间的转换

常规的基r系统只使用标准的数集[0,r-1]。但除此外还有的许多其它的冗余或非冗余数字集。一个显然的结论是基r系统的数集必须至少包括r种不同的数码，如果数集所包含的不同数码数量大于r，就说这个数字系统是冗余的。

在冗余数表示中，不同数集间，如果输入数的当前位在输出的表示下容不下，就必须产生进位。比如r=10，s=[0,18]的“0 12 13”转换为r=10，s=[0,9]的表示就是“2 7 9“，第二位和第一位都向后面产生了进位。

下面是一些例子：

基10下，数集[0,18]表示转换到[0,9]表示

基2，[0,2]到[0,1]

数集包含负数的例子，基10，[0,18]到[-6,5]

基2，[0,2]到[-1,1]

广义有符号数

目前为止，我们已经知道，基r定位数系统的数集并不非得是[0,r-1]。

如果数集的形式是[-a,a]这样对称的，就说它是对称数集（symmetric digit sets）。

冗余和非冗余定位数系统的分类

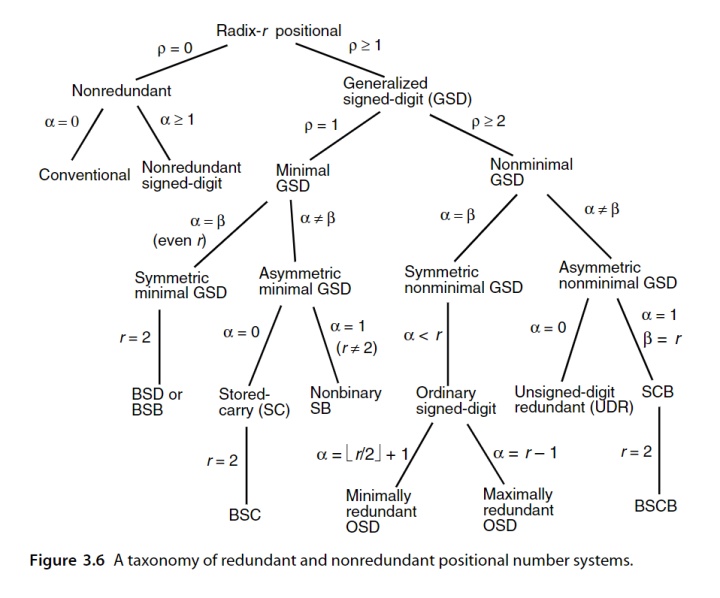
上图中，r表示基数，-α和β分别表示数集的上界和下界，也就是说上图是对基r，数集为[-α,β]的定位数表示系统的分类。一些术语的解释如下：

ρ：冗余指数（redundancy index），定义为ρ=α+β+1−r，即数集大小比基数大了多少
GSD：广义有符号数表示（generalized signed-digit (GSD) representation）
BSD或BSB：有符号二进制数（binary signed-digit）
OSD：普通有符号数表示（ordinary signed-digit (OSD) representation）
h：定义为h=α/(r−1)，是除ρ外量化冗余度的另一种方法，不适用于一般数集[-α,β]，高基除法就应用了h。h的另一个问题是它的值范围是1/2（对于无冗余）再到1（α=r-1）再到更大，冗余指数小于1是不寻常的，且可能产生误导。

一些例子

数集为[-1,1]的BSD的四种编码方式，实践中需要为BSD选择最合适的编码方式

用奇怪的符号表示BSD编码

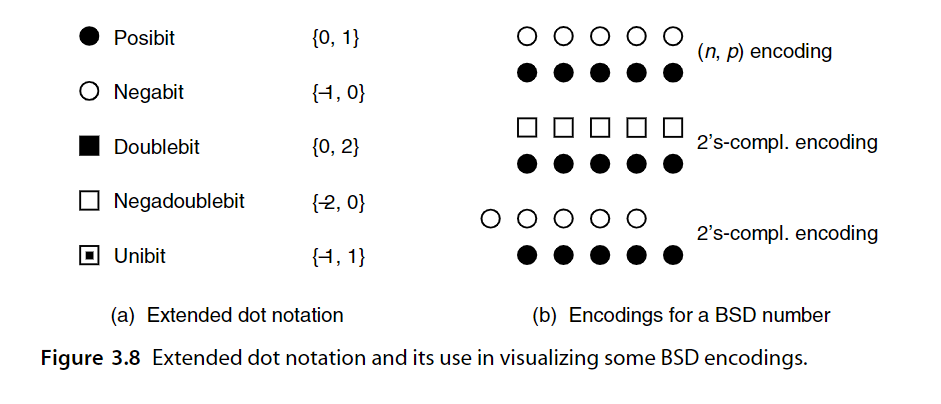
混合基数表示系统通过只在选定位置上引入冗余来达到算法速度和实现成本之间的平衡。

混合基数表示的加法的例子

用奇怪符号表示混合基数系统

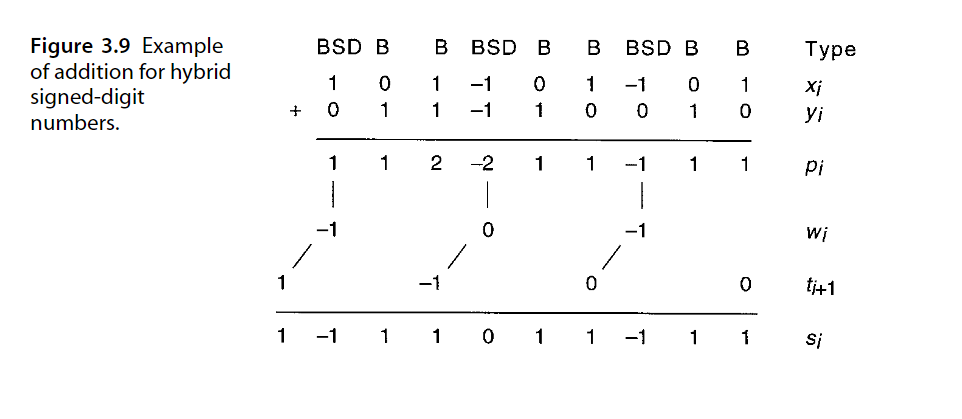
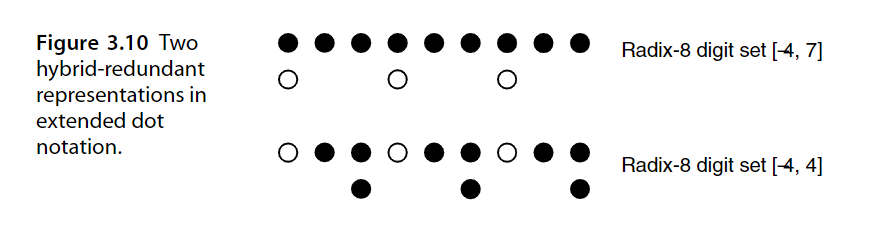
无进位加法算法

与Fig 3.2相对应的GSD无进位加法加法算法过程如下：

（GSD：广义有符号数表示，generalized signed-digit (GSD) representation）

其中

、

是加法器第 i 位输入，

就是它们的和。

是基数。

是第i+1位的进位输入（有限进位，在这个算法中

最多传播一位，即i到i+1），或者第i位的进位输出。

是第 i 位产生的进位输入或第i-1位的进位输出。

是

去除它要产生进位的部分

的结果。

是最终每位的输出。

其中

的值可以由

和一组所谓的比较常数

来计算，马上就会讨论。

下图展示该算法过程的一个具体例子：

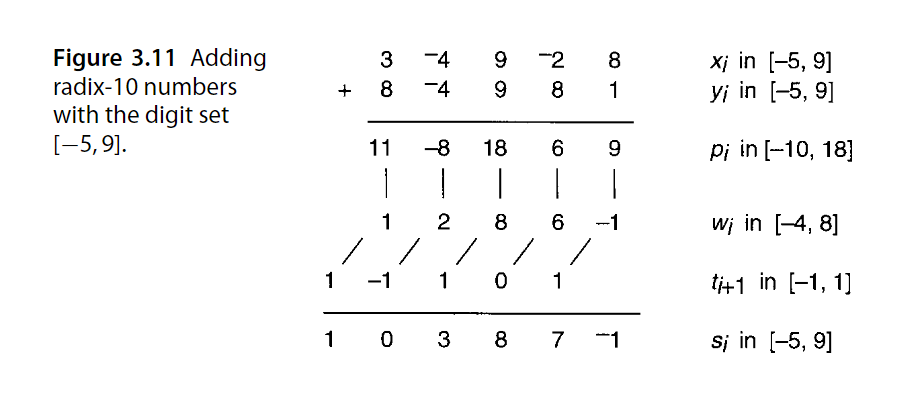
如果用[-λ,μ]表示

可能的取值范围，为确保最后一步

完成后不需要继续处理进位，即

在输入数的数集[-α,β]范围内，显然必须满足下条件：

从该不等式可以推导出等价条件：

。

如果我们确定了μ和λ的值，就可以通过比较

和

来确定所谓的比较常数

，其中

满足

。

可以用来确定进位

的取值：当且仅当

时有进位

。

[Parh90]中给出的公式能找到

的所有允许取值，下面的例子中给出了一个获得它的取值范围的一种简单直观的方法：

EXAMPLE 3.5

对于r=10和s=[-5,9]，为保证

，λ和μ应满足

。这里选择能最小化硬件复杂度的λ和μ：

即进位

的取值范围为[-1,1]。于是根据

、

和

可以得知：

接下来，我们演示一下

的合适取指范围的获得过程（原书就这么写，写的烂不怪我）：

由于

可知，可以令

的最小

为

：

对于

有

。刚好有

。诺

时使

，就有可能使得

了。（确定了

的最小值）

另一方面，对于

，显然必须令

，否则就是

，即

。（确定了

的最大值）

所以，能保证

的

应满足

。

的可取值范围就这么得到了。

在实现中，我们可以给每一个

设置一个符合这种取值范围的值，然后基于此，来确定

的取值。例如在这个例子中，我们可以设置：

，下图的例子就是在这个取值下计算的：

无进位算法的适用性

[Path]证明了，前文的无进位加法算法适用于冗余表示（redundant representation），当且仅当满足下面两个条件其中一个时：

有限进位加法算法

对于不满足上面两种条件的情况，如

、

或

。我们还可以使用所谓的GSD有限进位加法算法（Limited-carry addition algorithm for GSD numbers），其过程如下：

分别将每个
与一个常数比较，以确定每个

的值（

是对

的二值估计，非high即low）
基于
获得

，然后计算

GSD有限进位加法算法的图示如下Figure 3.12a。Figure 3.12b则是3.12a的一个替代方案，其中有关

的步骤被另一个进位

的生成和添加的步骤替代了。

虽然3.12a和3.12b看起来很类似，但从顶部和中间的方块的内部设计来看，它们的区别很大。

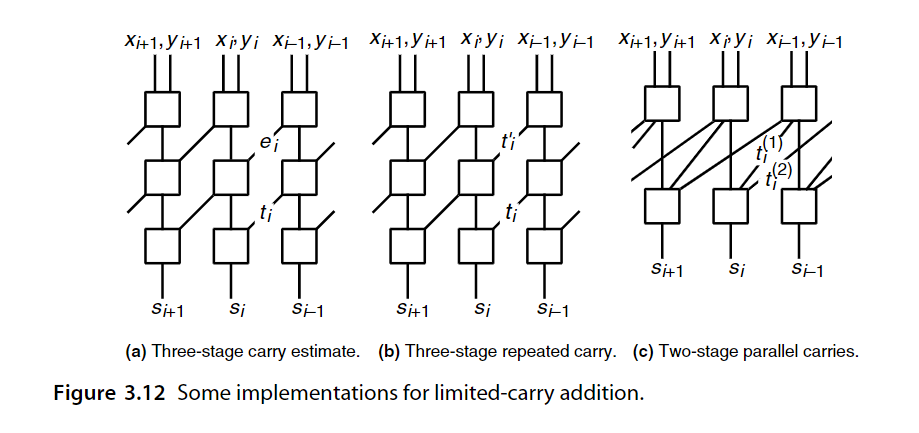
Fig3.12a和3.12b中，

的值都由

决定。所以，与其让第 i 位的进位逐位从 i 进到 i+1 再进到 i+2，不如直接一步到位，让第 i 位的进位直接进到 i+2 。Fig3.12c就是这样的设计，在第 i 位上直接并行生成了到 i+1 和 i+2 的进位信号。这个办法在不少情况下都是适用的。

一些例子

GSD的减法

GSD数字的减法和加法很像。对于带有对称数集（α=β）的，可以简单地通过翻转数的符号来通过加法实现减法（如，要计算 x+y ，可以先计算出 -y 的表示值，然后再计算 x+(-y) ）。

数集不对称的GSD数的取反（由y得到-y的表示值）要稍微麻烦一些。但仍可以基于[Parh93]的无进位算法实现。基本思路是将数集为[-β,α]的基r数转换回到原先的数集[-α,β]上。或者用另一种直接计算减法的方法：先在[-α-β,α+β]上计算差值，再处理一下进位（有限的）。

有关GSD的转换与功能支持

来自外界的输入通常由二进制或十进制表示（来自人或机器），输出也是同理。所以二、十进值与GSD间的转换是一个不可避免的问题。

EXAMPLE 3.10

考虑二进制与BSD间的转换。

以Fig3.7中s=[-1,1]的BSD与二进制间的转换为例：

如上图，过程就是先将该BSD的正负部分分开，然后将正负部分在二进制下相加。

冗余和非冗余表示间的转换在本质上在本质上涉及到了进位传播过程，因此相当缓慢。但所幸的是，数表示的转换通常仅在输入和输出的时候完成，而不在计算过程中涉及。也就是说，通常并不会涉及多少有关转换的运算。因此总体来看，开销一般可以忽略。

GSD与存储开销

存储开销（与相同表示范围的标准表示相比，GSD可能需要更多位数）曾是冗余表示的一个主要缺点，但随着VLSI（超大规模集成电路）的进步，这个问题不再显得那么重要，尽管增加了输入输出引脚的数量仍可能成为一个因素。

下面是对GSD表示一些基本特性的回顾，包括功能支持，0检测，符号测试，溢出处理等[Parh93]。

0检测

对于GSD数表示系统，整数0可能具有多种不同的表示方法。例如基4的三位数0 0 0和-1 4 0都可以表示0。

对于α<r和β<r的特殊情况，0仅唯一地由所有位为0的数（all-0s vector, 所有位都是0的数）表示。对于这种情况，判断数是否相等会比较简单，只会涉及减法和检测所有位是否为0。

符号测试

GSD的符号测试，还有关系比较（<,≤,=...）都比较困难。因为一般来说，一个GSD数的符号将取决于它的所有位的数，因此符号测试很麻烦（要涉及进位传播）。

对于α<r和β<r的特殊情况，其上的数x的符号，x最有效的那位（非零）数位的符号相同。但即使如此，确定符好也需要扫描所有位，这个过程可能跟进位传播的最坏情况一样慢。

溢出处理

GSD的溢出处理也很麻烦。考虑两个k位数的加法，其将产生一个最高进位输出

，可以知道

仅由未知的

在最坏情况下产生。

可以作为一个溢出的判断条件，但即使结果可以用 k 位数表示，也有可能会带有溢出指示

。可以执行一个测试来检查这个溢出是不是真的，如果不是，那就去尝试获得结果的真正 k 位数表示再判断，但这种测试和转换比较慢。

符好测试和溢出检测的困难会使得GSD数表示系统失去部分或全部的速度优势，所以目前GSD的应用仅限于特殊需求的特殊应用系统，或者用于内部的数字表示，但在输入和输出处对外转换为标准表示。

参考文献

[Aviz61] Avizienis, A., “Signed-Digit Number Representation for Fast Parallel Arithmetic,” IRE Trans. Electronic Computers, Vol. 10, pp. 389–400, 1961.

[Glas81] Glaser, A., History of Binary and Other Nondecimal Numeration, rev. ed., Tomash Publishers, 1981.

[Jabe05] Jaberipur, G., B. Parhami, and M. Ghodsi, “Weighted Two-Valued Digit-Set Encodings: Unifying Efficient Hardware Representation Schemes for Redundant Number Systems,” IEEE Trans. Circuits and Systems I, Vol. 52, No. 7, pp. 1348–1357, 2005.

[Jabe06] Jaberipur, G., B. Parhami, and M. Ghodsi, “An Efficient Universal Addition Scheme for All Hybrid-Redundant Representations with Weighted Bit-Set Encoding,” J. VLSI Signal Processing, Vol. 42, pp. 149–158, 2006.

[Korn94] Kornerup, P., “Digit-Set Conversions: Generalizations and Applications,” IEEE Trans. Computers, Vol. 43, No. 8, pp. 622–629, 1994.

[Metz59] Metze, G., and J. E. Robertson, “Elimination of Carry Propagation in Digital Computers,” Information Processing ’59 (Proceedings of a UNESCO Conference), 1960, pp. 389–396.

[Parh88] Parhami, B., “Carry-Free Addition of Recoded Binary Signed-Digit Numbers,” IEEE Trans. Computers, Vol. 37, No. 11, pp. 1470–1476, 1988.

[Parh90] Parhami, B., “Generalized Signed-Digit Number Systems: A Unifying Framework for Redundant Number Representations,” IEEE Trans. Computers, Vol. 39, No. 1, pp. 89–98, 1990.

[Parh93] Parhami, B., “On the Implementation of Arithmetic Support Functions for Generalized Signed-Digit Number Systems,” IEEE Trans. Computers, Vol. 42, No. 3, pp. 379–384, 1993.

[Parh96] Parhami, B., “Comments on ‘High-Speed Area-Efficient Multiplier Design Using Multiple-Valued Current Mode Circuits,’” IEEE Trans. Computers, Vol. 45, No. 5, pp. 637–638, 1996.

[Parh08] Parhami, B., “Double-Least-Significant-Bits 2’s-Complement Number Representation Scheme with Bitwise Complementation and Symmetric Range,” IET Circuits, Devices & Systems, Vol. 2, No. 2, pp. 179–186, 2008.

[Phat94] Phatak, D. S., and I. Koren, “Hybrid Signed-Digit Number Systems: A Unified Framework for Redundant Number Representations with Bounded Carry Propagation Chains,” IEEE Trans. Computers, Vol. 43, No. 8, pp. 880–891, 1994.

[Phat01] Phatak, D. S., T. Goff, and I. Koren, “Constant-Time Addition and Simultaneous Format Conversion Based on Redundant Binary Representations,” IEEE Trans. Computers, Vol. 50, No. 11, pp. 1267–1278, 2001.

[Tenc06] Tenca, A. F., S. Park, and L. A. Tawalbeh, “Carry-Save Representation Is Shift-Unsafe: The Problem and Its Solution,” IEEE Trans. Computers, Vol. 55, No. 5, pp. 630–635, 2006.