显然RNN是预测时间序列的,即前后文有关的一些预测,即在时间排列的基础上前后变量变化相关的预测。本文根据sin曲线规律预测cos曲线规律。
偷摸说一句,还有一篇博客写RNN(实际上是LSTM)识别手写照片,,,,不能理解,咋还能识别那个东西,一个手写数字照片,很明显每个照片28*28的像素点没有联系嘛真的是,,奇奇怪怪,非要乱来,置我CNN大法于何地。
呸
好进入正题。首先解释一下里面的一些东西。
首先这是一个预测时间序列的规律的题目。我们将batch设为50,即每50个坐标作为一组训练数据,这意味着这个RNN的cell也有50个。input_size和output_size都为1,因为分别对应横纵坐标嘛,一个数当然size为1。将cell_size设为10,意味着一个cell里面有10个隐藏节点,也就是有10个待求的值。这些就已经是所有的参数了。
可能有人不太理解为什么这些参数已经够了,说明对RNN的训练方式和过程不太理解,要去补一下MLP的训练方法和结构,以及RNN的结构,可在我其他的博客中找到。
其实还有一个参数,就是n_steps,此处设为3。不过对理解网络不重要,答案写在下面。
代码:
# import tensorflow.compat.v1 as tf
# tf.disable_v2_behavior()
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 首先说一下,对于tensorflow的后向传播误差算法(backpropagation),其以每一个batch为单位进行更新,在每一个batch时进行后向传播误差更新一次state,下一个batch就将本次batch更新得到的
# final state作为下次batch训练的initial state传进去,分段
# 普通的是一条线直接贯穿,即只有一个initial state,然后直接传入每次数据更新state
# 误差传播一般都是三步,即一个数据更新本cell和前面两个cell的参数
BATCH_STRAT=0
TIME_STEPS=20
BATCH_SIZE=50 # 每50个数据一批,即每次传入50个数
INPUT_SIZE=1 #因为预测的是点的坐标,所以一个点只有一个横纵坐标,故i_s和o_s都为1
OUTPUT_SIZE=1
CELL_SIZE=10
LR=0.006
BATCH_STRAT_TEST=0
# 生成数据函数,生成了最后的预测序列并且返回
def get_batch():
global BATCH_STRAT,TIME_STEPS # 要对外部变量进行赋值,首先要用global声明以下才能赋值成功
# xs shape (50 batch,20 steps)
# np.arange()函数返回一个有终点和起点的固定步长的排列,参数为2时,第一个参数为起点,第二个参数为终点,步长默认为1
xs=np.arange(BATCH_STRAT,BATCH_STRAT+TIME_STEPS*BATCH_SIZE).reshape((BATCH_SIZE,TIME_STEPS))/(np.pi)
seq=np.sin(xs) # 用sin序列来预测cos序列
res=np.cos(xs)
BATCH_STRAT+=TIME_STEPS
plt.plot(xs[0,:],res[0,:],'r',xs[0,:],'b--') # 红色实线是预测线,蓝色虚线是实际的seq,即回归预测问题,拿蓝色的虚线预测红色的实线
plt.show()
return [seq[:,:,np.newaxis],res[:,:,np.newaxis],xs]
class LSTMRNN(object):
def _init_(self,n_steps,input_size,output_size,cell_size,batch_size):
self.n_steps=n_steps # 此处为3,即每个cell的输出能够反向传播以更新参数的步数
self.input_size=input_size
self.output_size=output_size
self.cell_size=cell_size
self.batch_size=batch_size
# with方法,一种很方便和高效的控制语句,可自动打开和关闭要执行的语句,自动处理错误,as可有可无,
with tf.name_scope('inputs'):
# 申请空间,注意shape为三维,分别为数据个数,步数(即几步一更新参数,此处3步),输如输出长度(都为1)
self.xs=tf.placeholder(tf.float32,[None,n_steps,input_size],name='xs')
self.ys=tf.placeholder(tf.float32,[None,n_steps,output_size],name='ys')
with tf.variable_scope('in_hidden'): # 添加输入层
self.add_input_layer()
with tf.variable_scope('LSTM_cell'): # 添加cell层
self.add_cell()
with tf.variable_scope('out_hidden'): # 添加输出层
self.add_output_layer()
with tf.name_scope('cost'): # 计算cost
self.compute_cost()
with tf.name_scope('train'): # 开始训练
self.train_op=tf.train.AdamOptimizer(LR).minimize(self.cost)
# LSTMRNN有三层,输入层,cell层,输出层
# 输入层
def add_input_layer(self,):
# 为了计算,要把三维数据转换成二维,即[None,n_steps,input_size]==>[-1,self.input_size],其中二维的第一维大小batch*n_step,即50*3,第二维大小为1,即150行一列的矩阵作为输入参数
l_in_x=tf.reshape(self.xs,[-1,self.input_size],name='2_2D') # (batch*n_step,in_size)
# weight和bias都是调用下边的函数直接生成随机数作为初始数据,传入参数是shape,返回该shape的矩阵
# Ws(in_size,cell_size)
Ws_in=self._weight_variable([self.input_size,self.cell_size])
# bs(cell_size,)
bs_in=self._bias_variable([self.cell_size,])
# 计算第一层的输出值,即输出*权重+偏置
# 1_in_y=(batch*n_steps,cell_size)
with tf.name_scope('Wx_plus_b'):
l_in_y=tf.matmul(l_in_x,Ws_in)+bs_in
# reshape成3D: 1_in_y==>(batch,n_steps,cell_size)
self.l_in_y=tf.reshape(l_in_y,[-1,self.n_steps,self.cell_size],name='2_3D')
# cell层
def add_cell(self):
# 初始将forget_bias全开为1,意为不忘记,后续学习再慢慢忘记
lstm_cell=tf.nn.rnn_cell.BasicLSTMCell(self.cell_size,forget_bias=1.0,state_is_tuple=True)
with tf.name_scope('initial_state'):
# 每个cell都要有state,初始置为0,后续再变
self.cell_init_state=lstm_cell.zero_state(self.batch_size,dtype=tf.float32)
# rnn的循环操作,第一个参数是cell,即lstm_cell,第二个参数为输入,也就是上一层输入层的输出l_in_y,第三个参数为初始状态,第四个判断time_step是不是在主维度(不重要)
# 输出的是output和state,前者作为error进行矫正,后者作为本cell的final state传入下一步cell作为其initial state
# 注意,下面这句是一个循环,不断将得出的state传入作为初始state
# tf.nn.dynamic_rnn函数是实现RNN的封装函数
# 第一个参数cell:LSTM的记忆单元,即上面tf.nn.rnn_cell.BasicLSTMCell所创建的cell,其中上面的cell_size为cell中的神经元个数,作为参数传入
# 第二个参数inputs:输入的训练或者测试数据,一般格式为三维[batch_size, max_time, embed_size],分别为这批数据的数量,这批数据中序列的长度,嵌入的词向量的维度,对应于[batch_size,n_steps,cell_size]
# 第三个参数初始状态为0
# 第四个参数time_major:决定了输出tensor的格式,看n_steps是否位于第一维
# 函数返回值:元组(outputs,states)
# 返回值1很容易理解,每个cell都会有一个输出,作为比对label反向传递优化参数
# 返回值2表示最终的状态,也就是序列中最后一个cell输出的状态,因为cell为BasicLSTMCell,所以state形状为[2,batch_size, cell_size ],2对应LSTM中的cell state和hidden state
self.cell_outputs,self.cell_final_state=tf.nn.dynamic_rnn(
lstm_cell,self.l_in_y,initial_state=self.cell_init_state,time_major=False)
# 输出层
def add_output_layer(self):
# 上层得到的输出是三维的,即[batch,steps,cell_size],要将其转换成二维的,这样才能参与weight和bias的乘法运算
# shape=(batch*steps,cell_size)
l_out_x=tf.reshape(self.cell_outputs,[-1,self.cell_size],name='2_2D')
Ws_out=self._weight_variable([self.cell_size,self.output_size])
bs_out=self._bias_variable([self.output_size,])
# shape=(batch*steps,output_size)
with tf.name_scope('Wx_plus_b'):
self.pred=tf.matmul(l_out_x,Ws_out)+bs_out
# 计算cost,并且minimize(最小化)cost
def compute_cost(self):
losses=tf.nn.seq2seq.sequence_loss_by_example(
[tf.reshape(self.pred,[-1],name='reshape_pred')],
[tf.reshape(self.ys,[-1],name='reshape_target')],
[tf.ones([self.batch_size*self.n_steps],dtype=tf.float32)],
average_across_timesteps=True,
softmax_loss_function=self.msr_error, # 损失函数的一种,为tf.square(tf.sub(logits,labels)),即均方差函数
name='losses'
)
with tf.name_scope('average_cost'):
# tf.div(x,y):两个张量相除
self.cost=tf.div(# 相除得到平均cost
tf.reduce_sum(losses,name='losses_sum'),# 计算Loss的总和
# cast(x,dtype):张量数据类型转换,把张量x数据类型转换为dtype
tf.cast(self.batch_size,tf.float32),
# 用loss总和除以batch大小就是平均loss
name='average_cost')
# tf.summary.scalar(name,tensor):用来显示标量信息,第一个为生成节点的名字,第二个为包含一个值的实数tensor,一般求loss的时候会用到
# tf.summary.scalar('cost',self.cost) # 得到一个数,作为本函数的结果loss
# 把cost放入square进行计算,完了之后会在训练时进行minimize
def msr_error(self,y_pre,y_target):
return tf.square(tf.sub(y_pre,y_target)) # 损失函数,均方差函数
# 得到参数weight和bias
def _weight_variable(self,shape,name='weights'):
initializer=tf.random_normal_initializer(mean=0.,stddev=1.,)
return tf.get_variable(shape=shape,initializer=initializer,name=name)
def _bias_variable(self,shape,name='biases'):
initializer=tf.constant_initializer(0.1)
return tf.get_variable(name=name,shape=shape,initializer=initializer)
if __name__=='_main_':
# 建立model
model=LSTMRNN(TIME_STEPS,INPUT_SIZE,OUTPUT_SIZE,CELL_SIZE,BATCH_SIZE)
sess=tf.Session()
# merged=tf.merge_all_summaries()
# writer=tf.train.SummaryWriter("logs",sess.graph)
sess.run(tf.global_variables_initializer())
plt.ion() # 画动态图,打开交互模式,plt.ioff(),关闭交互模式
plt.show()
for i in range(200):
# getbatch拿到了seq和res,用seq预测res
seq,res,xs=get_batch()
if i==0:
feed_dict={
model.xs: seq,
model.ys: res,
# create initial state,刚开始不用初始状态,因为有
}
else:
feed_dict={
model.xs: seq,
model.ys: res,
model.cell_init_state: state # 此次运行用过去状态作为初始状态
}
_,cost,state,pred=sess.run(
[model.train_op,model.cost,model.cell_final_state,model.pred],
feed_dict=feed_dict)
# plotting,可视化学习过程
plt.plot(xs[0,:],res[0].flatten(),'r',xs[0,:],pred.flatten()[:TIME_STEPS],'b--')
plt.ylim((-1.2,1.2))
plt.draw()
plt.pause(0.3)
plt.show()
if i%20==0:
print('cost',round(cost,4))
# result=sess.run(merged,feed_dict)
# writer.add_summary(result,i)因为是初学,所以记录一下出现的每个函数。
代码中出现的函数解释
(1)np.arrange():函数返回一个有起点有终点的固定步长的序列,作为生成输入数据(横坐标)xs的函数。参数可以是1,2和3个。当是两个参数时,第一个参数为起点,第二个为终点,默认步长为1。
(2)tf.nn.rnn_cell.BasicLSTMCell(n_hidden, forget_bias=1.0, state_is_tuple=True):第一个参数n_hidden表示一个cell里神经元的个数;第二个参数forget_bias为LSTM门的忘记系数,等于1不会忘记任何信息,等于0全都忘记;第三个参数state_is_tuple默认为true,即返回的状态是用一个元组表示。这里面存在一个初始状态化函数,即zero_state(batch_size,dtype),batch_size即为输出样本每一批数据的大小。
(3)lstm_cell.zero_state(batch_size,dtype=tf.float32):即状态初始化函数:
(4)tf.nn.dynamic_rnn(cell, inputs, sequence_length=None,initial_state=None, dtype=None, parallel_iterations=None, swap_memory=False, time_major=False, scope=None):实现RNN的封装函数。
——第一个参数cell:LSTM的记忆单元,即上面tf.nn.rnn_cell.BasicLSTMCell所创建的cell,其中上面的cell_size为cell中的神经元个数,作为参数传入;
——第二个参数inputs:输入的训练或者测试数据,一般格式为三维[batch_size, max_time, embed_size],分别为这批数据的数量,这批数据中序列的长度,本例中为3,嵌入的词向量的维度,即cell_size,对应于[batch_size,n_steps,cell_size] ;
——第三个参数初始状态为0;
——第四个参数time_major:决定了输出tensor的格式,看n_steps是否位于第一维;
函数返回值:元组(outputs,states):
——返回值1很容易理解,每个cell都会有一个输出,作为比对label反向传递优化参数;
——返回值2表示最终的状态,也就是序列中最后一个cell输出的状态,因为cell为BasicLSTMCell,所以state形状为[2,batch_size, cell_size ],2对应LSTM中的cell state和hidden state。
(5)tf.nn.seq2seq.sequence_loss_by_example(logits,targets,weights):第一个参数logits是一个二维张量a*b,即本例中的预测值pred,shape为(batch*steps,output_size),第一维长度50*3;第二个参数targets是一个一维张量,且长度为logits的第一维长度a,本例中为真实值ys;第三个参数weights就是一个一维的张量,长度为a,是权重
(6)两种损失函数:
——tf.nn.sigmoid_cross_entropy_with_logits(labels=y,logits=logits):交叉熵函数,第一个参数为标准结果label,第二个参数为预测值;
—— tf.reduce_mean(tf.square(tf.sub(logits, labels))):均方差函数,参数意义同上。
——n_step设置为3的原因:
首先在普通或者tensorflow的RNN里,此参数都设置为3,意味着本cell的输出经过与label(即标准输出,也就是xt+1)比对后,得到的误差需要反向传播的步数,一直传播的前两个cell,只能更新到前两步的cell的参数。反向传播backpropagation自然不用说了,就是调节网络和更新参数的方法。
此处再写一下普通RNN和tensorflow中的RNN的不同之处:
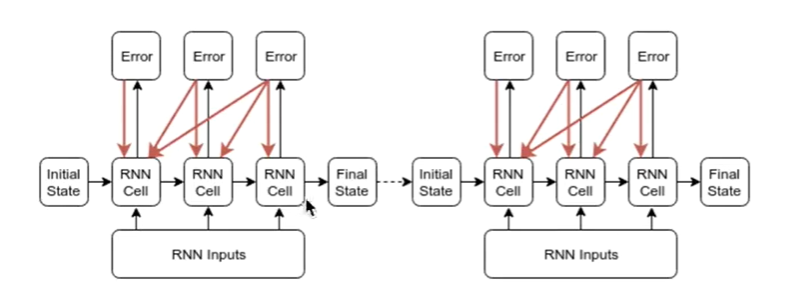
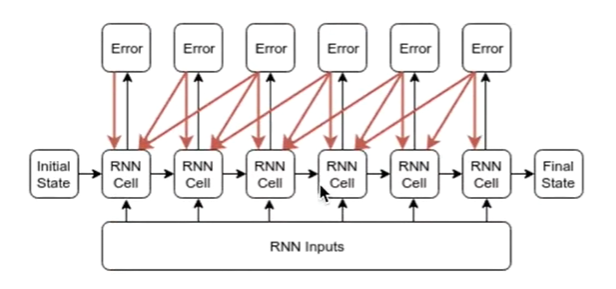
前者是tensorflow的RNN训练方法,其以每一个batch为单位进行更新,在每一个batch时进行后向传播误差更新一次state,下一个batch就将本次batch更新得到的final state作为下次batch训练的initial state传进去,
后者是普通的RNN,一条线直接贯穿,即只有一个initial state,然后直接传入每次batch数据更新state,只有一个初始state,每次batch的初始状态都一样的。
最后
以上就是背后麦片最近收集整理的关于【神经网络】学习笔记十—RNN实例1:时间序列sin曲线预测cos曲线的全部内容,更多相关【神经网络】学习笔记十—RNN实例1内容请搜索靠谱客的其他文章。








发表评论 取消回复