牛客小白月赛B-k-size字符串——逆元求组合数

62 阅读 0 评论 41 点赞

我是靠谱客的博主有魅力毛巾，最近开发中收集的这篇文章主要介绍牛客小白月赛B-k-size字符串——逆元求组合数，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

牛客小白月赛k-size字符串——逆元求组合数

题目链接：https://ac.nowcoder.com/acm/contest/5600/B
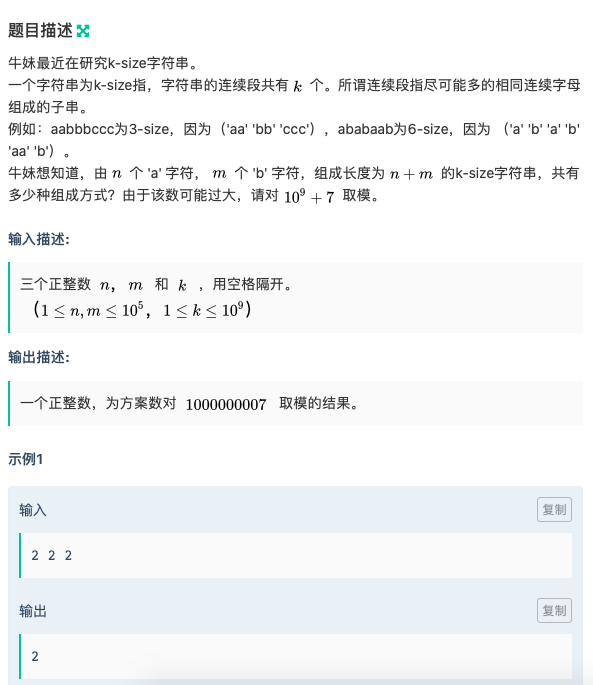
在这里插入图片描述

不要看它是以字符串的形式呈现，其实本质上是组合数学（自己细品），这就是我为什么不喜欢字符串的原因了，太能花哨了…

思路：因为连续段是和k有关的，所以k是要分奇偶的。首先先把最少的a和b根据k个排列好，在把剩下的a和b塞进去，可用高中知识的隔板法，可用大神拉马努金的整数拆分（这可是个神人啊！），关于整数拆分，可以看我上篇博客，这次就用排列组合就好了。

k为偶：那么最基本的形式就是abab…ab和baba…ba，这里用了k/2个的a和b，所以之前要判断一下，如果n-k/2或者m-k/2中有一个小于0，那答案不就是0了吗？好，如果都大于等于0的话，继续往下操作，a剩下n-k/2个，b剩下m-k/2个，这里就用简单的思路：

● △ ● △ ● △ ● △ ● △ ● △ ● △
(这里小圆圈代表a，小三角形代表b)

有k/2个a和k/2个b，所以只要把剩下的a和剩下的b插进去，如上图有k/2-1个插入位置，剩下的a有几种插法呢？我们给剩下的a+k/2，这样都让每个位置都能插一个，避免了有一个位置没有插进去的a，所以有C(n - 1, k / 2 - 1)中插法，请仔细思考一下。那么b的插法不也是和a一样的吗？所以当k为偶时，组合数=2*C(n-1, k / 2 - 1)*C(m - 1, k / 2 -1)。为什么要乘2呢？有没有忘记上面的abab和baba两种形式？

k为奇：根据上面的思路，最基本的形式就是abab…baba和baba…bab，这里就又要判断一下，用了多少个a和b，这里就交给你们自己推导一下了，最后的组合数为C(n-1, k / 2) * C(m - 1,k / 2 -1) + C(n - 1,k / 2 - 1)*C(m - 1, k / 2)。

最后这个组合数怎么求呢？因为分子分母太大可能会爆longlong，比如C(10000,5000)，那么该怎么求呢？有没有想起逆元的定义，如果想不起来了可以看我以前的博客乘法逆元。

因为组合也是分子/分母的形式，所以可以用逆元把除法转换成乘法，这样就可以用mod了。然后p是什么呢，1e9+7，这是一个素数啊，就可以知道用费马小定理求解逆元了，费马小定理可以用快速幂的方法。

思路大概就是这样，代码如下：

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef long double ld;

#define INF 0x7f7f7f
#define mem(a,b) memset(a , b , sizeof(a))
#define FOR(i, x, n) for(int i = x;i <= n; i++)
const ll mod = 1e9 + 7;
// const int maxn = 100005;

ll gcd(ll a, ll b)
{
    return b ? gcd(b, a % b) : a;
}

ll FPM(ll x,ll power)
{
    ll ans = 1;
    while(power)
    {
        if(power & 1)
        {
            ans = (ans % mod * x % mod) % mod;
        }
        x = (x % mod * x % mod) % mod;
        power >>= 1;
    }
    return ans % mod;
}

ll C(ll m, ll n)
{
    if(n * 2 > m)
        n = m - n;
    ll t = n;
    ll a = m, b = 1;
    ll ans = 1;
    while(t--)
    {
        ans = (ans % mod * (FPM(b, mod - 2) % mod * a % mod) % mod) % mod;
        a--;
        b++;
    }
    return ans % mod;
}

void solve()
{
    ll n, m, k;
    cin >> n >> m >> k;
    if(k == 1)
    {
        cout << "0";
        return ;
    }
    if(k % 2 == 0)
    {
        if((n - k / 2) < 0 || (m - k / 2) < 0)
        {
            cout << "0";
            return ;
        }
        cout << ((2 * C(n - 1, k / 2 - 1) % mod) % mod * C(m - 1, k / 2 - 1) % mod) % mod;
    }
    else
    {
        ll a = 0, b = 0;
        if((n - (k + 1) / 2) >= 0 && (m - k / 2) >= 0)
        {
            a = (C(n - 1, (k + 1) / 2 - 1) % mod * C(m - 1, k / 2 - 1) % mod) % mod;
        }
        if((n - k / 2) >= 0 && (m - (k + 1) / 2) >= 0)
        {
            b = (C(n - 1, k / 2 - 1) % mod * C(m - 1, (k + 1) / 2 - 1) % mod) % mod;
        }
        cout << (a % mod + b % mod) % mod;
    }
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
#ifdef FZT_ACM_LOCAL
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#else
    ios::sync_with_stdio(false);
    int T = 1;
    //cin >> T;
    while(T--)
        solve();
#endif
    return 0;
}