【ybtoj 高校进阶 6.2】 【质数与约数】 不定方程

题目

洛谷 P1445

解题思路

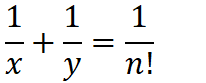
通分一下

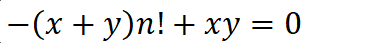
两边都加上（n!）²

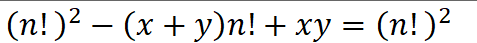
转换为

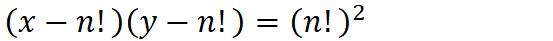
设a=(x-n!)，b=(y-n!)，ab=(n!)²
a是(n!)²的因数，且知道a一定能求出b
设n!=p1^c1+p2^c2+…+pk^ck
（n!）²=p1^2*c1+p2^2*c2+…+pk^2*ck
a的个数就有(2c1+1)(2c2+1)…(2*ck+1)
求c可以用公式

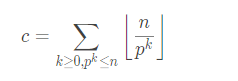
代码

#include<iostream>
#include<cstdio>
using namespace std;
const int mo=1e9+7;
int n,l,p[1000010];
long long c[1000010],ans=1,prm[1000010];
int main()
{
	scanf("%d",&n);
	for (int i=2;i<=n;i++)  //将质数筛出来
	{
		if (!p[i]) prm[++l]=i;
		for (int j=1;j<=l&&i*prm[j]<=n;j++)
		{
			p[i*prm[j]]=1;
			if (i%prm[j]==0) break;
		}
	}
	for (int i=1;i<=l;i++)  //求ci
	{
		int pi=prm[i];
		for (long long j=pi;j<=n;j*=pi) c[i]+=(n/j);
		c[i]=c[i]%mo;
	}
	for (int i=1;i<=l;i++)  //累计答案
	    ans=((2*c[i]+1)%mo*ans)%mo;
	printf("%lld",ans);
	return 0;
}

最后

以上就是安静书包最近收集整理的关于【ybtoj 高校进阶 6.2】 【质数与约数】 不定方程【ybtoj 高校进阶 6.2】 【质数与约数】 不定方程的全部内容，更多相关【ybtoj内容请搜索靠谱客的其他文章。