【Ybtoj 第28章例4】反素数【质数和约数】

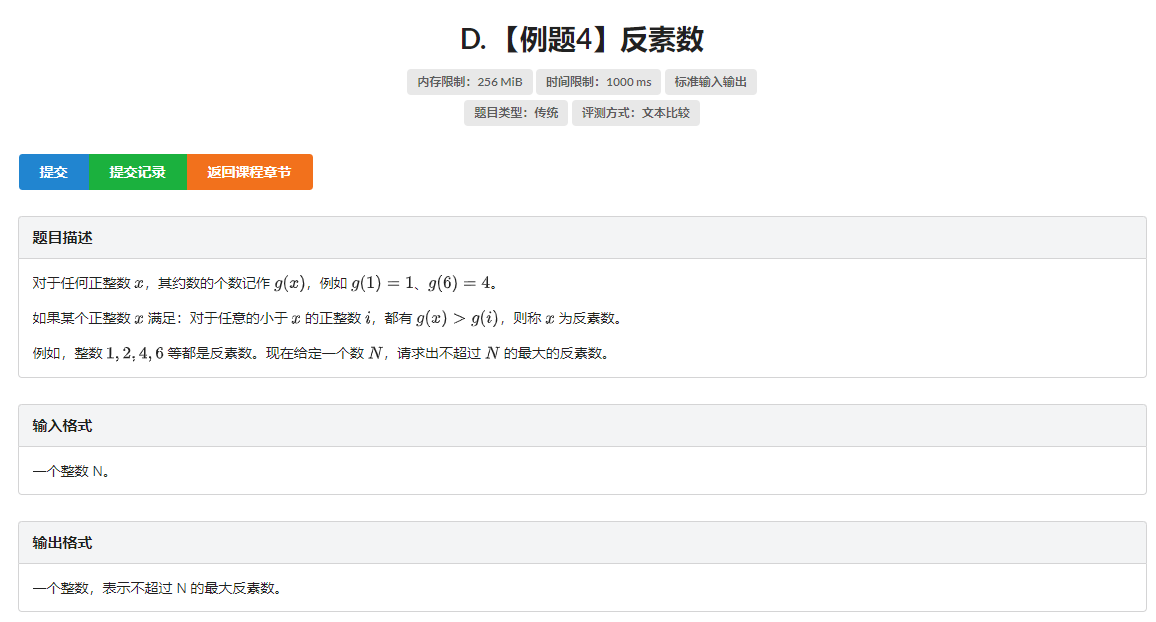
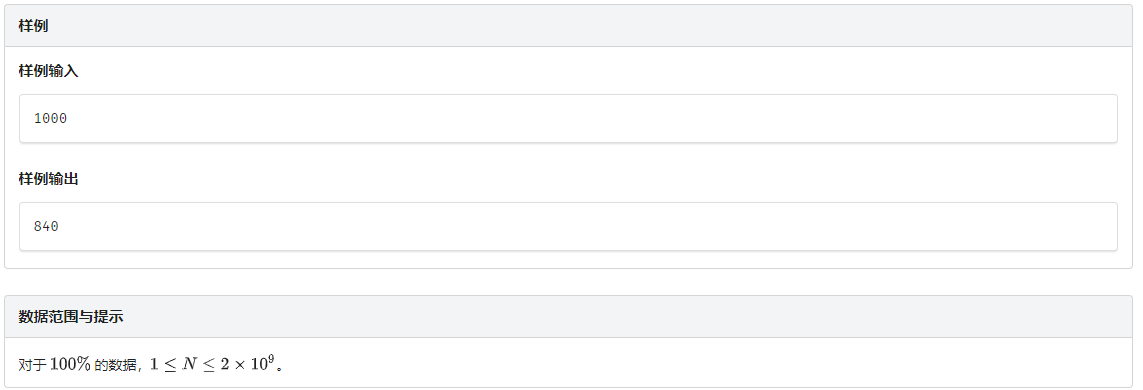
解题思路

首先1_{N中最大的反质数，就是1}N中约数个数最多的数中最小的一个。其次，如果不同的质因数因子超过10的话，就会超出$2\ast 10^9$，并且所有质因子的质数总和不会超过$30$，因为$2^{31}>2\ast 10^9$

并且我们要保证x的质因子是素数表中从2开始的连续若干个，且指数的质数单调递增。

证明：

1. 如果质数不是连续的话，也就是p_1p_3，那么我们还不如选择p_1p_2
2. 如果质数的指数不是单调递减的话，就会出现约数个数相等，但不是最小的情况。

根据上面的一系列性质，我们得出了最简洁的思路：使用DFS确定最小的十个质数的指数，且满足指数单调递减，总乘积不超过N，同时记录约数的个数。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<iomanip>
#include<cstring>
#include<cmath>
#include<map>
#include<queue>
#define ll long long
#define ldb long double
using namespace std;

ll n,maxn,lyx;
int pri[15]={0,2,3,5,7,11,13,17,19,23,29};

void dfs(int s,int x,ll sum,int dep){
	if(s>maxn||(s==maxn&&sum<lyx))
		maxn=s,lyx=sum;
	ll ans,k=sum,i=0;
	while(i<dep)
	{
		i++;
		k=pri[x]*k,ans=s*(i+1);
		if(k>n)
			return;
		dfs(ans,x+1,k,i);
	}
}

int main(){
	scanf("%lld",&n);
	dfs(1,1,1,30);
	printf("%lld",lyx);
}

最后

以上就是眯眯眼春天为你收集整理的【Ybtoj 第28章例4】反素数【质数和约数】的全部内容，希望文章能够帮你解决【Ybtoj 第28章例4】反素数【质数和约数】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。