数据结构 栈 逆波兰表达式

1.题目

逆波兰表达式又叫做后缀表达式。在通常的表达式中，二元运算符总是置于与之相关的两个运算对象之间，所以，这种表示法也称为中缀表示。

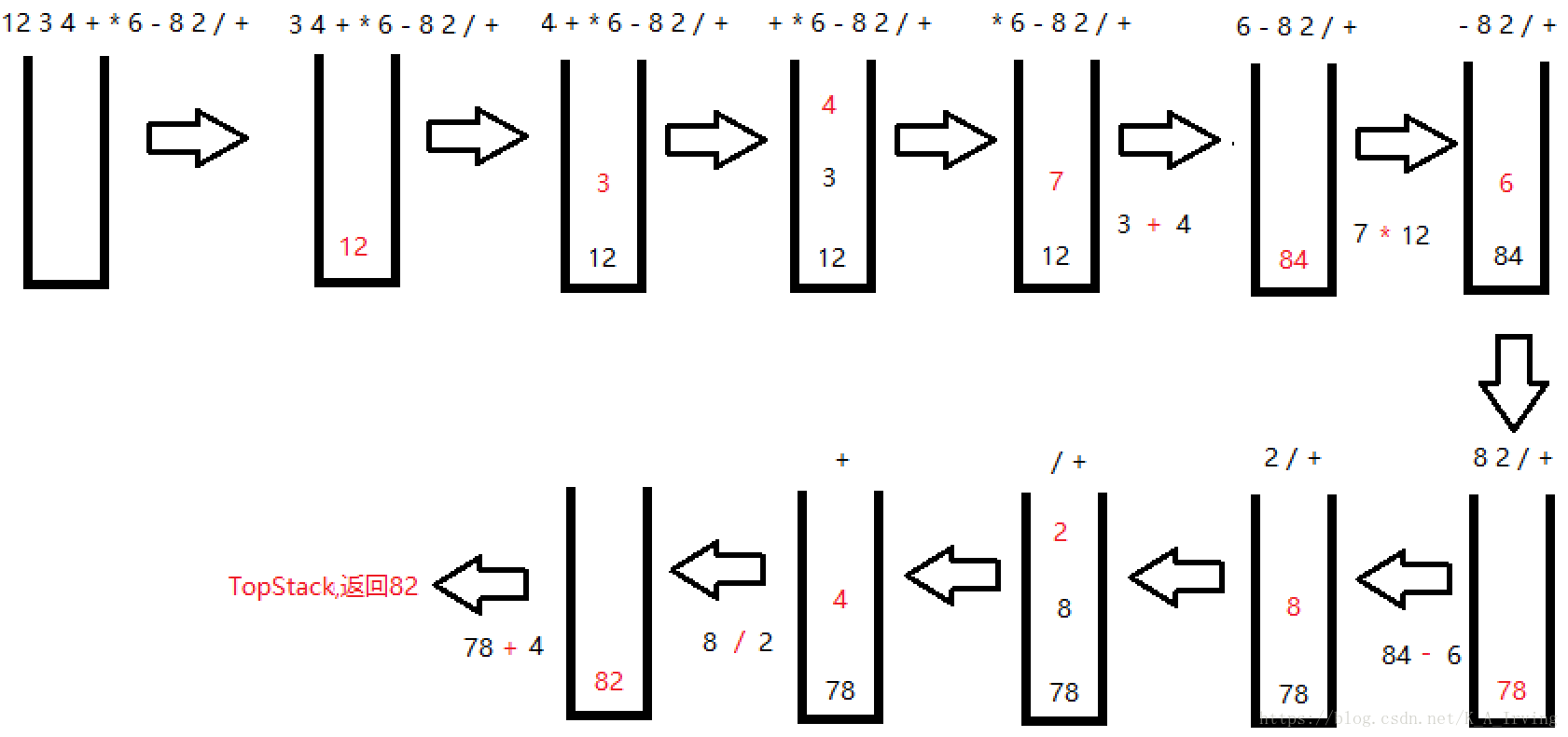
12*(3+4)-6+8/2 的逆波兰表达式为12 3 4 + * 6 - 8 2 / +
用栈计算该逆波兰表达式的值

2.基本思路

把逆波兰表达式以结构体数组的方式存储，结构体包含两个元素，第一个元素是说明这个符号是数据还是运算符号，第二个符号是数据，若该符号为运算符，则可以给任意值，不影响结果，然后用一个结构体指针依次取出该数组中的元素，当为数字时，把结构体中的数字压入栈中，若为运算符，则取出栈中前两个数据，分别作为右操作数和左操作数（因为栈中后进去的元素现出来，所以先取出的是右操作数），然后与运算符进行相应的运算，把运算结果压入栈中

3.程序代码

//RPN.h
#ifndef __RPN_H__
#define __RPN_H__

#include <stdio.h>
#include <Windows.h>
#include <assert.h>

#define MAXSIZE 10
typedef int DataType;

//定义栈
typedef struct StackNode
{
    DataType arr[MAXSIZE];
    int top;
}Stack, *pStack;

//枚举，
enum { ADD, SUB, MUL, DIV, DATA };

//定义一个结构体，分别存放符号和数据
typedef struct RPN
{
    int opera;
    int data;
}RPN;

int EmptyStack(pStack ps);
void InitStack(pStack ps);
void PushStack(pStack ps, DataType data);
void PopStack(pStack ps);
DataType TopStack(pStack ps);

#endif // !__RPN_H__

//RPN.c
//对栈初始化
void InitStack(pStack ps)
{
    assert(ps);

    ps->top = 0;
}
//入栈
void PushStack(pStack ps, DataType data)
{
    assert(ps);

    ps->arr[ps->top++] = data;
}
//判断栈中是否为空
int EmptyStack(pStack ps)
{
    assert(ps);

    return 0 == ps->top;
}
//出栈
void PopStack(pStack ps)
{
    assert(ps);

    if (EmptyStack(ps))
    {
        return;
    }

    ps->top--;
}
//求栈顶的元素
DataType TopStack(pStack ps)
{
    assert(ps);
    if (EmptyStack(ps))
    {
        printf("栈为空!!!n");
        return;
    }
    return ps->arr[ps->top - 1];
}

//test.c
#include "RPN.h"

int _RPN(RPN* p, int size)
{
    int left, right;
    Stack s;//创建一个栈
    InitStack(&s);

    while (size--)
    { 
        if (DATA == p->opera)//当结构体数组中的第一个为DATA时，说明该位置存放的是数据，需要入栈
        {
            PushStack(&s, p->data);
        }
        else
        {
        //为其他时，则说明遇到了算数符号，将栈中的两个元素出栈，分别作为右操作数和左操作数
            right = TopStack(&s);
            PopStack(&s);
            left = TopStack(&s);
            PopStack(&s);

            switch (p->opera)
            {//当符号为加减乘除时分别进行相应的操作
            case ADD:
                PushStack(&s, left + right);
                break;
            case SUB:
                PushStack(&s, left - right);
                break;
            case MUL:
                PushStack(&s, left * right);
                break;
            case DIV:
                PushStack(&s, left / right);
                break;
            }
        }
        p++;//将指针向后移动，获取下一个结构体的内容
    }

    return TopStack(&s);
}

int main()
{
    //创建一个数组存放逆波兰表达式
    RPN p[] = { {DATA, 12}, {DATA, 3}, {DATA, 4},
    {ADD, 0}, {MUL, 0}, {DATA, 6}, {SUB, 0},
    {DATA, 8}, {DATA, 2}, {DIV, 0}, {ADD, 0} };

    int size = sizeof(p) / sizeof(p[0]);
    int result = _RPN(p, size);
}

4.执行结果

最后

以上就是沉默冬瓜为你收集整理的数据结构 栈 逆波兰表达式的全部内容，希望文章能够帮你解决数据结构 栈 逆波兰表达式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。