文章目录
- 三、标记—整理回收
- 3.1 双指针整理算法(任意顺序)
- 原理
- 步骤
- 3.2 Lisp 2算法(滑动顺序)
- 原理
- 步骤
- 3.3 引线整理算法(滑动顺序)
- 原理
- 步骤
- 3.4 单次遍历算法(滑动顺序)
- 原理
- 步骤
- 四、复制式回收
- 4.1 半区复制回收
- 原理
- 4.1.1 工作列表的实现
- Cheney扫描(Cheney scanning)算法
- 4.2 遍历顺序与局部性
- 启发式方法
- 优化深度优先
- 为什么广度优先不行
- 在线对象记录
- 其他方式
- 附录
三、标记—整理回收
内存碎片化是非移动式回收器无法解决的问题之一,即:尽管堆中仍有可用空间,但是内存管理器却无法找到一块连续内存块来满足较大对象的分配需求,或者需要花费较长时间才能找到合适的空闲内存。
许多长期运行的程序,如果通过非移动式回收器进行内存管理,通常会出现碎片化问题,进而导致程序性能的下降。
标记—整理通过标记后,将所有存活对象重新整理,让它们紧紧挨着,以减少碎片化。(和我们硬盘的碎片化整理一样)
标记—整理算法的执行需要经过数个阶段:
- 首先是标记阶段,其相关内容我们在上一章已经讨论过
- 然后是整理阶段,即移动存活对象,同时更新存活对象中所有指向被移动对象的指针。
在不同算法中,堆的遍历次数、整理过程所遵循的顺序、对象的迁移方式都有所不同。
整理顺序( compaction order)会影响到程序的局部性。移动式回收器重排堆中对象时所遵循的顺序包括以下3种:
-
任意顺序:对象的移动方式与它们的原始排列顺序和引用关系无关。
-
线性顺序:将具有关联关系的对象排列在一起,如具有引用关系的对象,或者同一数据结构中的相邻对象。
-
滑动顺序:将对象滑动到堆的一端,“挤出”垃圾,从而保持对象在堆中原有的分配顺序。
我们所了解的整理式回收器大多遵循任意顺序或者滑动顺序。任意顺序整理实现简单,且执行速度快,特别是对于所有对象均大小相等的情况。但任意顺序整理很可能会将原本相邻的对象分散到不同的高速缓存行或者虚拟内存页中,从而降低赋值器空间局部性。
所有现代标记——整理回收器均使用滑动整理顺序,它不改变对象的相对排列顺序,因此不会影响赋值器局部性。
复制式回收器甚至可以通过改变对象排布顺序的方式将对象与其父节点或者兄弟节点排列得更近,从而提升赋值器的局部性。一些实验表明,由任意顺序整理导致的对象重排列会大幅降低应用程序的吞吐量。
整理算法可能会存在多种限制:
- 任意顺序算法只能处理单一大小的对象,或者只能对不同大小的对象分别进行整理;
- 整理过程需要两次甚至三次整堆遍历
一遍标记并将存活对象连起来比如用指针,一遍更新引用,一遍移动对象到新的区域。
需要注意的是,我们标记用的是类似根可达的方式,因此标记顺序和内存地址的顺序可能是不一样的
- 对象头部可能需要一个额外的槽来保存迁移信息,这对于通用内存管理器来说是一个显著的额外开销。
整理算法可能对指针有特定限制,如指针的引用方向是什么?是否允许使用内部指针?
所有整理式回收算法的执行都遵从如下范式:

3.1 双指针整理算法(任意顺序)
Edwards 的双指针算法属于任意顺序整理算法,其需要两次堆遍历过程,最佳适用场景为只包含固定大小对象的区域。
原理
对于某一区域中的待整理存活对象,回收器可以事先计算出该区域整理完成后存活对象的 “高水位标记”( high-water mark),地址大于该阈值的存活对象都将被移动到该阈值以下。
步骤
- 第一次遍历
- 指针free指向区域始端,指针scan 指向区域末端。
- 在第一次遍历过程中,回收器不断向前移动指针free,直到在堆中发现空隙(即未标记对象)为止
- 类似地,不断向后移动指针scan直到发现存活对象为止。
- 如果指针free和指针scan发生交错,则该阶段结束,否则便将指针scan所指向的对象移动到指针free的位置,同时将原有对象中的某个域(指针scan 所指向的)修改为转发地址,然后继续进行处理。
图3.1 描述了这一过程,其中对象A被移动到新的位置A’,且在对象A中的某个槽(即第一个槽)中记录了A’的地址。
值得注意的是,该算法的整理质量取决于指针free所指向的空隙与指针scan 所指向的存活对象大小的匹配程度。除非对象大小固定,否则碎片的整理程度一定很低。
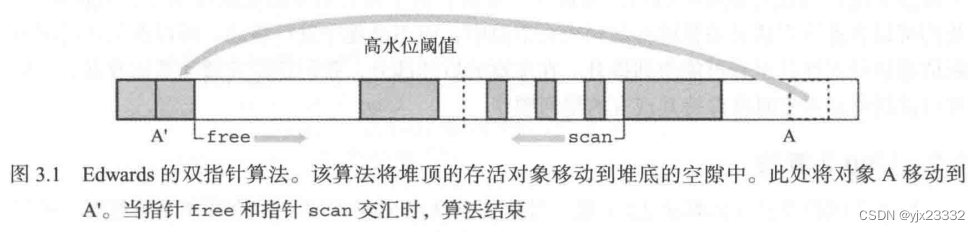
该阶段完成后,指针free将位于存活对象边界。
- 第二次遍历
回收器在该过程中会将指向存活对象边界之外的指针更新为其目标对象中所记录的转发地址,即对象的新位置。


优势:
- 简单快速,且每次遍历过程的操作较少。
- 该算法支持内部指针。其内存访问模式是可预测的,因此也支持预取(不论是硬件预取还是软件预取),进而可以提升回收器的高速缓存友好性。
缺点
- 需要将标记位保存在一个独立的位图中,或者在对象分配时即在位图中记录其首地址
- 双指针算法重排列堆中对象的顺序是任意式的,因此会破坏赋值器的局部性。
但是,由于相关对象总是成簇诞生、成批死亡,我们可以将连续存活对象整体移动到较大空隙中,而不是逐个进行移动,所以在某些情况下赋值器的局部性甚至有可能得到提升。
3.2 Lisp 2算法(滑动顺序)
Lisp 2回收算法(见算法3.2)是一种历史悠久的回收算法,无论是其原始形态,还是为适应并行回收的改进版本,都得到了广泛应用。
原理
它需要在每个对象头部额外增加一个完整的头域来记录转发地址(标记位也可以复用该域)
在标记阶段结束之后的第一次堆遍历过程中,回收器将会计算出每个存活对象的最终地址(即转发地址),并且将其保存在对象的forwardingaddress域中(见算法3.2)。
步骤
用computeLocations方法在堆中移动两个指针:
- 指针scan对来源区域中的所有(存活的或死亡的)对象进行迭代
- 指针free指向目标区域中的下一个空闲位置。
computeLocations方法需要3个参数:
-
堆中待整理区域的起始地址
-
堆中待整理区域的结束地址
-
整理目标区域起始地址。
- 第一次遍历
目标区域通常与待整理区域相同,但并行回收器可能会为每个线程设定不同的来源和目标区域。
-
如果指针scan遍历到的对象是存活的,意味着该对象(最终)会被移动到指针free所指向的位置。此时回收器将指针free写入对象的forwardingaddress域,然后根据对象的大小向前移动指针free(需要考虑对齐填充)。
-
如果遍历到死亡对象,则将其忽略。
- 第二次遍历
在第二次堆遍历过程(算法3.2中的updateReferences方法)中,回收器将使用对象头域中记录的转发地址来更新赋值器线程根以及被标记对象中的引用,该操作将确保它们指向对象的新位置。
- 第三次遍历
在第三次遍历过程中, relocate最终将每个存活对象移动到其新的目标位置。
需要注意的是,遍历的方向(从低地址到高地址)与对象的移动方向(从高地址到低址)相反,这便可以保证回收器在第三次遍历过程中复制对象时其目的地址已经腾空。


某并行回收器将堆划分为多个内存块,并且在相邻内存块上使用不同的滑动方向,相对于每内存块都向同一个方向滑动的算法,该算法可以产生较大的对象“聚集”,进而产生更大的空闲内存间隙,图14.8即是一个示例。
Lisp 2算法可以在多方面进行改进:
-
标记—清扫回收器在清扫阶段的数据预取技术也可以应用在Lisp 2算法中
-
在computeLocations方法的第10行之后,回收器可以将相邻垃圾合并,以提升后续遍历过程的性能。
Lisp 2算法的主要缺陷有两个:
-
算法需要三次完整的堆遍历过程
-
每个对象需要额外的空间来记录转发地址,这两个缺陷可以说是互为因果
3.3 引线整理算法(滑动顺序)
原理
Fisher通过一种不同的策略解决了指针更新问题,即 “引线”( threading) ,该算法不需要任何额外存储,且支持滑动整理。
引线算法要求对象头部存在足够的空间来保存一个地址(如果必要可以覆盖头域的其他数据),这一要求并不苛刻,但回收器所记录的地址必须要能与其他值区分,要满足这一要求可能有些困难。最知名的引线算法当属Morris的版本,但是Jonkers的版本限制更少(例如在指针方向上)。
引线的目的是通过对象N可以找到所有引用了该对象的对象,实现方法是临时反转指针的方向。
步骤
图3.2演示了如何在引线之后找到之前引用了对象N的对象。需要注意的是,经过图3.2b 中的引线操作之后,对象N头部info域的值被写入到对象A的一个指针域中,当回收器通过指针追踪来逆引线(unthread)、更新引用时,必须要能分辨出对象A的这一域中记录的并非引线指针。
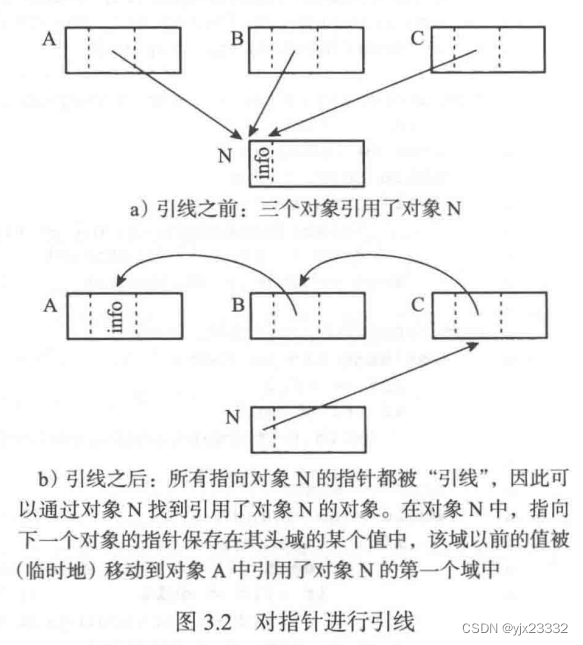
Jonkers的算法需要两次堆遍历过程,第一次遍历实现堆中前向指针的引线,第二次遍历实现堆中后向指针9的引线(见算法3.3)。
在第一次遍历开始时,回收器先对根进行引线,然后在堆中从头到尾进行扫描,与此同时,将所有存活对象的大小累加,最终以此来更新指针free。
在图3.2中,如果仅考虑存活对象N,那么该算法很容易理解:
- 当回收器在第一次遍历过程中遇到对象A时,其会对A中指向对象N的引用进行引线
- 当遍历到对象N时,会完成所有指向对象N的前向指针的引线(见图3.2b)
- 此时回收器可以沿着对象N的这条引线链完成所有指向对象N的前向指针的更新,即将它们都改写为指针free,也就是对象N未来的新地址
- 当到达引线链的终点时,回收器将恢复对象N头部info域的值
- 完成上述步骤之后,还需要增加指针free,并对N的所有子节点进行引线
第一次遍历完成之后,所有前向指针都已经指向了对象整理后的新地址,且所有后向指针都已完成引线。
第二次遍历过程则会根据后向指针引线链简单地更新指向对象N的引用,同时完成对象N的移动。

优点:
- 需要额外的空间,尽管其对象头部必须能够容纳一个指针(且该指针必须能与一般的值进行区分)。
缺点:
-
该算法需要两次修改对象的头部,第一次是引线,第二次是逆引线并更新引用。
-
与标记过程类似,Jonkers的算法中沿着引线链进行遍历的高速缓存友好性较差,而整个算法总共需要三次这样的指针遍历过程(即:标记、引线、逆引线)。
Martin指出,可以将标记过程与第一次整理过程合并,从而将回收时间减少三分之一,但这也反映了指针追踪以及修改指针域的开销之大。
Jonkers的算法对指针的修改是破坏性的,其本质上是串行的,因此无法用于并发整理。
例如在图3.2b中,当回收器完成对象B中第一个指针域的引线之后,堆中将不再有任何能够反映出该域曾经指向对象N这一信息(除非将对象N的地址存储在指针链的末端,即在对象A的头部中占用一个额外的槽,但这破坏了不使用额外空间的本意)。
最后,Jonkers 的算法不支持内部指针(interior pointer),这在某些场景下可能是一个重要问题。Morris的引线整理算法虽然支持内部指针,但其代价是要求为每个域分配一个额外的标签位,且第二次整理过程的遍历方向必须与第一次相反(从而引入了堆的可解析性问题)。
3.4 单次遍历算法(滑动顺序)
如果要将滑动式回收器的堆遍历次数降低到两次(一次标记、一次滑动对象),且避免昂贵的引线开销,那么就必须使用一个额外的表来记录转发地址。
所谓的单次应该指的是标记之后只循环一次
Abuaiadh等,Kermany和 Petrank各自独立设计出了可以完全满足这一要求且适用于多处理器的高性能整理算法:
-
前者的算法属于并行式、万物静止式算法(使用多个整理线程);
-
后者的算法可以配置成并发式回收算法(允许赋值器线程和回收器线程同时执行)和增量式回收算法(定期挂起一个赋值器线程并简单地执行小部分回收工作)。
这两种算法都需要使用数个额外的表或者向量。
原理
与许多回收器类似,标记过程是基于位图(即图3.3中的标记向量——译者注)进行的,每个位对应堆中一个内存颗粒(即一个字)。
在标记过程中,如果发现存活对象,则设置其所占用空间的第一个和最后一个内存颗粒对应的位。
例如在图3.3中,回收器会针对存活对象old设置标记向量的第16位和第19位。回收器在后续的整理阶段可以通过对标记向量的分析计算出任意存活对象的大小。
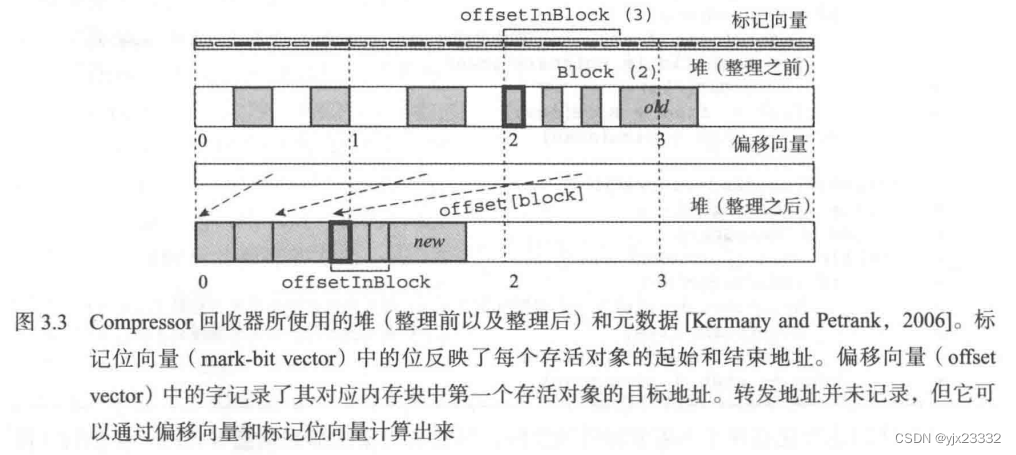
回收器使用一个额外的表来记录转发地址。如果记录每个对象的转发地址,则会引入难以承受的开销(即使对象已经满足一定的字节对齐要求),因此这两种算法都将堆划分成大小相等的小内存块(分别是256字节和512字节)。
偏移向量(offset vector) 记录了每个内存块中第一个存活对象的转发地址,其他存活对象的转发地址可以通过偏移向量和标记位向量实时计算得出。
对于任意给定对象,我们可以先计算出其所在内存块的索引号,然后再根据该内存块在偏移向量和标记位向量中的对应数据计算出该对象的转发地址。
因此回收器不再需要两次遍历过程来移动对象和更新指针,转而可以通过对标记位向量的一次遍历来构造偏移向量,然后通过一次堆遍历过程同时完成对象的移动和指针的更新。减少堆的遍历次数可以提升回收器的局部性。
步骤
下面我们将分析算法3.4(即 Compressor算法)的具体实现细节。

在标记过程结束之后,computeLocations方法将通过对标记位向量的遍历来计算偏移向量。从本质上讲,这一过程与Lisp 2(见算法3.2)中的计算方法一致,但它不需要访问堆中对象。
我们以图3.3中 block 2内的第一个存活对象为例(即图中加粗的方块),block 0中的第2、3、6、7位被设置, block 1中的第3、5位被设置(本例中,每个内存块包含8个槽),这表示在该对象之前已经有7个内存颗粒(字)在位图中得到了标记,因此block 2中的第一个存活对象将被移动到堆中第7个槽中。回收器将这一地址记录在与该块对应的偏移向量中(图中标有offset [block]的虚线)。
完成偏移向量的计算后,回收器将更新根以及存活域,并使其指向对象的新地址。
在Lisp 2算法中,由于迁移信息记录在堆中,且堆中对象的移动会破坏原有对象的迁移信息,因此回收器需要将更新引用和移动对象的过程分开。
但在Compressor算法中,转发地址可以快速地通过标记位向量和偏移向量实时计算得到,因而无须将其保存在堆中,于是回收器可以在单次遍历过程中同时完成对象的迁移以及引用的更新,即算法3.4中的updateReferencesRelocate方法。对于堆中任意给定地址的对象,Compressor回收器均可通过newAddress方法获取其内存块编号(通过移位和掩码操作),并且将该值作为偏移向量的索引值来获取其中第一个存活对象的转发地址,然后再借助标记向量获取内存块中存活对象的数量及大小,并据此增加偏移。
这一操作可以通过查表的方式在常数时间内完成,例如,在图3.3中,对象old在内存块的已标记槽中的偏移量为3,那么该对象的目标地址将是第10个槽,即:offset [block]=7加上offsetInBlock(old)=3。
四、复制式回收
- 标记—清扫回收的开销较低,但其可能受到内存碎片问题的困扰。
在一个设计良好的系统中,垃圾回收通常只会占用整体执行时间的一小部分,赋值器的执行开销将决定整个程序的性能,因此应当设法降低赋值器的开销,特别是应当尽量提升它的分配速度。
- 标记—整理回收器可以根除碎片问题,而且支持极为快速的“阶跃指针”(bump a pointer)分配(见第7章),但它需要多次堆遍历过程,进而显著增加了回收时间。
本章将介绍第三种追踪式回收算法:半区复制(semispace copying)。
回收器在复制过程中会进行堆整理,从而可以提升赋值器的分配速度,且回收过程只需对存活对象遍历一次。其最大的缺点在于,堆的可用空间降低了一半。
每次使用使用一半,会收时存活的对象移入另一半区域(同时会整理在一起),当前使用区域全部回收,另一区域变为使用区域。
4.1 半区复制回收
原理
基本的复制式回收器会将堆划分为两个大小相等的半区 (semispace),分别是 来源空间(fromspace) 和 目标空间(tospace) 。
为了简单起见,算法4.1假定堆是一块连续的内存空间,但这并非强制性要求。当堆空间足够时,在目标空间中分配新对象的方法是根据对象的大小简单地增加空闲指针,如果可用空间不足,则进行垃圾回收。
回收器在将存活对象从来源空间复制到目标空间之前必须先将 两个半区的角色互换 (见算法4.2中的第2行)。在回收过程中,回收器简单地将存活对象从来源空间中迁出;在回收完成后,所有存活对象将紧密排布在目标空间的一端。
在下一轮回收之前,回收器将简单地丢弃来源空间(以及其中的对象),但在实际应用中基于安全考虑,许多回收器在初始化下一轮回收过程之前都会先将该区域清零(见第11章中讨论运行时系统接口的内容)。

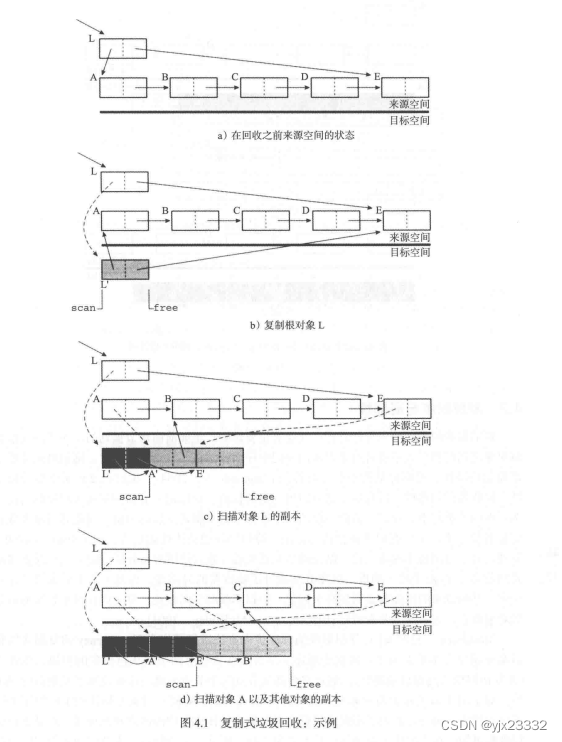
在回收过程的初始化完成之后,半区复制回收器首先将根对象复制到目标空间,并以此来填充工作列表(算法4.2中的第4行)。
当遍历到来源空间中的某一对象时,copy方法首先检查该对象是否已完成迁移(即是否已存在转发地址),如果没有,则将该对象复制到目标空间中指针free所指向的地址,同时根据对象的大小增加指针free(与分配过程类似)。
对于存活对象在目标空间中的对应副本,回收器必须能够保持其原有的拓扑关系,因此当回收器将对象复制到目标空间时,会将其转发地址记录在来源空间内的原有对象中(算法4.2中的第34行)。
forward方法在对目标空间中的域进行扫描时会使用目标对象的转发地址来更新该域,如果目标对象的转发地址尚不存在,则对该对象进行复制(算法4.2中的第22行)。当回收器完成对目标空间中所有对象的扫描时,回收过程结束。
与标—整理回收不同,半区复制回收无须在对象头部中引入额外空间。由于来源空间中的对象在复制完成后便不再使用,所以其每个槽都可以用于记录转发地址(至少在万物静止式回收中如此)。因此复制式回收甚至适用于不包含头部的对象。

4.1.1 工作列表的实现
与其他追踪式回收器类似,半区复制需要一个工作列表来记录待处理对象。工作列表有多种实现方式,每种方式的对象图遍历顺序以及空间需求各不相同。
Fenichel和 Yochelson的策略是将工作列表作为一个简单的辅助栈,十分类似于第二章所描述的标记—清扫回收器所使用的标记栈,当栈为空时,复制过程结束。
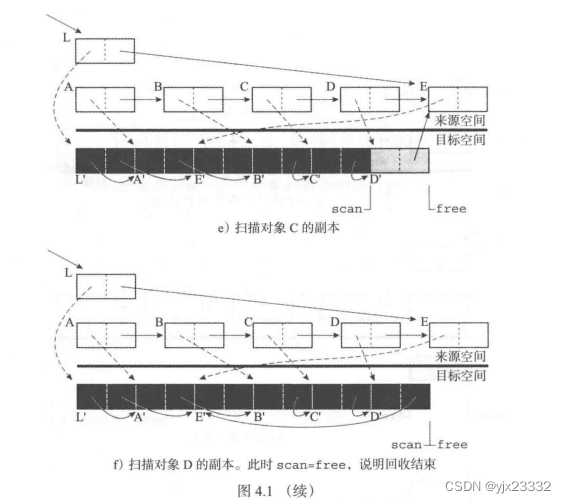
Cheney扫描(Cheney scanning)算法
Cheney提出的一种十分优雅的算法,该算法利用目标空间中的灰色对象实现先进先出队列。该算法仅需要一个指针scan来指向下一个待扫描对象,除此之外不再需要任何额外空间。
-
在半区翻转完成后,指针free和指针scan均指向目标空间的起始地址(见算法4.3中的initialise方法)。
-
完成根对象的复制后,指针scan和指针free之间的灰色对象(已完成复制但未完成扫描)便构成了工作列表。
-
随着目标空间中对象域的扫描以及更新,指针scan 不断向前迭代(见算法4.3中的第9行)。
-
当工作列表为空,也就是指针scan与指针free重合时,回收完成。
该算法的实现非常简单,要确定回收过程是否完成,仅需要通过isEmpty方法判断指针scan和指针free是否重合,remove方法只是简单地返回指针scan,add方法则无须执行任何操作。

4.2 遍历顺序与局部性
赋值器和回收器的局部性对程序性能有重要影响。
启发式方法
以标记—清扫和复制式回收的对比为例:
-
对于空间较小的堆:在同等条件下,标记—清扫回收的可用堆大小是复制式回收的两倍,因此其回收次数会比后者少一半,于是我们可能会认为标记—清扫回收的整体性能更优。
-
对于较大的堆,顺序分配提升了赋值器的局部性,提升了各个层次的缓存命中率,其所带来的性能收益明显高于标记—清扫回收的空间收益。
Cheney的复制式回收器遍历顺序在本质上属于广度优先顺序,尽管其在目标空间中对灰色对象的扫描是线性的(即其访问模式具有可预测性),但是它会将父节点与子节点分离,从而破坏了赋值器的局部性。
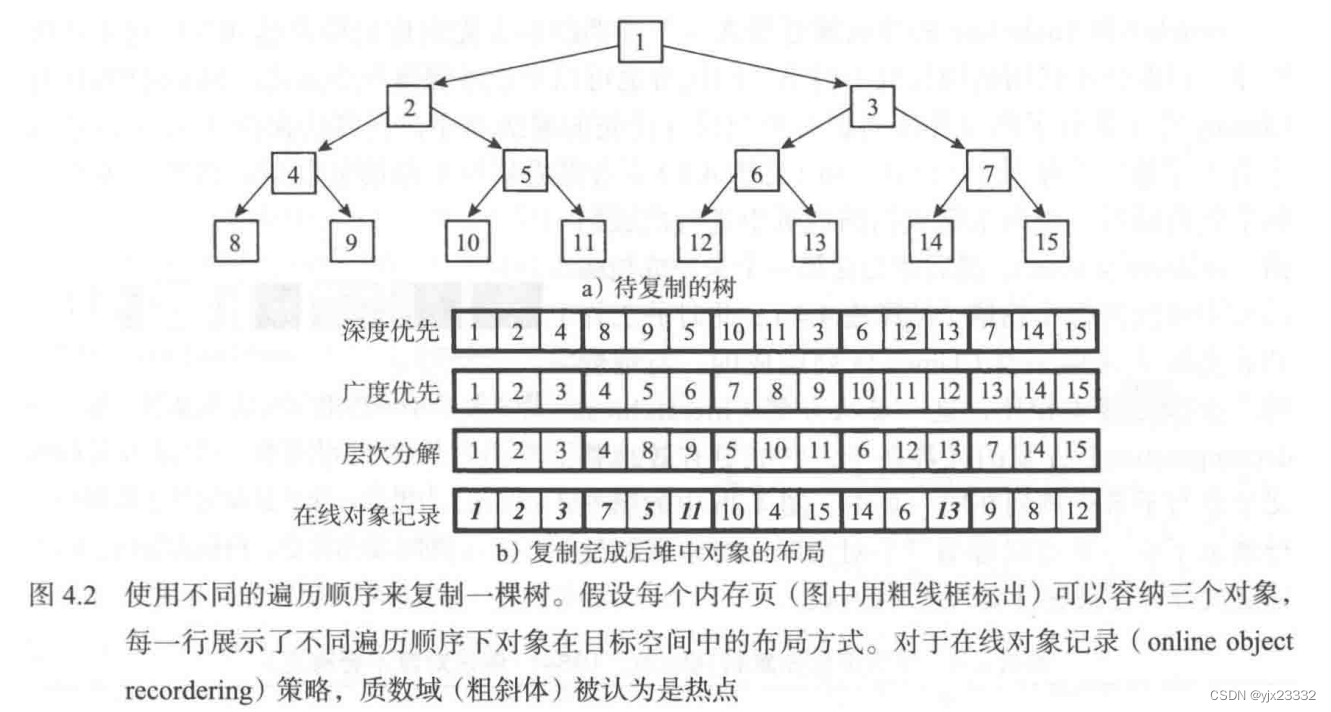
对于图4.2a 所示的对象布局,图4.2b 中的表对比了对同一对象布局使用不同顺序进行遍历的结果,每一行展示了不同遍历顺序下对象在目标空间中的最终排列形式。对第2行进行观察可知,在广度优先顺序下,只有对象2和3距其父节点较近。
复制式回收器和整理式回收器都会移动对象,因此可以潜在地影响赋值器的局部性。
-
对于标记—整理算法而言,滑动顺序通常是最优的,因为它保持了赋值器分配对象时建立的顺序。
-
对于将存活对象迁移到新空间且不破坏原有数据的复制式回收,其可以通过对象的重排列来提升赋值器的局部性。
但是,我们无法找到一个最优的对象布局来最大限度地提升程序的高速缓存命中率,其原因有二:
- 回收器无法预知赋值器未来将会以何种方式访问存活对象
- 其次,Petrank和Rawitz 指出,对象排列问题是一个NP完全问题,也就是说,即使可以完全预知赋值器未来访问对象的次序,也无法找到一个高效算法来计算出最优的排列方式。
NP完全问题
NP的英文全称是Non-deterministic Polynomial的问题,即 多项式 复杂程度的 非确定性 问题。
唯一的办法是使用启发式方法。通过程序过往的行为来预测其未来的行为是一种可行方案。
启发式算法(heuristic algorithm)是相对于 最优化 算法提出的。
-
一些研究者假定程序在不同输人下行为都是相似的,进而采取 在线分析(profiling) 策略,也有研究者假定程序在连续两个时间区间内的行为不会发生变化,进而使用**在线采样(onlinesampling)**策略。
-
另一种启发式方法是保持对象在分配时的顺序,就像滑动整理那样。
-
第三种方法是尝试将子节点靠近它的某个父节点排列,因为访问子节点的唯一途径是经过该节点的一个父节点。Cheney 算法使用广度优先遍历,从而导致具有相关性的对象分离,即趋向于将“远亲”而非父子节点排列在一起, 而深度优先遍历则趋向于将子节点与其父节点排列得更近(图4.2b中的第一行)。
优化深度优先
对于不同复制顺序对赋值器局部性的影响,早期的研究主要集中在减少 缺页异常(page fault) 方面,其目的是将相关对象排列在同一内存页中。
Moon对Chenny算法进行了修改并使其拥有近似深度优先的遍历顺序,新算法在指针scan的基础上引入了第二个指针partialScan (见图4.3)。

Fenchel和Yochelson的算法通过引人一个辅助的后进先出标记栈来达到深度优先遍历顺序,但即使不使用辅助栈且不付出空间代价也可以实现准深度优先遍历。
当完成某一对象的复制后,该算法先在目标空间内最后一个尚未完成扫描的页中进行次级扫描( secondary scan),然后才会在第一个未完成扫描的页中继续进行主扫描(见算法4.4)。此时的工作列表实际,上是由一对Cheney队列组成的。
与纯粹的广度优先搜索相比,这一层次分解(hierarchical decomposition)方案的优势在于,它能更有效地将父节点与子节点排列在同一页中。
图4.2b中的第三行展示了在一页可以容纳三个对象时,对整棵树使用层次分解算法进行复制之后的状态。

Moon的算法最大缺陷在于,它只记录了一对扫描指针,无法区分指针scan和指针free之间的哪些对象已完成扫描,因而有可能将某些对象扫描两次。
Wilson 等 声称Moon的算法重复扫描的比例大概有30%,并对此进行改进。
- 他们为每一页记录指针scan和指针free,从而将工作列表变成所有需要进行部分扫描的块的链表,因此主扫描可以跳过已经完成次级扫描的对象。
为什么广度优先不行
2.6节曾讨论过如何提升标记—清扫回收器标记阶段的性能,其中提到,Cher等指出使用栈来引导的遍历遵从深度优先顺序,但其对高速缓存行的预取却遵从广度优先顺序。
因此一个自然而然的问题便是,是否可以将基于栈的深度优先复制与Cher等的先进先出预取队列相结合?
很遗憾,答案是否定的。
尽管先进先出顺序可以减少高速缓存不命中对复制过程的影响,但它会将父子节点分开,因为只有当对象从预取队列中移除,而不是从栈中移除时,回收器才会访问对象所包含的引用。
我们来考察图4.4中将字符串对象S从栈中弹出的过程:
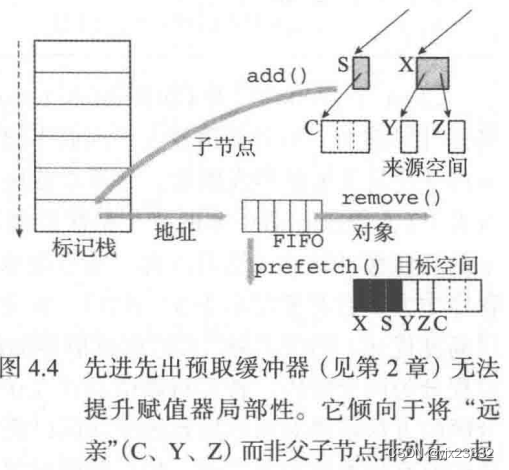
在理想情况下,对象S应当与其相关的字符数组C一起排列在目标空间中,这正是深度优先算法所能达到的效果。
当使用先进先出队列时,S从栈中弹出后将被立即添加到预取队列中,假设此时队列已满,则回收器会将最老的对象X从队列中移除并复制,同时将其引用的对象Y和乙压人栈中。但是,回收器从队列中移除和复制Y和Z将发生在S之后、C之前。
上述各种复制算法的重排列方式都是静态的,即它们都没有考虑具体程序的实际行为,但可以肯定的是,对象重排列方式所能带来的收益最终取决于赋值器的行为。
在线对象记录
Lam等 发现,两种算法都对程序数据结构的组合方式以及形状十分敏感,对于非树形结构,其性能反而会有所降低。
Siegwart和Hirzel也发现,并行层次分解回收器可以提升某些基准测试程序的性能,但对于其他的则几乎没有效果。
为解决这一问题,Huang 等 对程序进行动态分析,并尝试将对象的“热”域与其父节点排列在一起。算法4.5展示了他们的在线对象记录( online object recording) 方法,图4.2b的最后一行展示了其效果。在算法的主扫描循环中(算法4.5中的第6行),回收器在对所有的“冷”域进行处理之前会先处理工作列表中的所有“热”域。
对于一个配备了 方法采样机制(method sampling mechanism) 的自适应动态编译器而言,确定这些域的开销通常很小。
他们的算法也可以通过对“热”域的淘汰与重新扫描来适应程序在不同阶段的行为变化,他们发现在引人该算法后,系统的性能可以达到或者超过了诸如广度优先等静态重排列顺序。


其他方式
Chen等 以及Chilimbi和Larus 各自通过在分代回收器中主动调用回收器来提升局部性,但其开销较大,因而不会经常启用。对于以提升局部性为目标的回收,分配率的变化是主要的触发因素,转译后备缓冲区( translation lookaside buffer, TLB)中的数据或者L2高速缓存命中率的变化是次要触发因素。
他们将得到访问的对象记录在一个固定大小的环状缓冲区中(他们声称,节点级别分析比域级别分析的开销要小5%,因为面向对象程序中大多数对象都小于32字节)。在突发式的采样过程中,他们使用一个开销较大(但经过高度优化)的读屏障日来拦截赋值器加载引用的操作,并据此分辨热对象。热对象复制的过程分为两个阶段:
- 首先将赋值器正在访问的对象复制到一个临时缓冲区中,然后使用层次分解的方法将热对象添加到该缓冲区以提升换页性能。
- 回收器将已复制对象的原有位置标记为空闲,然后将临时缓冲区中经过重排列的对象移动到堆的一端。
该方案尝试在高速缓存性能以及换页行为方面同时进行优化。实验结果表明,将两种优化方法结合的收益通常大于两者各自收益的总和,且对于多数大型C#应用程序而言,平均执行时间都会得到改善。尽管该算法会保留部分垃圾对象,但其总量通常很小。
还有学者提出,可以依照对象类型来进行自定义的静态重排序,特别是对于系统数据结构来说。
- 通过允许类的开发者来决定域的复制顺序,Novark等 显著提升了某些特定数据结构的高速缓存命中率。Shuf等 使用 离线分析(off-line profiling) 的方法来确定 富类型( prolific type) ,他们同时对分配器进行修改,即当创建父对象时为其子对象预留相邻空间,这样既提升了局部性,同时又可以将具有相同生命周期的对象聚集在一起。
对于本节所提到的将先进先出预取队列与深度优先复制相结合所带来的问题,该方案可以在一定程度上予以缓解。
附录
[1]《垃圾回收算法手册 自动内存管理的艺术》
[英]理查德·琼斯(Richard Jones)[美] 安东尼·霍思金(Antony Hosking) 艾略特·莫斯(Eliot Moss)著
王雅光 薛迪 译
最后
以上就是狂野眼睛最近收集整理的关于《垃圾回收算法手册 自动内存管理的艺术》——标记整理与复制式回收(笔记)三、标记—整理回收四、复制式回收附录的全部内容,更多相关《垃圾回收算法手册内容请搜索靠谱客的其他文章。








发表评论 取消回复