【玩转八大排序③】递归版快速排序（Hoare法、挖坑法、前后指针法）

一、快排思想介绍

①基本介绍
 快排的核心思想是分而治之。首先我们任取一个待排序数组中的数作为我们的key值，假设已经我们能够实现将数组中所有小于key的数放在key的左边，所有大于key的数放在key的右边，那么反过来说key值的位置就被确定了。此时我们将数组一分为二——左边的数全部小于等于key值，右边的数全部大于等于key值。

• 上述将数组一分为二的过程就是分而治之思想的体现，我们将大问题分解为小问题，将排序数组的过程转化为每次确定一个数位置的过程，由此最终实现数组的整体有序
• key值的选取可以开头结尾，也可以去中间值，也可以随机取。中间值取法的不同对算法的优劣会产生影响，这在接下来会提到。但我们都先取头值作为我们的key
• 实现小于key值的数放在key值的左边，大于key值的数放在key值的右边的过程是快排算法的难点。它的实现主流的方法有Hoare法，挖坑法，和前后指针法

二、Hoare法介绍

①基本介绍

 Hoare法是以快排的创始人Hoare命名的，也是快排最初的实现版本。其基本思想就是用两个指针分别指向待排序数组的开头和结尾。

• 如果我们取头值作为我们的key值，那么我们一定要让右指针先移动
• 如果我们取尾值作为我们的key值，那么我们一定要让左指针先移动

 所谓“移动”就是如下过程：

• right指针直到找到小于key的值才停下来
• left指针直到找到大于key的值才停下来
• 将left和right所对应的值进行交换。重复上述过程直到两者相遇

②疑难解答

Q1：为什么一定要让right指针先移动
【答】需要注意的是，left和right不是同时相向运动而是有先后顺序的运动。这就意味着right一定会指向最后一个小于key的值，否则被left占了先机就不能保证right会指向最后一个小于key的值
Q2：为什么一定要让right指针指向最后一个小于key的值
【答】因为在最后我们需要将key值和right所指向的值进行交换，也就是说right最后指向的位置就是key值应该所在的位置。

③代码呈现

int PartSort(int* arr, int left, int right)               
{
	int key = arr[left];
	int keyi = left;
	while (left < right)									//(1)
	{
		while (left < right && arr[right] >= key)           //(2)
			right--;
		while (left < right && arr[left] <= key)
			left++;
		swap(&arr[left], &arr[right]);					    //(3)
	}
	swap(&arr[keyi], &arr[right]);				            
	return right;                                           //(4)
}

void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;
	int keyi = PartSort(arr, left, right);         			//(4)
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

④代码剖析

1. 在left小于right之前持续移动left和right，分别找到比key大的值和比key小的值。
2. 注意到数据中可能有多个key，因此arr[left]与arr[right]在于key值比较的时候等于时也要移动。
3. 交换left和right的值，即交换比key大的值和比key小的值
4. key值已经确定了它的位置——right。我们以right为界，将数组一分为二即进行分治的过程

三、挖坑法介绍

①基本介绍

 挖坑法与Hoare法相比并没有性能上的优化，但是它的优势在更好理解，即不用考虑谁先走谁后走的情况。

②过程图解

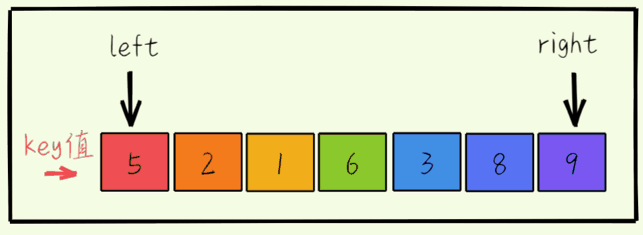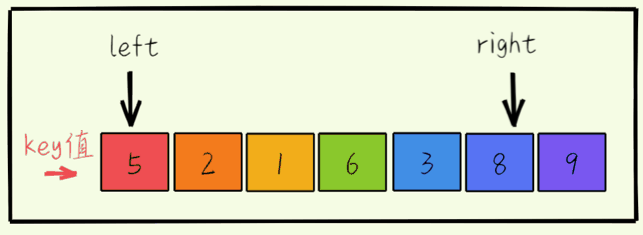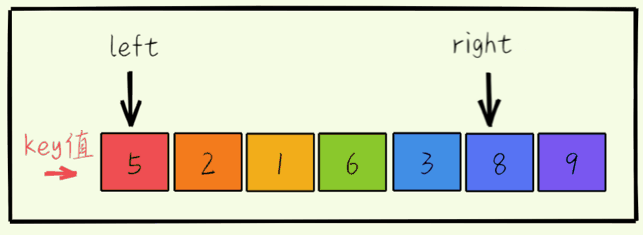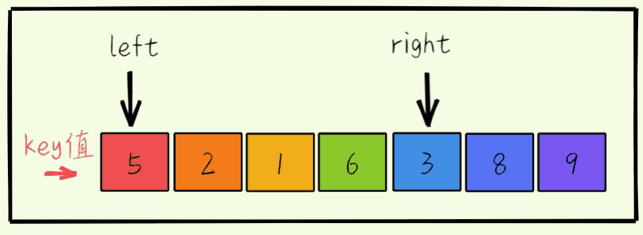
其核心思想就是用一个hole变量存储坑的下标：

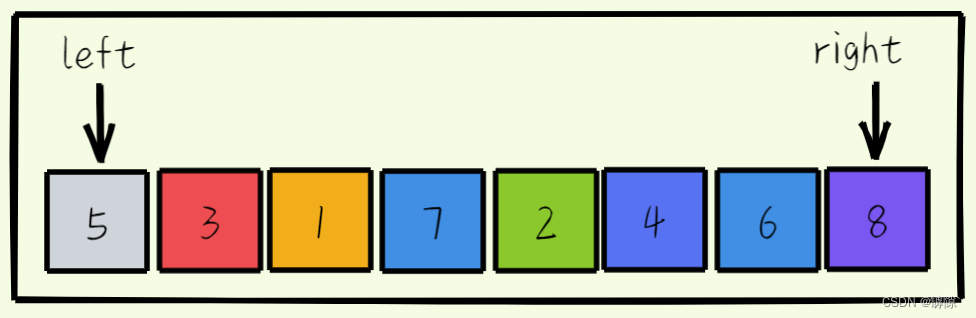
• 初始时我们选第一个元素为坑，并将其值存储在key中，即key为5
  
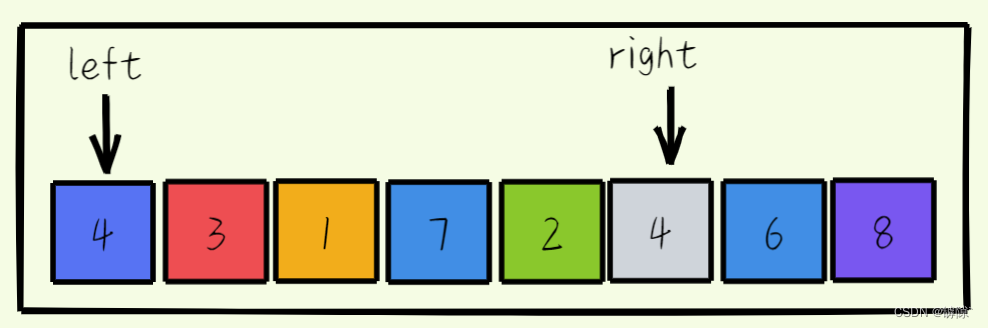
• 右指针向左移动寻找小于key的值。找到后将其填充到hole的位置，相应的原来的位置就变成了hole
  
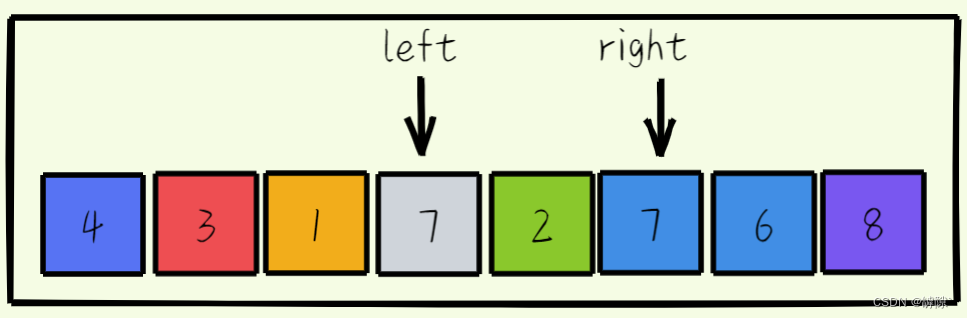
• 左指针向右移动寻找大于key的值。到后将其填充到hole的位置，相应的原来的位置就变成了hole。
  
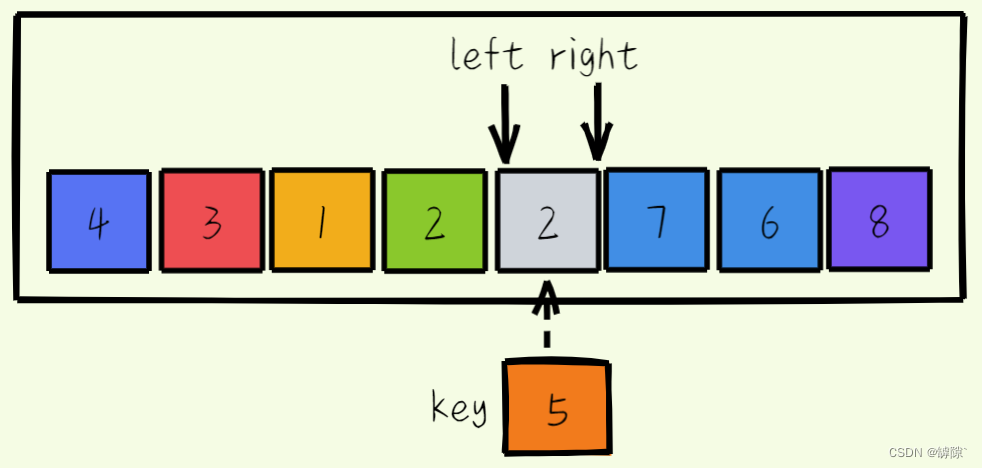
• 最终将key的值填入最后的hole，完成了一次的快排
  

③代码呈现

int PartSort(int* arr, int left, int right)
{
	int hole = left;                                    //(1)
	int key = arr[left];								

	while (left < right)
	{
		while (left < right && arr[right] >= key)
			right--;
		
		arr[hole] = arr[right];
		hole = right;								    //(2)

		while (left < right && arr[left] <= key)
			left++;
		
		arr[hole] = arr[left];
		hole = left;
	}
	arr[hole] = key;                                    //(3)
	return hole;
}

void QuickSort(int* arr, int left, int right)
{
	if (left >= right)
		return;
	int keyi = PartSort(arr, left, right);
	QuickSort(arr, left, keyi - 1);
	QuickSort(arr, keyi + 1, right);
}

④代码剖析

1. 初始时将第一个元素置为hole
2. 对hole位置的更行
3. 最后hole位置就是key应该插入的位置。hole将数组一分为二，所以返回hole的值作为之后区间划分的标准

四、前后指针法介绍

①基本介绍

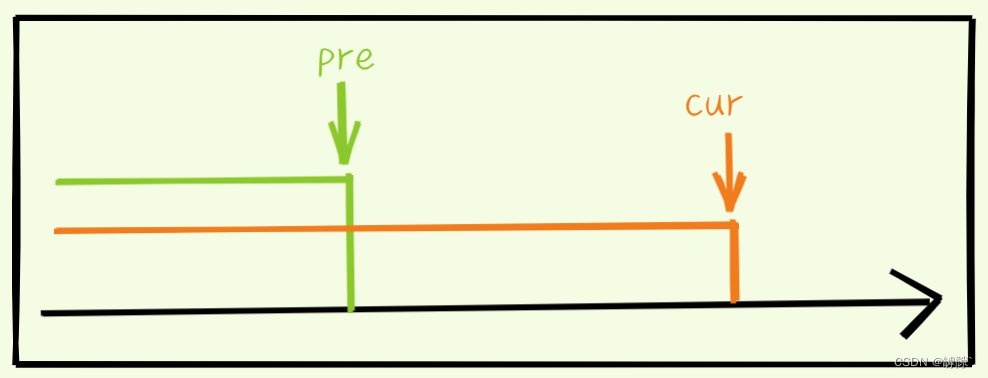
 前后指针法的核心思想是用一对快慢指针维护一个小于key的区间，有点滑动窗口的意味在里面。虽然代码量是最短的，但是理解起来也并不困难

• cur一直往后遍历，当cur遇到小于key的元素时，则将cur处的元素与pre+1处的元素进行交换
• 为什么是pre + 1处的元素呢？因为pre以内的数据（除了头为key）都满足小于等于key的条件
• 当cur遍历结束时pre左边的数据都是小于等于key的，右边都是大于等于key的。最后还需要做的操作是将pre处的数据与left处的数据进行交换，这样就确定了key应该在的位置

②代码呈现

int PartSort(int* arr, int left, int right)
{
	int pre = left;                                   //(1)
	for (int cur = left + 1; cur <= right; cur++)
	{
		if (arr[cur] < arr[left])
			swap(&arr[cur], &arr[++pre]);             //(2)
	}
	swap(&arr[pre], &arr[left]);                      //(3)
	return pre;
}
void Quicksort(int* arr, int left, int right)
{
	if (left >= right)
		return;
	int keyi = Partsort1(arr, left, right);
	Quicksort(arr, left, keyi - 1);
	Quicksort(arr, keyi + 1, right);
}

五、对快排的优化

①key值的取法

①基本概要
 key的取法对快排时间复杂度的影响非常之大。对于完全逆序的数据，快排的时间复杂度为O(N^2),所以可见我们只取开头或者结尾作为key值是不妥的。有以下两种改进方法

• 在下标范围内用random函数取随机值
• 三数取中：头，尾，中间元素中大小居中的那一个

下面展示三数取中的代码：

int GetmidIndex(int* arr, int left, int right)
{
	int mid = left + ((right - left) >> 1);
	if (arr[left] <= arr[right])
	{
		if (arr[mid] < arr[left])
			return left;
		else if (arr[mid] > arr[right])
			return right;
		else
			return mid;
	}
	else
	{
		if (arr[mid] > arr[left])
			return left;
		else if (arr[mid] < arr[right])
			return right;
		else
			return mid;
	}
}

 那么我们之前都以头作为key值的代码是不是废了？其实不是，我们只需要将取中得出的中间值与头值进行交换，就可以完全套用之前的代码了。

②规模较小时的优化

 在数据规模较小时，快排还不如直接插入排序快，所以在数据规模较小时采用插入排序进行排序。但是在release版本下，由于对递归的优化特别大，所以结果没有三数取中那么明显。

最后

以上就是默默烤鸡为你收集整理的【玩转八大排序③】递归版快速排序（Hoare法、挖坑法、前后指针法）的全部内容，希望文章能够帮你解决【玩转八大排序③】递归版快速排序（Hoare法、挖坑法、前后指针法）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。