一、题目描述

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1： 输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100]，排序后，数组变为 [0,1,9,16,100]

示例 2： 输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

二、思路与解法code

法一：暴力排序

最直观的想法，莫过于：每个数平方之后，排个序，美滋滋，代码如下：

class Solution 
{
public:
    vector<int> sortedSquares(vector<int>& nums) 
    {
        for(auto &v:nums)
            v=v*v;
        sort(nums.begin(),nums.end());
        return nums;
    }
};

这个时间复杂度是 O(n + nlogn)， 可以说是O(nlogn)的时间复杂度，但为了和下面双指针法算法时间复杂度有鲜明对比，我记为 O(n + nlog n)。

法二：双指针

数组其实是有序的， 只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

如动画所示：

class Solution 
{
public:
    vector<int> sortedSquares(vector<int>& nums) 
    {
        vector<int> res(nums.size(),0);//和nums同样大小,全部初始化为0
        int idx=nums.size()-1;//从最大的开始检索
        //i为左指针,j为右指针
        int i=0;
        int j=(nums.size()-1);
        for (int i=0,j=nums.size()-1;i<=j;) //注意:i==j是有效的->得放进去
        {
            if(nums[i]*nums[i]>nums[j]*nums[j])
            {
                res[idx--]=(nums[i++]*nums[i]);//注意:i++不要合并到语句中去写！
                cout<<i<<" "<<endl;
            }
            else
            {
                res[idx--]=(nums[j]*nums[j]);j--;
            }
        }
        return res;
    }
};

其他：语法报错

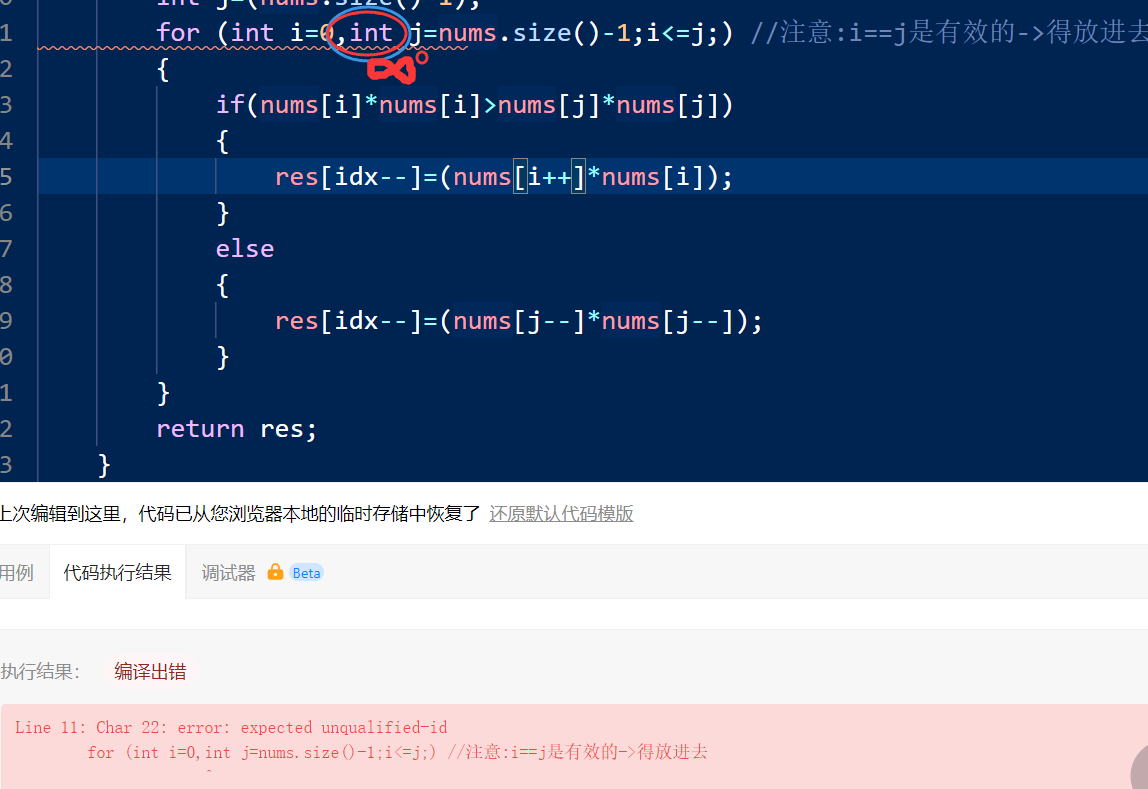
 不可以这么写

 细节：i++不要放在这里面,实际上在乘上下一个nums[i]的时候就已经完成了++运算

最后

以上就是温暖星星为你收集整理的lc[数组]--977.有序数组的平方(双指针)一、题目描述二、思路与解法code法二：双指针其他：语法报错的全部内容，希望文章能够帮你解决lc[数组]--977.有序数组的平方(双指针)一、题目描述二、思路与解法code法二：双指针其他：语法报错所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。