目录

一、二分查找相关

704. 二分查找

34. 在排序数组中查找元素的第一个和最后一个位置[*]

69.x 的平方根

367.有效的完全平方数

528. 按权重随机选择[*]

二、移除元素相关【双指针法】

27. 移除元素

26.删除排序数组中的重复项

283.移动零

977.有序数组的平方

844.比较含退格的字符串

三、滑动窗口法

算法框架（来源：labuladong）

209.长度最小的子数组

904.水果成篮

76. 最小覆盖子串【困难】

 567. 字符串的排列

 3. 无重复字符的最长子串

四、模拟行为相关

59.螺旋矩阵II

54. 螺旋矩阵

五、前缀和

303. 区域和检索 - 数组不可变

304. 二维区域和检索 - 矩阵不可变

 1590. 使数组和能被 P 整除

 面试题 17.05. 字母与数字

六、差分数组

1109. 航班预订统计

1094. 拼车

七、二维数组相关

 48. 旋转图像

八、二分查找进阶题目

1011. 在 D 天内送达包裹的能力[*]

 410. 分割数组的最大值

 875. 爱吃香蕉的珂珂

九、常数时间查找/删除数组元素

380. O(1) 时间插入、删除和获取随机元素

710. 黑名单中的随机数

---

一、二分查找相关

704. 二分查找

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        if (target < nums[left] || target > nums[right]) {
            return -1;
        }      
        while (left <= right) {  
            int midPos = (left + right) / 2;
            int midNum = nums[midPos];
            if (target == midNum) {
                return midPos;
            }
            else if (target < midNum) {
                right = midPos - 1;
            }
            else {
                left = midPos + 1;
            }
        }
        return -1;
    }
};

难点在于区间开闭的确定，我采用的是左闭右闭的区间形式，从而int right = nums.size() - 1，同时循环条件为left <= right。可以举一个奇数列/偶数列的例子，帮助形象理解。

34. 在排序数组中查找元素的第一个和最后一个位置[*]

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int rightBorder = RightBorder(nums, target);
        int leftBorder = LeftBorder(nums, target);
        if (rightBorder == -2 || leftBorder == -2) {
            return { -1, -1 };
        }
        else if (rightBorder - leftBorder >= 0) {
            return { leftBorder , rightBorder };
        }
        else {
            return { -1, -1 };
        }
    }

    int RightBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; 
        int rightBorder = -2;
        while (left <= right) {
            int midPos = (left + right) / 2;
            int midNum = nums[midPos];
            if (target < midNum) {
                right = midPos - 1;
            }
            else {
                left = midPos + 1;
                rightBorder = left;
            }
        }
        return rightBorder;
    }

    int LeftBorder(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int leftBorder = -2;
        while (left <= right) {
            int midPos = (left + right) / 2;
            int midNum = nums[midPos];
            if (target <= midNum) {
                right = midPos - 1;
                leftBorder = right;
            }
            else {
                left = midPos + 1;
            }
        }
        return leftBorder;
    }
};

思路：采用二分法分别查找左边界和右边界。这里与二分法查找单个元素不同的是，若找到（target = midNum）时，不跳出，而是更新目标值的左边界和右边界。

这里采用的是闭区间二分法，可以理解为：不再管之前找到的值了，在新的区间里继续采用二分法，查找新的区间里是否还有目标值。在查找右边界时，若新的区间中没有目标值，意味着target < midNum，从而右边界值不会再被更新了。

69.x 的平方根

class Solution {
public:
    int mySqrt(int x) {
        int left = 0;
        int right = x;
        int res = -1;
        if (x == 0)
        {
            return 0;
        }
        if (x == 1) {
            return 1;
        }
        //保证mid > 0
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (mid <= x / mid) {
                res = mid;
                left = mid + 1;
            }
            else {
                right = mid - 1;
            }
        }
        return res;
    }
};

本题在使用二分法查找时遇到两个问题：

1.函数返回值的选取。用中间变量res记录迭代结果，只要mid<target就更新res，而mid> target则不更新res，这里很类似上题的求右边界。当出现target在二分区间左侧时，之后target将始终处于二分区间左侧直到while条件不成立跳出，且res始终不会被更新。

2.采用mid <= x / mid：避免数乘，否则溢出；int mid = left + (right - left) / 2：避免求和带来的溢出。

367.有效的完全平方数

class Solution {
public:
    bool isPerfectSquare(int num) {
        int left = 0;
        int right = num;
        int res = -1;
        int mid = -1;
        if (num == 1) {
            return true;
        }
        while (left <= right) {
            mid = left + (right - left) / 2;
            if (mid > num / mid) {
                right = mid - 1;
            }
            else {
                left = mid + 1;
                res = mid;
            }
        }
        if (res * res == num) {
            return true;
        }
        return false;
    }
};

本题思路和69一致，所不同的是利用二分法找到符合mid <= num/mid的“右边界”后，应添加res*res == num 的条件进行完全平方数的判断。

528. 按权重随机选择[*]

class Solution {
public:
    Solution(vector<int>& w) {
        // 构造前缀和数组
        this->preSum.resize(w.size(), 0);
        this->preSum[0] = w[0];
        for (int i = 1; i < w.size(); i++) {
            preSum[i] = preSum[i - 1] + w[i];
        }
    }
    int pickIndex() {
        // rand()生成[0,n)的随机数
        int target = rand() % preSum[preSum.size() - 1] + 1;
        return  LeftBound(this->preSum, target);
    }
private:
    vector<int> preSum;
    int LeftBound(vector<int>& preSum, const int target) {
        int left = 0;
        int right = preSum.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (target > preSum[mid]) {
                left = mid + 1;
            }
            else if (target < preSum[mid]) {
                right = mid - 1;
            }
            else if (preSum[mid] == target) {
                return mid;
            }
        }
        return left;
    }
};

本题的技巧在于构造权重值的前缀和数组，通过随机数生成前缀和数组中对应的目标元素（如下图所示，来源：labuladong）：

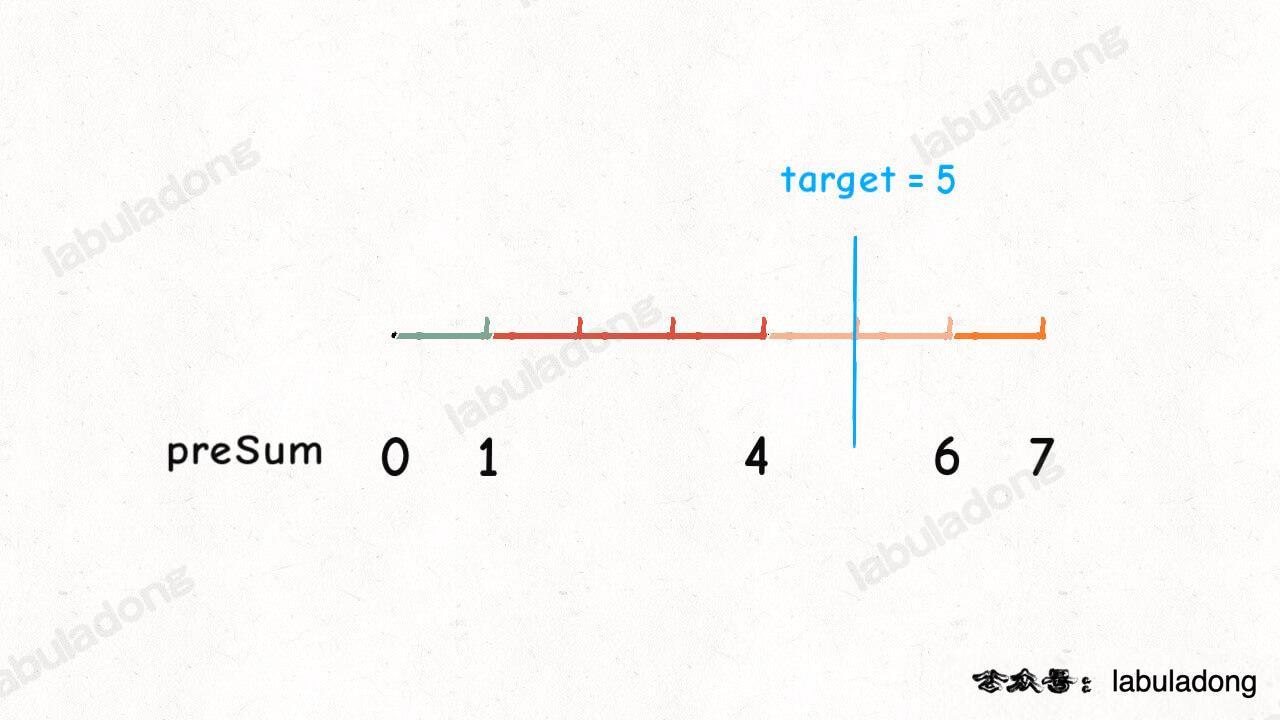
 本题的难点在于查找前缀和数组中，大于等于所生成的随机数的第一个元素。由于前缀和数组是已排序的升序数组，因此可以采用二分法查找。对于目标元素不存在的序列，尤其要明确大于等于该元素的第一个元素，等同于查找左边界【而非右边界！！！】。

当目标元素 target 不存在数组 nums 中时，搜索左侧边界的二分搜索的返回值可以做以下几种解读：

1、返回的这个值是 nums 中大于等于 target 的最小元素索引。

2、返回的这个值是 target 应该插入在 nums 中的索引位置。

3、返回的这个值是 nums 中小于 target 的元素个数。

一个更简单的记忆方式是，若数组中不存在目标元素，退出while循环时left>right，left下标对应元素是大于目标值的元素。 

---

二、移除元素相关【双指针法】

27. 移除元素

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            if (val != nums[fastIndex]) {
                nums[slowIndex++] = nums[fastIndex];
            }
        }
        return slowIndex;
    }
};

 双指针法思想：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。找到目标元素时，慢指针停在目标元素这里不动，快指针先走；直到下次循环时快指针找到非删除元素，并赋值给慢指针指向的位置，此时慢指针才能离开。

由于每次循环结束后，慢指针永远指向符合要求的数组序列的下一个元素，因此直接返回慢指针就是数组的size。该方法保持元素的相对顺序。

26.删除排序数组中的重复项

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int slowIndex = 0;
        for (int fastIndex = 1; fastIndex < nums.size(); fastIndex++) {
            if (nums[slowIndex] != nums[fastIndex]) {
                nums[++slowIndex] = nums[fastIndex];
            }
        }
        return slowIndex + 1;
    }
};

仍采用双指针法，慢指针永远指向目标序列的最后一个元素，因此要返回数组长度时返回值为slowIndex + 1。发现不重复的元素后更新慢指针指向的内容，采用++slowIndex，先让慢指针指向下一个元素，再进行赋值。 

283.移动零

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            if (nums[fastIndex] != 0) {
                nums[slowIndex++] = nums[fastIndex];
                if (fastIndex != slowIndex - 1) {
                    nums[fastIndex] = 0;
                }
            }
        }
    }
};

本题要求把零元素移动到数组末端，因此相比于之前的题目，添加了nums[fastIndex] = 0。另一个需要注意的是该语句只有当slowIndex和fastIndex不相等时才应执行，否则在没有找到非零元素时程序会出错。

977.有序数组的平方

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        vector<int> res(nums.size(), 0);
        int k = nums.size() - 1;
        for (int i = 0, j = k; i <= j;) {
            if (nums[i] * nums[i] < nums[j] * nums[j]) {
                res[k--] = nums[j] * nums[j];
                j--;
            }
            else {
                res[k--] = nums[i] * nums[i];
                i++;
            }
        }
        return res;
    }
};

由于非递减序列中存在负数，本题采用了双指针法的第二种形式，即两个指针分别从两侧向中间移动。需要开辟额外的空间来存储排序后的数组。

844.比较含退格的字符串

class Solution {
public:
    bool backspaceCompare(string s, string t) {
        return rebuildString(s) == rebuildString(t);
    }
    string rebuildString(string str) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < str.size(); fastIndex++) {
            if (str[fastIndex] != '#') {
                str[slowIndex++] = str[fastIndex];
            }
            else if (slowIndex != 0 && str[fastIndex] == '#') {
                slowIndex--;
            }
        }
        return str.substr(0, slowIndex);
    }
};

本题利用双指针法对含退格的字符串进行删除重建操作。当fastIndex指向元素为‘#’时，slowIndex后退，并可利用substr返回处理后的子串。

本题还可以利用栈的操作对字符串进行处理。

---

三、滑动窗口法

算法框架（来源：labuladong）

注意：窗口设置为左闭右开区间[ )。因为这样初始化 left = right = 0 时区间 [0, 0) 中没有元素，但只要让 right 向右移动（扩大）一位，区间 [0, 1) 就包含一个元素 0 了。

/* 滑动窗口算法框架 */
void slidingWindow(string s) {
    unordered_map<char, int> window;
    
    int left = 0, right = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 增大窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

209.长度最小的子数组

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0;
        int i = 0;
        int subLength = 0;
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            while (sum >= target) {
                subLength = j - i + 1;
                result = result < subLength ? result : subLength;
                sum -= nums[i++];
            }
        }
        return result == INT32_MAX ? 0 : result;
    }
};

滑动窗口法可以理解为双指针法的一种，这里利用int result = INT32_MAX，判断是否找到了符合条件的子串。循环体内每次都会移动j指针来增加子串的长度，一旦子串满足要求，就记录子串长度，并利用关键语句sum -= nums[i++]来动态调节子序列的起始位置。

904.水果成篮

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int i = 0;
        int subLength = 0;
        int result = 0;
        map<int, int> types;
        for (int j = 0; j < fruits.size(); j++) {
            types[fruits[j]]++;
            subLength++;
            while (types.size() > 2) {
                types[fruits[i]]--;
                subLength--;
                if (types[fruits[i]] == 0) {
                    types.erase(fruits[i]);
                }
                i++;
            }
            result = subLength > result ? subLength : result;
        }
        return result;
    }
};

本题的不易理解题目的意思，fruits[i]代表的元素是水果的种类标记，而不是种类数量。实际上本题在求只包含两个元素的最长子串长度。

本题采用map容器记录了每种水果的<种类标号，数量>，每次移动滑动窗口右边界时，对应标号水果数量加一，若种类数量超过2个，移动滑动窗口左边界。需要注意左边界移动到位的标准，即左边界对应水果的数量为零时，才算移动到位，从map容器中erase该种类。

后续需要熟练掌握map容器的使用，初始化时其中的int元素默认值为0，因此可以采用types[fruits[j]]++完成初始化和更新数量的操作。

从本题中可已看出滑动窗口的关键点在于：窗口内的值，如何确定右边界，如何确定左边界。

76. 最小覆盖子串【困难】

string minWindow(string s, string t) {
        // need记录所需要的字符，window记录当前窗口内的字符
        unordered_map<char, int> need, window;
        for (auto c : t) {
            need[c]++;
        }
        // 滑动窗口左右界限，[左闭,右开)
        int left = 0, right = 0;
        // 记录最小覆盖子串的区间索引
        int start = 0, length = INT_MAX;
        // 有效字符个数
        int valid = 0;
        while (right < s.size()) {
            // 窗口右侧区间移动逻辑
            char add_c = s[right];
            right++;
            if (need.count(add_c)) {
                window[add_c]++;
                // 判断当前字符是否已满，只有当等于时才能增加有效字符个数
                if (window[add_c] == need[add_c])    valid++;
            }

            // 收集完毕时的左侧窗口移动逻辑
            while (valid == need.size()) {
                // 更新最小覆盖子串结果
                if (right - left < length) {
                    start = left;
                    length = right - left;
                }
                char delete_c = s[left];
                left++;
                if (need.count(delete_c)) {
                    // 只有当前字符删除时整好使得该字符没找全时，才让已找全字符数量减一
                    if (window[delete_c] == need[delete_c]) {
                        valid--;
                    }
                    window[delete_c]--;
                }
            }
        }
        return length == INT_MAX ? "" : s.substr(start, length);
    }

这道题做了一下午，是我做的第一道困难题，人麻了。

用tValueTemp记录是否查找齐全，其中键值可以为负数。更新tValueTemp的记录时，若键值>=0，则右侧边界收纳的元素是必须的，cnt++；同时修改左侧边界时，一般都在满足条件后利用while函数进行。只有tValueTemp的键值>0时，左侧边界去除的字符才不多余。满足最小条件时，左侧边界再左移一位，从而完成收缩过程，右侧边界继续下一次扩张。

 567. 字符串的排列

bool checkInclusion(string s1, string s2) {
        unordered_map<char, int> window, need;
        for (auto c : s1) {
            need[c]++;
        }
        int left = 0, right = 0;
        int valid = 0;
        while (right < s2.size()) {
            char add_c = s2[right];
            // 移动右边界，右边界为开区间
            right++;
            // 右边界移动逻辑
            if (need.count(add_c)) {
                window[add_c]++;
                if (window[add_c] == need[add_c]) {
                    valid++;
                    if (valid == need.size()) {
                        return true;
                    }
                }
            }
            // 左边界移动逻辑。移动条件为窗口长度大于子串长度，每次移动一个单位，可以用if
            if (right - left >= s1.size()) {
                char delete_c = s2[left];
                left++;
                if (need.count(delete_c)) {
                    if (window[delete_c] == need[delete_c]) {
                        valid--;
                    }
                    window[delete_c]--;
                }
            }
        }
        return false;
    }

 注意滑动窗口框架的使用。

 3. 无重复字符的最长子串

int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> window;
        int left = 0, right = 0;
        // 考虑到空字符串的情况，res初始值设置为0
        int res = 0;
        while (right < s.size()) {
            // 移动右边界
            char add_c = s[right];
            window[add_c]++;
            right++;
            // 移动左边界
            if (window[add_c] > 1) {
                while (window[add_c] > 1) {
                    char delete_c = s[left];
                    window[delete_c]--;
                    left++;
                }
            }
            // 无重复元素，更新结果
            else {
                res = max(res, right - left);
            }
        }
        return res;
    }

---

四、模拟行为相关

59.螺旋矩阵II

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n, vector<int>(n, 0));
        //每次循环的起始位置
        int startX = 0;
        int startY = 0;
        //循环的次数
        int loop = n / 2;
        //若n为奇数，单独对中间元素赋值
        int mid = n / 2;
        int i, j;
        //待填充数字
        int num = 1;
        //每次循环填充的格数
        int offset = 1;
        //每次循环包括四步：上方从左到右，右侧从上到下，下方从右到左，左侧从下到上
        //循环区间都是左闭右开
        while (loop--)
        {
            //i为行坐标，j为列坐标，开始循环
            i = startX;
            j = startY;
            for (; j < n - offset ; j++) {
                res[i][j] = num++;
            }
            for (; i < n - offset; i++) {
                res[i][j] = num++;
            }
            for (; j > startY; j--) {
                res[i][j] = num++;
            }
            for (; i > startX; i--) {
                res[i][j] = num++;
            }
            startX++;
            startY++;
            offset++;
        }
        //n为奇数时给最中间的格子赋值
        if (n % 2 != 0) {
            res[mid][mid] = num;
        }
        return res;
    }
};

模拟行为时，需要理清循环流程，划清每次循环的判别条件。例如本题中填充一圈（即一次循环）分为四个部分，每个部分都采用左闭右开的区间，保证了循环的对称性，易于编写代码。

54. 螺旋矩阵

vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res;
        // 起始和终止边界
        int x_begin = 0;
        int x_end = matrix[0].size() - 1;
        int y_begin = 0;
        int y_end = matrix.size() - 1;
        // 结果矩阵没有满时，模拟行为进行遍历
        while (res.size() < matrix.size() * matrix[0].size()) {
            // 水平向右
            if (y_begin <= y_end) {
                for (int i = x_begin; i <= x_end; i++) {
                    res.push_back(matrix[y_begin][i]);
                }
                y_begin++;
            }
            // 竖直向下
            if (x_begin <= x_end) {
                for (int j = y_begin; j <= y_end; j++) {
                    res.push_back(matrix[j][x_end]);
                }
                x_end--;
            }
            // 水平向右
            if (y_begin <= y_end) {
                for (int i = x_end; i >= x_begin; i--) {
                    res.push_back(matrix[y_end][i]);
                }
                y_end--;
            }
            // 竖直向上
            if (x_begin <= x_end) {
                for (int j = y_end; j >= y_begin; j--) {
                    res.push_back(matrix[j][x_begin]);
                }
                x_begin++;
            }
        }
        return res;
    }

本题尤其需要注意四步模拟的进行条件。 

---

五、前缀和

前缀和主要适用的场景是原始数组不会被修改的情况下，频繁查询某个区间的累加和。

303. 区域和检索 - 数组不可变

class NumArray {
public:
    NumArray(vector<int>& nums) {
        this->my_nums = nums;
        this->accumulate_nums.resize(nums.size() + 1, 0);
        for (int i = 1; i <= nums.size(); i++) {
            this->accumulate_nums[i] = this->accumulate_nums[i - 1] + this->my_nums[i - 1];
        }
    }

    int sumRange(int left, int right) {
        return this->accumulate_nums[right + 1] - this->accumulate_nums[left];
    }

private:
    vector<int> my_nums;
    vector<int> accumulate_nums;
};

 new 一个新的数组 preSum 出来，preSum[i] 记录 nums[0..i-1] 的累加和。

如果想求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。

304. 二维区域和检索 - 矩阵不可变

class NumMatrix {
public:
    NumMatrix(vector<vector<int>>& matrix) {
        this->my_matrix = matrix;
        this->accumulate_matrix.resize(matrix.size() + 1, vector<int>(matrix[0].size() + 1, 0));
        for (int i = 1; i <= matrix.size(); i++) {
            for (int j = 1; j <= matrix[0].size(); j++) {
                this->accumulate_matrix[i][j] = this->accumulate_matrix[i - 1][j] + this->accumulate_matrix[i][j - 1] +
                                                this->my_matrix[i - 1][j - 1] - this->accumulate_matrix[i - 1][j - 1];
            }
        }
    }
    int sumRegion(int row1, int col1, int row2, int col2) {
        return this->accumulate_matrix[row2 + 1][col2 + 1] - this->accumulate_matrix[row2 + 1][col1] -
                this->accumulate_matrix[row1][col2 + 1] + this->accumulate_matrix[row1][col1];
    }
private:
    vector<vector<int>> my_matrix;
    vector<vector<int>> accumulate_matrix;
};

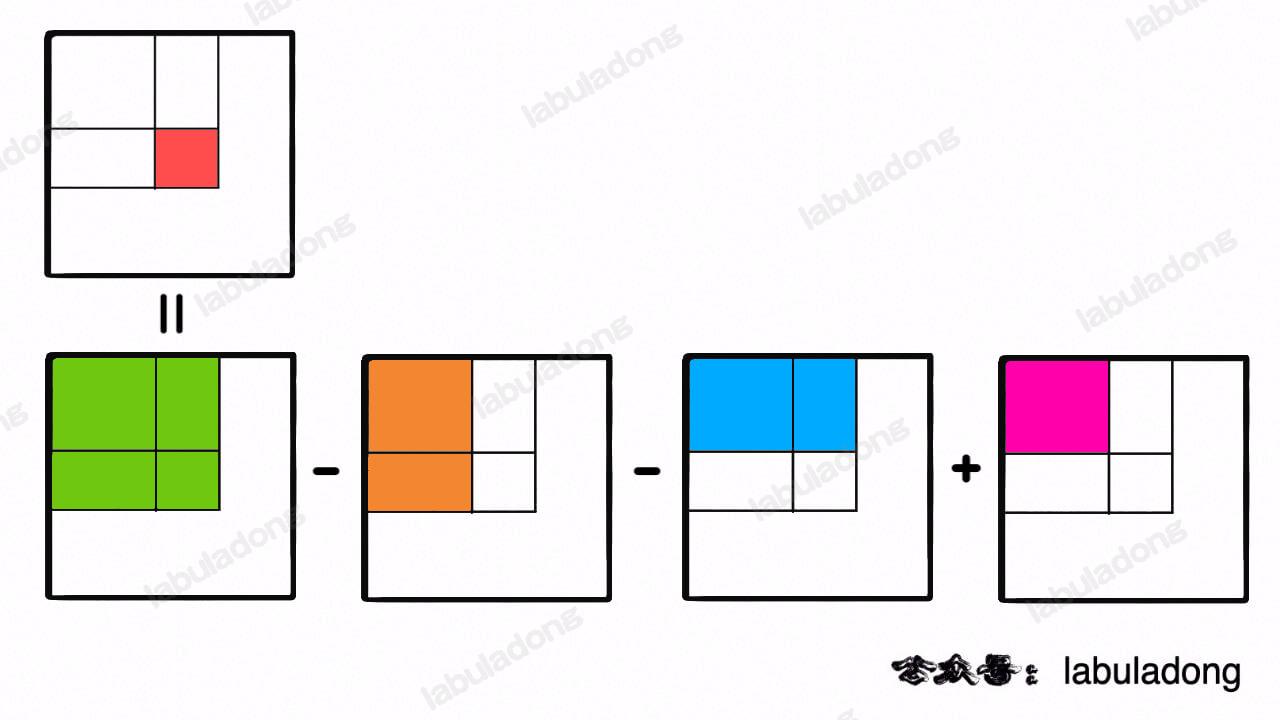
任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算（来源：labuladong）：

 1590. 使数组和能被 P 整除

    // 不能使用双指针法：使用双指针需要满足单调性
    int minSubarray(vector<int>& nums, int p) {
        int n = nums.size(), ans = n;
        vector<int> pre_sum(n + 1);
        pre_sum[0] = 0;
        for (int i = 0; i < n; ++i)
            pre_sum[i + 1] = (pre_sum[i] + nums[i]) % p;
        if (pre_sum[n] == 0) return 0;

        // last记录 s[i] mod p 最近一次出现的下标
        unordered_map<int, int> last;
        for (int i = 0; i <= n; ++i) {
            last[pre_sum[i]] = i;
            // 去掉子数组后能被p整除，意味着去掉的子数组mod p == pre_sum[n]
            // 处理取模的技巧：避免判断pre_sum[i] - x为负数，最终结果落到[0,p)内
            auto it = last.find((pre_sum[i] - pre_sum[n] + p) % p);
            if (it != last.end())
                ans = min(ans, i - it->second);
        }
        return ans < n ? ans : -1;
    }

参考链接 

子数组和问题都可以考虑前缀和。同时为避免溢出，通常会采用一些操作，如取余。 

前缀和+哈希表，可以将O(n^2)复杂度转化为O(n)复杂度。

 面试题 17.05. 字母与数字

    vector<string> findLongestSubarray(vector<string>& array) {
        // 问题转化为：找到一个最长子数组，其元素和等于 0
        // 「元素和等于 0」==「两个前缀和之差等于 0」==「两个前缀和相同」
        int n = array.size();
        vector<int> count(n + 1, 0);
        vector<string> res;
        // 哈希表：前缀和 | 下标
        unordered_map<int, int> record;
        record[0] = 0;
        int start = 0, end = 0;
        for (int i = 0; i < n; ++i) {
                count[i + 1] = count[i] + (array[i][0] >> 6 & 1) * 2 - 1;
            if (record.find(count[i + 1]) != record.end()) {
                if (i - record[count[i + 1]] + 1 > end - start) {
                    start = record[count[i + 1]];
                    end = i + 1;
                }
            }
            else
                record[count[i + 1]] = i + 1;
        }
        return vector<string>(array.begin() + start, array.begin() + end);
    }

 前缀和+哈希表参考题目​​​​​​

---

六、差分数组

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。差分数组diff[i] 就是 nums[i] 和 nums[i-1] 之差（来源：labuladong）。

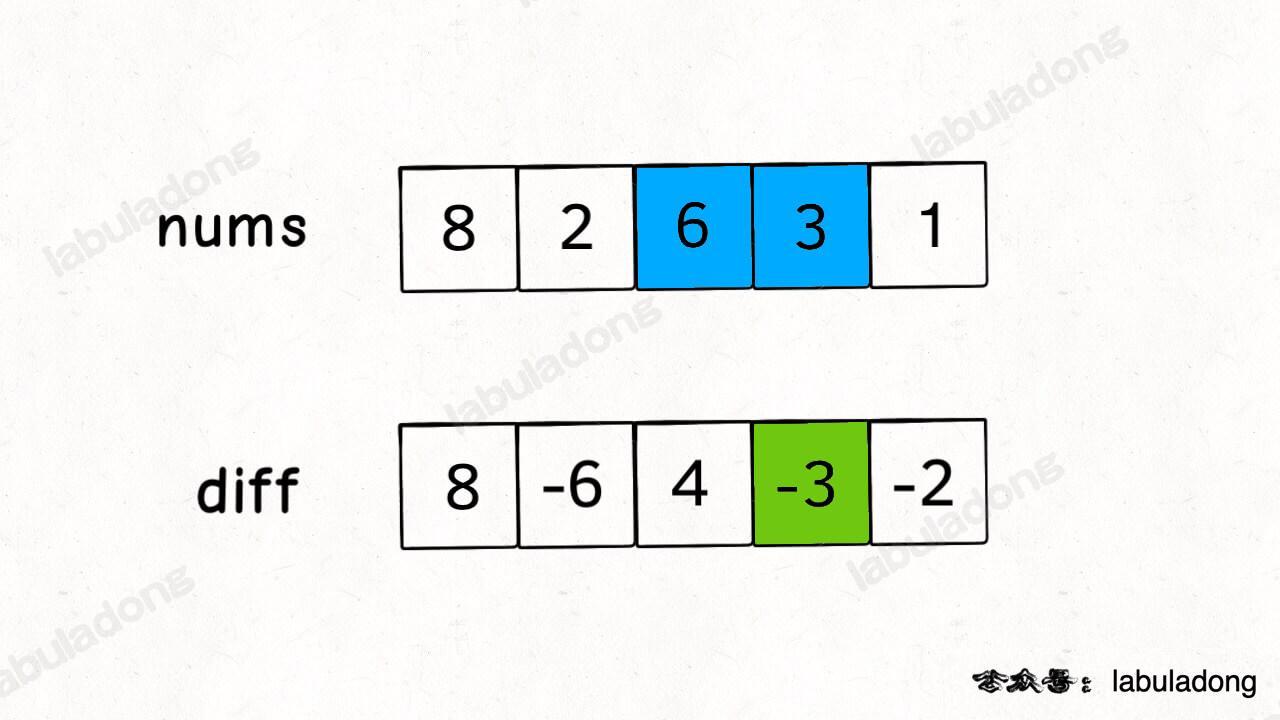
这样构造差分数组 diff，就可以快速进行区间增减的操作，如果想对区间 nums[i..j] 的元素全部加 3，那么只需要让 diff[i] += 3，然后再让 diff[j+1] -= 3 即可。

1109. 航班预订统计

vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        // res是一个差分数组
        vector<int> res(n, 0);
        for (auto booking : bookings) {
            Increase(res, booking[0], booking[1], booking[2]);
        }
        // 将差分数组恢复为预定结果
        for (int i = 1; i < res.size(); i++) {
            res[i] += res[i - 1];
        }
        return res;
    }
    // 差分数组技巧
    void Increase(vector<int>& v, int i, int j, int num) {
        // 航班号转化为数组下标
        i--;    j--;
        // 目标区间第一个元素，差分数组的值增加num；i至j区间内元素大小关系不变；第j+1个差分数组元素的值减小num
        v[i] += num;
        if (j + 1 < v.size()) {
            v[j + 1] -= num;
        }
        return;
    }

1094. 拼车

bool carPooling(vector<vector<int>>& trips, int capacity) {
        // 0 <= fromi < toi <= 1000
        vector<int> trip_length(1001, 0);
        for (auto trip : trips) {
            Increase(trip_length, trip[1], trip[2], trip[0]);
        }
        for (int i = 0; i < trip_length.size(); i++) {
            if (i != 0)    trip_length[i] += trip_length[i - 1];
            if (trip_length[i] > capacity)   return false;
        }
        if (trip_length[trip_length.size() - 1] != 0)  return false;
        return true;
    }
    void Increase(vector<int>& v, int i, int j, int num) {
        // 目标区间第一个元素，差分数组的值增加num；i至j区间内元素大小关系不变
        v[i] += num;
        // 第j站下车，j下标就要减去num
        if (j < v.size()) {
            v[j] -= num;
        }
        return;
    }

---

七、二维数组相关

 48. 旋转图像

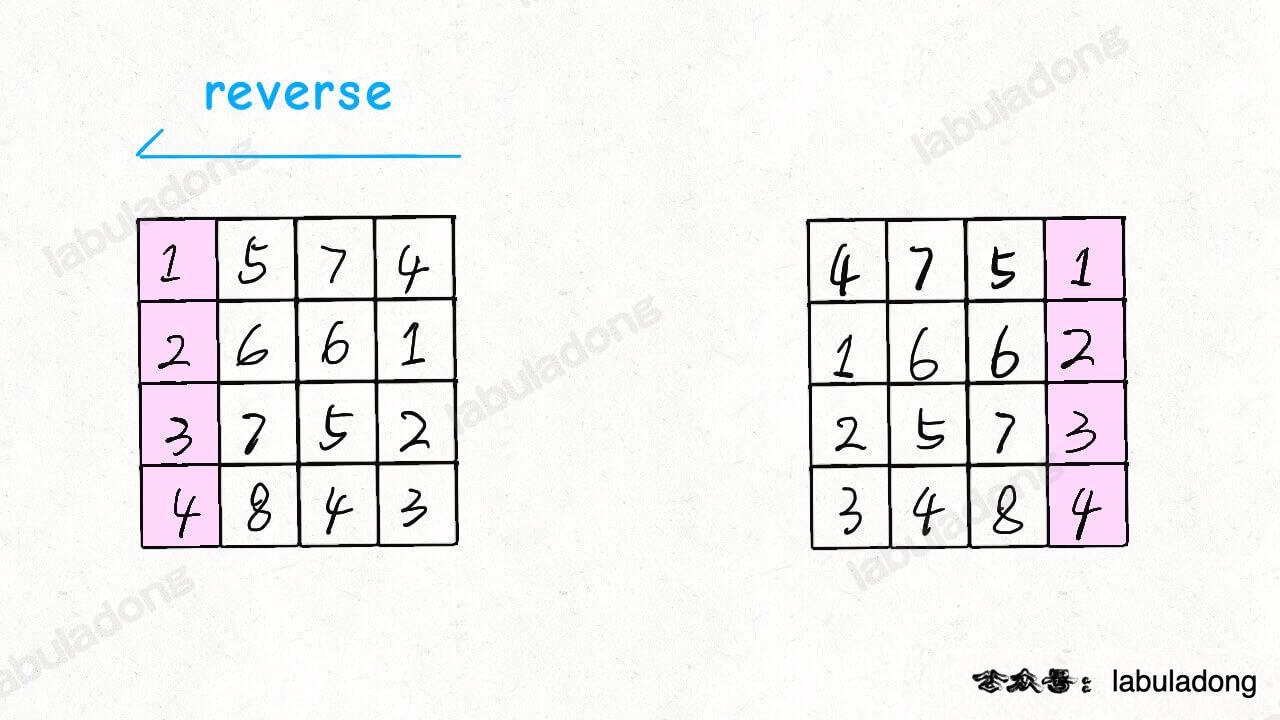
void rotate(vector<vector<int>>& matrix) {
        // 90°旋转可以转换为：沿对角线镜像对称->反转单行元素
        for (int i = 0; i < matrix.size(); i++) {
            for (int j = i + 1; j < matrix[0].size(); j++) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
        for (int i = 0; i < matrix.size(); i++) {
            reverse(matrix[i].begin(), matrix[i].end());
        }
        return;
    }

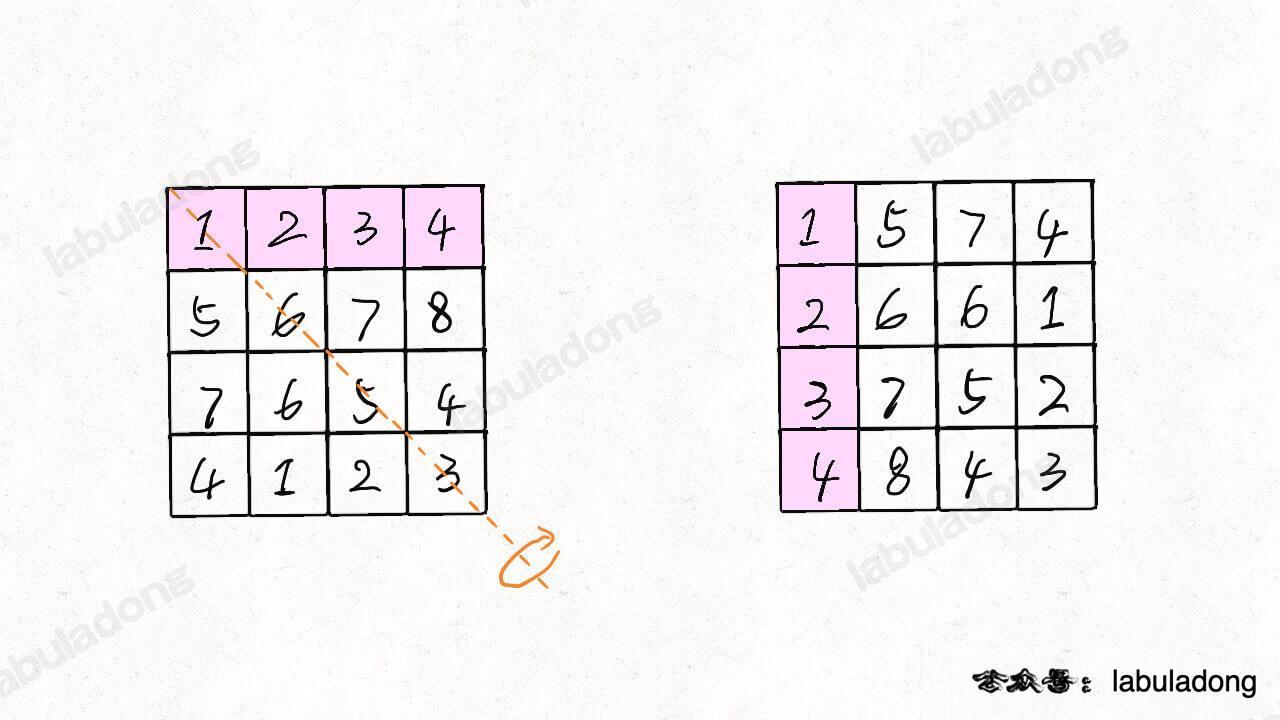
90°旋转可以转换为：沿对角线镜像对称->反转单行元素（如下图所示，来源：）：

---

八、二分查找进阶题目

想要用二分搜索算法解决问题，分为以下几步：

1、确定 x, f(x), target 分别是什么，并写出函数 f 的代码。

2、找到 x 的取值范围作为二分搜索的搜索区间，初始化 left 和 right 变量。

3、根据题目的要求，确定应该使用搜索左侧还是搜索右侧的二分搜索算法，写出解法代码。

1011. 在 D 天内送达包裹的能力[*]

// 找x满足约束条件f(x) == target的最小值，f(x)单调递减，为找左边界
    int shipWithinDays(vector<int>& weights, int days) {
        // 运载能力的左右边界分别是：货物最重者/货物重量和
        int left = 0, right = 0;
        for (int w : weights) {
            left = max(left, w);
            right += w;
        }
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (GetDays(weights, mid) <= days) {
                right = mid - 1;
            }
            else {
                left = mid + 1;
            }
        }
        return left;
    }
    // 定义f：运载能力为x时，需要运货天数为f(x)
    int GetDays(vector<int> weights, int x) {
        int days = 0;
        int capacity = 0;
        for (auto w : weights) {
            if (capacity + w <= x) {
                capacity += w;
            }
            else {
                days++;
                capacity = w;
            }
        }
        // 最后一船的货需要一天
        return days + 1;
    }

x：船的运载能力；f(x):运输天数（和运载能力成反比）；target ：运输天数 D。（如下图所示：来源：labuladong）

 410. 分割数组的最大值

// target:子数组数量限制，f(x)单调减，查找左边界
    int splitArray(vector<int>& nums, int m) {
        // 子数组和的左右区间分别是最大元素/元素和
        int left = *max_element(nums.begin(), nums.end());
        int right = accumulate(nums.begin(), nums.end(), 0);
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (GetSplitNum(nums, mid) <= m) {
                right = mid - 1;
            }
            else {
                left = mid + 1;
            } 
        }
        return left;
    }
    // 获取max_sum下的子数组数量，x：最大子数组和，f(x)：划分子数组数量
    int GetSplitNum(vector<int>& nums, int max_sum) {
        int res = 0;
        int temp_sum = 0;
        for (int num : nums) {
            if (temp_sum + num <= max_sum) {
                temp_sum += num;
            }
            else {
                res++;
                temp_sum = num;
            }
        }
        // 最后还剩下一个未返回结果的子数组
        return res + 1;
    }

「使……最大值尽可能小」是二分搜索题目常见的问法。本题与上一题十分类似，把横坐标换成子数组最大和，纵坐标换成划分个数即可。

 875. 爱吃香蕉的珂珂

// target:时长限制，f(x)单调减，查找左边界
    int minEatingSpeed(vector<int>& piles, int h) {
        // 子数组和的左右区间分别是1 / 数组最大元素
        int left = 1;
        int right = *max_element(piles.begin(), piles.end());
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (GetTime(piles, mid) <= h) {
                right = mid - 1;
            }
            else {
                left = mid + 1;
            }
        }
        return left;
    }
    // 获取speed下的吃光时间，x：吃香蕉速度，f(x)：吃光用时
    long GetTime(const vector<int>& piles, int speed) {
        long res = 0;
        for (auto pile : piles) {
            // 向上取整计算吃光时间
            if (pile % speed == 0) {
                res += pile / speed;
            }
            else {
                res += pile / speed + 1;
            }
        }
        return res;
    }

本题需要注意GetTime函数中res的类型， 防止数据溢出。

---

九、常数时间查找/删除数组元素

380. O(1) 时间插入、删除和获取随机元素

class RandomizedSet {
public:
    RandomizedSet() {

    }

    bool insert(int val) {
        if (this->val_index.count(val))  return false;
        else {
            this->vals.push_back(val);
            this->val_index.insert(make_pair(val, this->val_index.size()));
        }
        return true;
    }

    bool remove(int val) {
        // 交换到尾部，进行尾删
        if (this->val_index.count(val)) {
            int index = val_index[val];
            // 数组最后一个元素下标改为index
            val_index[vals.back()] = index;
            // 交换目标元素和尾部元素，进行尾删
            swap(vals[index], vals.back());
            vals.pop_back();
            // 删除目标元素在下标数组中的索引
            val_index.erase(val);
            return true;
        }
        else    return false;
    }

    int getRandom() {
        return vals[rand() % vals.size()];
    }
private:
    vector<int> vals;
    unordered_map<int, int>  val_index;
};

如果想「等概率」且「在 O(1) 的时间」取出元素，一定要满足：底层用数组实现，且数组必须是紧凑的。

 对数组尾部进行插入和删除操作不会涉及数据搬移，时间复杂度是 O(1)。如果想在 O(1) 的时间删除数组中的某一个元素 val，可以先把这个元素交换到数组的尾部，然后再 pop 掉。利用一个map记录元素的下标，用于查找和交换到数组末尾。【只用一个map的话无法实现常数时间随机访问】

710. 黑名单中的随机数

class Solution {
public:  
    Solution(int n, vector<int>& blacklist) {
        this->val_size = n - blacklist.size();
        // 标记一下黑名单元素，为后续映射做准备
        for (int num : blacklist) {
            black_index[num] = 666;
        }
        int last = n - 1;
        for (int num : blacklist) {
            // 已经在尾部，不需要进行映射
            if (num >= val_size)  continue;
            // 把黑名单元素映射到尾部的元素
            while (black_index.count(last))  last--;
            black_index[num] = last;
            last--;
        }
    }

    int pick() { 
        int val = rand() % this->val_size;
        // 若命中黑名单，映射到数组前部非黑名单元素
        if (black_index.count(val)) {
            return black_index[val];
        }
        return val;
    }
private:
    int val_size;
    unordered_map<int, int> black_index;
};

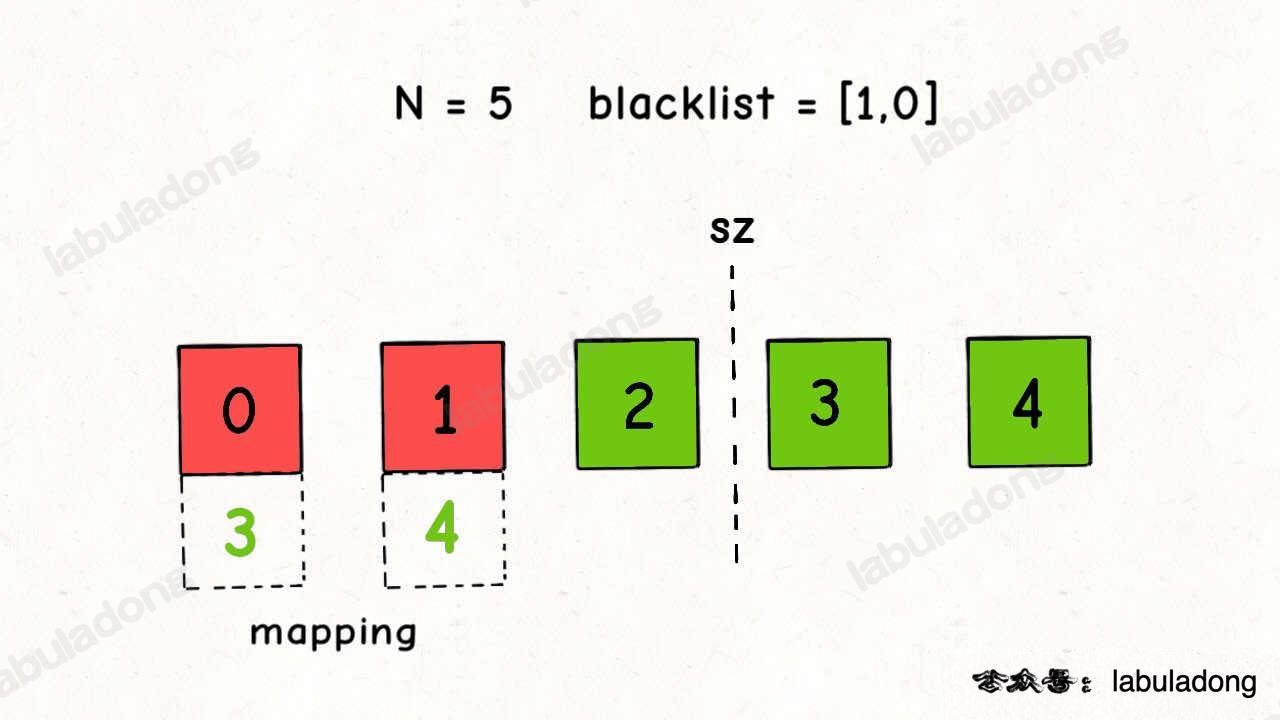
本题思路如下图所示（来源：labuladong），把黑名单元素全部映射到尾部，只取前n-blacklist.size()的元素。需要保证两点：1.映射到的尾部元素不是黑名单元素；2.若该黑名单元素已在尾部，跳过即可。 

最后

以上就是高兴纸飞机为你收集整理的LeetCode 题解随笔：数组篇一、二分查找相关二、移除元素相关【双指针法】三、滑动窗口法四、模拟行为相关五、前缀和六、差分数组七、二维数组相关八、二分查找进阶题目九、常数时间查找/删除数组元素的全部内容，希望文章能够帮你解决LeetCode 题解随笔：数组篇一、二分查找相关二、移除元素相关【双指针法】三、滑动窗口法四、模拟行为相关五、前缀和六、差分数组七、二维数组相关八、二分查找进阶题目九、常数时间查找/删除数组元素所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。