1. 首页
  2. 文章中心
  3. 数据结构

利用easyX图形库画迷宫问题的路径前言

71 阅读 0 评论
我是靠谱客的博主 任性唇膏，最近开发中收集的这篇文章主要介绍利用easyX图形库画迷宫问题的路径前言，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

文章目录

  • 前言
    • 1、迷宫问题
      • 1.1 问题描述：
      • 1.2 实验目的：
    • 2、函数原型及功能
    • 3、关键内容
      • 3.1 如何记录bfs算法访问各个路径中点的横纵坐标
      • 3.2 如何用VC6.0输出最短路径图
      • 3.3 链式队列的基本操作
      • 3.4 宽度优先搜索算法
      • 3.5 递归保存最短路径中点的坐标
    • 4、实验截图

前言

源码链接：https://pan.baidu.com/s/1knFlet0pNWNs07wbTJ4JIQ
提取码：kfkx

复制这段内容后打开百度网盘手机App，操作更方便哦
数据结构课设上抽到了迷宫问题，所以想记录一下完成的过程。编辑器是Visual c++ 6.0（说起这个就一把辛酸泪啊。。。

老师说要把最短的路径画出来，用easyX图形库就可以画。于是我就去网上找“如何在codeblocks上运用easyX图形库”，网上有各种各样的什么环境配置之类的，把这些搞好了之后发现根本用不了，问了周围同学也是用不了（关键是配置过程中还有点艰难，当然很大部分原因是我太菜了/(ㄒoㄒ)/~~

当然这过程中我也去了解了ege图形库，最后的最后，我看到了这条信息(* ￣︿￣)，倔强的我最后还是低头去安装了visual c++ 6.0。

在这里插入图片描述

提示：以下是本篇文章正文内容，下面案例可供参考

1、迷宫问题

1.1 问题描述：

设计一个二维平面图形，设置通路和墙，求从入口到出口的最短路径。迷宫中只有‘0’和‘1’两个数值，‘0’表示通路，‘1’表示墙，有上、下、左、右、左上、左下、右上、右下八个方向可以走。写出一个程序能判断是否可以走出迷宫，如可以走出迷宫，则输出最短路径，否则输出“不能走出迷宫”。

1.2 实验目的：

一是用随机算法解决自动生成一个迷宫，也可手动实时输入迷宫；
二是解决入口和出口的坐标问题，可默认入口为左上角出口为右下角，也可手动实时输入入口和出口坐标；
三是用程序判断是否能走出迷宫，能则输出迷宫最短路径图，不能则指出；
四是程序能满足人机交互的功能。

2、函数原型及功能

1、main( )
原型：int main( )
功能：主调函数。其主要功能，一是完成待输入数据的收集，二是分别调用各个函数

2、input( )
原型：void input(int **maze)
功能：完成迷宫二维数组maze[ ][ ]的输入数据，体现了人机交互特点，既能电脑自动生成数据，也能手动输入数据
3、bfs( )

原型：void bfs(int bx,int by,int ex,int ey,int **maze,int &sum,Queue *queue)
功能：运用宽度优先搜索算法对迷宫进行搜索，一开始将入口坐标加入队列，搜索是否能走出迷宫，sum记录最短路径的步数，并记录搜索过程中的路径坐标

4、print( )
原型：void print(int bx,int by,int xx,int yy,int &j)
功能：递归输出最短路径，从出口开始向前递归，如果当前访问点为入口，则退出函数

5、image( )
原型：void image(int &j,int **maze)
功能：用easyx图形库的line( )函数和circle( )函数画出最短路径图

6、Init( )
原型：void Init(Queue *q)
功能：初始化队列q

7、QueueEmpty ( )
原型：bool QueueEmpty (Queue *q)
功能：判断队列q是否为空，如果为空，则返回1，否则返回0

8、EnQueue( )
原型：void EnQueue(Node &no,Queue *q)
功能：将结构体no加入队列q，完成队列的入队操作

9、DeQueue( )
原型：Node DeQueue(Queue *q)
功能：取队列q中的队头元素并回收空间，返回队头元素，完成队列的出队操作

10、DestroyQueue( )
原型：void DestroyQueue(Queue* q)
功能：销毁队列，释放内存，防止内存泄露

3、关键内容

头文件和结构体如下：

#include <iostream>
#include <ctime>  //随机算法
#include <easyx.h> //图形库
#include <TCHAR.H>   //easyx数字转字符
#include <conio.h>//getch()函数头文件
#include <string.h> //memset的头文件
#include <cstdlib>  //随机函数rand()的头文件
using namespace std;

typedef struct Node  
{
    int x,y;  //记录某点的行数和列数
    int step;  //记录从起点到该点的步数
}Node;

Node pro[204][204],maze_path[204];  //pro[][]记录某点的前趋结点,maze_path[]记录迷宫最短路径的的各点

typedef struct Queue_node  //队列结构体
{
    Node node;   //类型为Node结构体
    struct Queue_node *next;	
}Queue_node;

typedef struct Queue
{
	Queue_node *front;
	Queue_node *rear;
}Queue;

还有main函数

int main(void)
{
	ios::sync_with_stdio(false);
	int num;   //样例的大小
	cout << "输出一个整数代表要输入的测试例子个数:" ;
	cin >> num;    //输入样例的数量
	cout << endl;
	int k = 1;
    while(num--)
	{
		cout << "测试" << k << ":" << endl;
		k++;
		srand((unsigned)time(NULL)); //为了防止随机数每次重复，使用系统时间来初始化
		cout << "    输入整数M和N，用空格隔开，代表行数和列数，即表示迷宫的大小：";

		int M,N;  //表示迷宫为M*N矩阵
		cin >> M >> N; //输入

		if(M==0||N==0)
		{
			cout << endl;
			cout << "    警告!该数据无效，行数M和列数N必须不为0" << endl;
			continue;
		}
		cout << endl;
		int **maze = new int* [M+2];
		 for(int i=0; i<(M+2); i++)
		{

			maze[i] = new int [N+2];
		}

	    input(maze,M,N); //调用函数input(),选择输入方式，即选择自动生成还是手动输入数据
    
		int begin_end_type; 
    
		cout << "    请输入一个整数，0表示默认入口和出口的横纵坐标，1表示手动输入：";

		cin >> begin_end_type;

		cout << endl;

		int begin_x,begin_y,end_x,end_y; //入口横纵坐标，出口横纵坐标

		if(begin_end_type == 0) //如果该值为0，表示默认入口为左上角和出口为右下角
		{
			begin_x = 0;
			begin_y = 0;
			end_x = M-1;
			end_y = N-1;
		}
		else //如果等于1，表示手动定义入口和出口坐标
		{

			cout << "    请输入两个数，两个数用空格隔开，表示入口坐标(迷宫从第0行第0列开始):" ;
			cin >> begin_x >> begin_y ;
			cout << endl;
			cout << "    请输入两个数，两个数用空格隔开，表示出口坐标(迷宫从第0行第0列开始):" ;
			cin >> end_x >> end_y ;
			cout << endl;
			flag = 1;
		}
		int sum = 0; //记录从入口到出口的最短路径
		Queue queue;
		bfs(begin_x,begin_y,end_x,end_y,maze,sum,&queue,M,N); //;bfs搜索寻找最短路径

		int j =0;
		if(sum == -1)
		{
			cout << "    不能走出迷宫" << endl;
		}
		else
		{
			cout << "    能走出迷宫出口，最短路径为："<< sum << endl;
			cout << endl;
			cout <<"**************************按下任意键，结束本次测试**************************" ;
              cout << endl;

			print(begin_x,begin_y,end_x,end_y,j); //递归记录最短路径各点的坐标
			sum++;
		    image(sum,maze,M,N); //画最短路径图
		}

		fflush(stdin); //清空输入缓冲区

	}
    return 0;
}

3.1 如何记录bfs算法访问各个路径中点的横纵坐标

在bfs搜索迷宫时，对于当前遍历点po，如果下一个方向访问点newpoint满足在迷宫中、没有被访问过且为通路的条件，就将newpoint加入队列，定义一个数组pro保存newpoint的前驱点为po，代码为pro[newpoint.x][newpoint.y] = po。代码如下：

for(int i=0; i<8; i++)  //八个方向遍历
{
	newpoint.x = po.x + move_x[i];  //当前遍历点为po，newpoint为po的下一个方向
	newpoint.y=po.y + move_y[i];       	
	if(newpoint.x>=0&&newpoint.x<M&&newpoint.y>=0&&newpoint.y<N&&!visit[newpoint.x][new	point.y]&&maze[newpoint.x][newpoint.y]==0)
    {   
        //如果newpoint在迷宫中、没有被访问过、且为通路，就加入队列				 			
    	visit[newpoint.x][newpoint.y] = 1;  //将该点标记为已访问
    	newpoint.step = po.step + 1;      //该点的step为从起点到前一点po的step+1
    	pro[newpoint.x][newpoint.y] = po;  //记录该点的前趋点为po
    	EnQueue(newpoint,queue);    //将newpoint加入队列
    }
}

3.2 如何用VC6.0输出最短路径图

运用了easyx图形库，设置了窗口大小和字体画笔样式，设置了数据之间的间隔为50，将数据转化为字符输出。将maze_path数组保存的路径坐标依次用line函数连接成线，最后关闭绘图窗口。代码如下：

// #include <easyx.h> //图形库
// #include <TCHAR.H>   //easyx数字转字符
// #include <conio.h>//getch()函数头文件
void image(int &j,int **maze,int M,int N) //输出最短路径，画图
{
	initgraph(800,800,SHOWCONSOLE); //定义窗口大小,显示控制台
    settextcolor(WHITE); //设置画笔的颜色是白色
    settextstyle(20,0,"楷体"); //设置字体的样式
    int ox = 50;
	int oy = 50;
    for(int r=0; r<M; r++) //在屏幕中输出迷宫数据
    {
        for(int k=0; k<N; k++)
        {
			TCHAR tch = maze[r][k] + '0';  //将数组化为字符
			outtextxy(ox,oy,tch); //在屏幕中输出tch
            ox += 50;
        }
        oy += 50;
        ox = 50;
    }
    int width = textwidth(_T('1'))/2;  //获取文字的宽度
	int height = textheight(_T('1'))/2; //获取文字的高度
    for(int e=0; e<j-1; e+=1) 
    {
		//画圆圈
		circle((maze_path[e].y+1)*50+width,(maze_path[e].x+1)*50+height,15); 
		//画直线
		line((maze_path[e].y+1)*50+width,(maze_path[e].x+1)*50+height,(maze_path[e+1].y+1)*50+width,
(maze_path[e+1].x+1)*50+height);
    }
		circle((maze_path[j-1].y+1)*50+width,(maze_path[j-1].x+1)*50+height,15); //给最后一个数字画圆
    	getch();
    	closegraph(); //关闭绘图窗口
}

3.3 链式队列的基本操作

队列是计算机中一种常见的存储结构，具有先进先出的特点，既可从队头插入元素，也可在队尾插入元素，该课题采用的是尾插法。该课题的队列存储结构为链式队列，定义了头指针和尾指针。
（1）队列初始化。队列在使用前需要初始化，这里我定义了一个无头结点的链式队列，并对队列头指针和尾指针初始化为0，此时队列为空。代码如下：

void Init(Queue *q) //初始化队列，头指针和尾指针为空
{
    q->front = 0; 
    q->rear = 0;
}

（2）判断队列是否为空。定义函数类型为布尔型，如果队列为空则返回true，否则返回false。因为队列为空时头指针为0，所以当队头元素为空时即为q->front ==NULL。代码如下:

bool QueueEmpty (Queue *q)   //判断队列是否为空
{
	return (q->front == NULL); //当队列的队头元素为空时，队列为空
}

（3）入队。首先生成一个新结点，给结点的node成员赋值为入队元素no，如果此时，如果队列为空,则队列的头指针和尾指针都指向新生成的结点temp，否则更新尾指针

void EnQueue(Node &no,Queue *q)  //入队
{
	Queue_node *temp = new Queue_node();   //生成一个类型为Queue_node的新结点
    temp->node = no;   
    temp->next = NULL;
    if(q->front==NULL) //如果队列为空,则队列的头指针和尾指针都指向新生成的结点temp
    {
    	q->front = temp;
        q->rear = temp;
    }
    else //若队列不空，则更新尾指针
    {
        q->rear->next = temp;
        q->rear = temp;
    }
}

（4）出队。定义类型为Node结构体的出队函数DeQueue( )，声明一个类型为Node的变量n来保存队头元素的node属性。当队列只有一个元素时，出队后队列即为空，所以头指针和尾指针都要赋值为0。如果队列不止一个元素，则更新头指针指向下一个结点即可。接下来用delete回收队头元素，防止内存泄露。

Node DeQueue(Queue *q)  //出队列，取队头元素
{
    Node n = q->front->node;  //取出队头的node，即取出迷宫中保存某点的各信息，即x,y和step
    Queue_node  *que = q->front; //取出队头元素
    if(q->front == q->rear)  //如果队头元素等于队尾，即该队列只有一个元素，则出队时，头指针和尾指针都赋值为0
    {
        q->rear = 0;
        q->front = 0;
    }
    else      //否则更新头指针，指向下一个结点
        q->front = q->front->next;
    delete que; //回收队头元素
    return n; //返回迷宫结点
}

（5）销毁队列。t表示当前被删除回收的结点，tt表示被删除结点的下一个结点，当队列只剩一个结点时，头指针和尾指针都置空。

void DestroyQueue(Queue *q) //销毁队列
{
	Queue_node *tt = q->front; //取出队头元素
	Queue_node *t;
	while(tt!=q->rear) //当前元素不等于队尾时
	{
		t = tt; 
		tt = tt->next; //更新下次被删结点
		delete t;//回收元素
	}
	q->front = NULL;
	q->rear = NULL;
}

3.4 宽度优先搜索算法

宽度优先搜索又称广度优先搜索，简称bfs算法，是最简便的图的搜索算法之一，目的是系统地展开并检查图中的所有节点。bfs运用最多的地方就是求迷宫的最短路径，而bfs依靠队列的实现。

对于起点和终点，如果任意一方为墙，既值为‘1’，则无法走出迷宫。因此可以在搜索前进行条件判断，如果确定无法走出迷宫，则退出bfs函数。

接下来调用队列初始化函数Init( )，定义二维数组visit[ ][ ]记录某点是否已被访问，初始化全为0，如果被访问则值更新为1。将起点加入队列后，要标记visit[bx][by]为1。我们的迷宫允许可以有上、下、左、右、左上、左下、右上、右下八个方向可以走，所以设置了两个数组分别记录横纵坐标的变化值，分别是move_x[ ]和move_y[ ]。比如当数组move_x的某个值为1，move_y的值为1时，那么当前访问点的横纵坐标分别加上move_x和move_y即可表示为右下方向的点。

对起点的各个方向点进行条件判断，此时起点是前驱点，如果该方向点是通路、之前被访问过而且属于迷宫中的点时，则加入队列并用数组visit[ ][ ]标记为1，更新经过该点时的步数为前驱点的步数加一，并用数组pro[ ][ ]记录该方向点的前驱点信息，以便最终能找出最短路径中的各点。不断循坏，直到该前驱点的八个方向全部搜完，判断队列是否为空，如果为空，说明已没有路可走，即退出while循坏。如果此时队列非空，说明还有路可走，还有路可以去搜索。将队列的队头元素取出来，需要注意的是，如果队头元素是终点，说明我们已经找到了一条路径能通往终点的路，此时退出循坏。如果此时队头还不是终点，意味着任务还没完成，继续进行同样的八个方向搜，满足条件的方向点加入队列标记为访问等。在退出循坏后，我们得到一个变量sum的值，这个值记录了从起点到终点的路径，如果值为-1，代表“不能走出迷宫”，否则数值为最短路径的步数。

代码如下：

void bfs(int bx,int by,int ex,int ey,int **maze,int &sum,Queue *queue,int M,int N)//传入入口和出口坐标
{
	int move_x[] = {-1,1,0,0,-1,1,1,-1};   //八个方向的x和y
	int move_y[] = {0,0,1,-1,1,-1,1,-1};
    if(maze[bx][by]==1 || maze[ex][ey]==1) //如果起点或终点中有一个是墙，则无法走出迷宫
    {
        sum = -1;   //sum为-1时代表“无法走出迷宫”
        return ;    
    }
    sum = -1;
	Init(queue);			//初始化队列
    Node point,newpoint;	//声明两个结构体
	int visit[204][204];   //数组visit记录某点是否已访问
    memset(visit,0,sizeof(visit));	//初始化两个数组为0
    memset(pro,0,sizeof(pro));
    visit[bx][by] = 1;		//访问入口起点，赋值为1
    point.x = bx;			//记录起点信息
    point.y = by;
    point.step = 0;
    EnQueue(point,queue);		//将起点加入队列
    while(!QueueEmpty(queue))		
    {
        Node po = DeQueue(queue);		//取出队头的结构体
        if((po.x == ex) && (po.y == ey))	//如果队头为终点，退出bfs
        {
            sum = po.step;   //sum记录从起点到终点的最短路径
            return ;
        }
        for(int i=0; i<8; i++)  //八个方向遍历
        {
            newpoint.x = po.x + move_x[i];  //当前遍历点为po，newpoint为po的下一个方向
            newpoint.y = po.y + move_y[i]; 
            if(newpoint.x>=0&&newpoint.x<M&&newpoint.y>=0&&newpoint.y<N&&!visit[newpoint.x][newpoint.y]&&maze[newpoint.x][newpoint.y]==0)
            {   //如果newpoint在迷宫中、没有被访问过、且为通路，就加入队列
                visit[newpoint.x][newpoint.y] = 1;  //将该点标记为已访问
                newpoint.step = po.step + 1;      //该点的step为从起点到前一点po的step+1
                pro[newpoint.x][newpoint.y] = po;  //记录该点的前趋点为po
                EnQueue(newpoint,queue);    //将newpoint加入队列
            }
        }
    }
    DestroyQueue(queue); //销毁队列
}

3.5 递归保存最短路径中点的坐标

代码如下：

void print(int bx,int by,int xx,int yy,int &j) //从终点位置开始递归，xx和yy表示当前访问的横纵坐标
{
    if((xx==bx) && (yy==by)) //如果当前访问地点为起点位置，返回退出
    {
        maze_path[j].x =xx, maze_path[j].y = yy;
        j++;
        return ;
    }
    else
    {
        print(bx, by, pro[xx][yy].x, pro[xx][yy].y, j);
        maze_path[j].x = xx,maze_path[j].y = yy; //记录第j个点的横纵坐标
        j++;
    }

}

4、实验截图

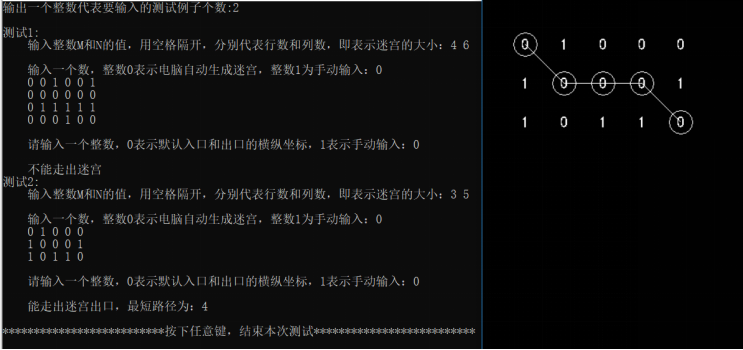
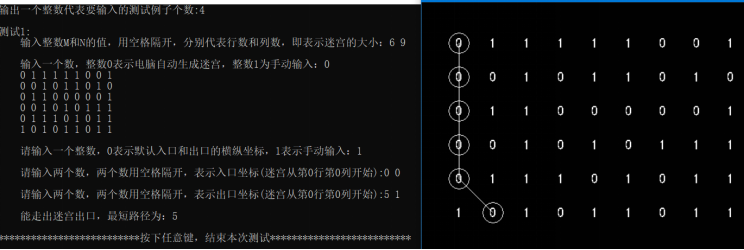
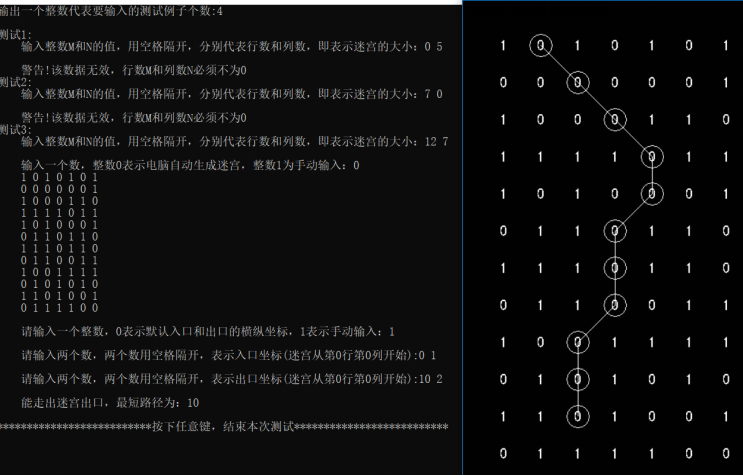
在这里插入图片描述在这里插入图片描述

在这里插入图片描述

1/9更新，全部代码都放这了，已经和百度网盘里面的文件差不多了
我太感动了，居然还有两个人收藏，谢谢你们~
欢迎指出不足之处噢~

在这里插入图片描述

最后

以上就是任性唇膏为你收集整理的利用easyX图形库画迷宫问题的路径前言的全部内容，希望文章能够帮你解决利用easyX图形库画迷宫问题的路径前言所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(47)

相关文章

C语言在坐标轴上输出曲线,用Flash与C语言制作工程实时数据动态曲线图
C语言在坐标轴上输出曲线,用Flash与C语言制作工程实时数据动态曲线图
【C#语言】绘制两条折线图
【C#语言】绘制两条折线图
easyx时钟
easyx时钟
python打开csv文件绘制折线图_Python入门--利用matplotlib导入csv数据绘制折线图（2）...
python打开csv文件绘制折线图_Python入门--利用matplotlib导入csv数据绘制折线图（2）...
利用easyX图形库画迷宫问题的路径前言
利用easyX图形库画迷宫问题的路径前言
Easyx介绍与安装Easyx介绍与安装
Easyx介绍与安装Easyx介绍与安装
Easyx 函数集合:
Easyx 函数集合:
fillcircle
fillcircle

评论列表共有 0 条评论

立即
投稿
返回
顶部